🌥️ 📅 😵 洗練されたデザインについて 💆 💠 👨‍🚒

はじめに

このエレガントなデザインにどのように慣れたのかを説明することから、記事を始めます。オリンピアードのプログラミングを追求して、先生と私は多くの興味深い問題を解決しました。そしてある日、次のタスクに出くわしました。

分母がnを超えないすべての既約分数を昇順で出力します（n <= 100）。

問題の状態を最後まで読んだとき、それは私には複雑に見えませんでした（そうではありません）。私が最初に思いついたのは、分子と分母が相互に単純であれば、2からnまでのすべての分母を単純に整理し、各分母について分子を1から分母まで反復することでした。それでは、昇順に並べ替えてください。

このソリューションは正しく、タスクはそれに割り当てられたすべてのテストに合格しました。しかし、私の先生は、この問題はもっと美しく解決できると言っていました（彼はすでにこの設計に遭遇しています）。だから私はこの素晴らしいデザインに精通しました-Stern-Brocoツリー。

スターン・ブロコの木

Stern-Brocoツリーは、ドイツの数学者Meritz Sternとフランスの時計メーカーAchilles Brocoによって独立して発見されました。このツリーを使用すると、すべての既約、非負の分数のセットを構築できます。

まず、次の用語を導入します 。2つの分数を与えます

。その後、分数

- 中央値と呼ばれます。

2つの架空の部分からツリーの構築を開始します。

-0を示します。

-無限を「既約形式で」示します。

後続の各反復で、それらの中央値が挿入される分数の間に、結果の分数のペアのそれぞれに対して同じ操作が繰り返されます。

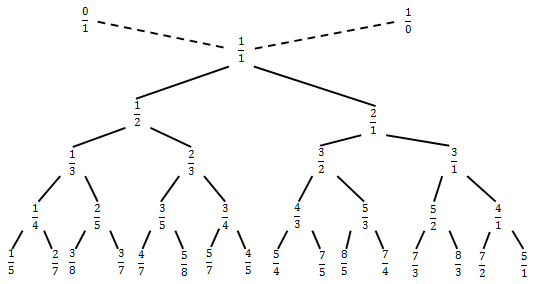
このプロセスを無限に続けると、既約で非負の分数の集合全体を構築できます。

Stern-Brocoツリーは、すばらしい機能がなければそれほど興味深いものではなく、多くの機能を備えています。

分数の既約;
分数の順序付け;
絶対にすべての画分の存在。

1つは尋ねるかもしれません：なぜすべての分数が既約なのですか？なぜ注文されたのですか？なぜ単一のフラクションが複数回会うことができないのですか？これらの質問に対する答えは非常に簡単です。このツリーの構造を検討するには、もう少し詳細が必要です。

させて

-Stern-Brocoツリーの2つの連続した部分。等式yz-xt = 1がそれらに当てはまることに気付くかもしれません（分数のペアについてはこれを自分で確認してください）ツリー内のすべての分数について帰納法によりこのステートメントを証明します。帰納法の基礎として、分数を取ります

そして

等式1 * 1-0 * 0 = 1は真です。

ここで、分数間に中央値を挿入するとき、

等式yz-xt = 1が真である場合、分数も保持されます

。

私たちが持っています：

ご覧のとおり、これらの方程式は両方とも元の方程式と同等であるため、条件yz-xt = 1-は、ツリー内のすべての連続した分数に対して不変です。条件yz-xt = 1はどういう意味ですか？つまり、GCD（x、y）= GCD（z、t）= 1です。実際、数値x、yおよびz、tは互いに素です（GCD（x、y）≠1の場合、左側はGCDで除算されます、ただし、GCD（z、t）の場合と同様に、右側は1だけで除算されます。

そのため、分数は既約であり、分子と分母は常に相互に単純です。彼らは最初の質問に答えました！ 2回目に通ります！

なぜ分数が注文されるのですか？この質問に答えるには、2つの分数の中央値が常にそれらの間にあることを示すだけで十分です。

させて

-ツリー内の2つの連続した分数

。それを示す

。分数を共通分母にし、条件を考慮する

私達は得る：

最後の分数の分母が正である場合、分子は負でなければならず、これは元の不等式xt-yz≤0です。このことから、2つの分数の中央値は常にそれらの間にあると結論付けられます（必ずしも中間にあるとは限りません）。したがって、Stern-Brocoツリーの分数の順序を示しました。

さて、最後の1つです！なぜ少なくとも1つの分数を見逃してはならないのか、つまり、なぜすべての分数がツリーに存在するのか？

ツリー内の特定の部分を見つける必要がある場合、どのようにそれを行うのでしょうか？検索プロセスは、実際にはバイナリ検索です。希望の割合を中央値と比較し、3つのケースが可能です。

中央値に等しい場合、検索は完了します。
中央値が分数よりも大きい場合、左のサブツリーを調べるために再帰的に開始します。
中央値が分数よりも小さい場合、再帰的に開始して正しいサブツリーを検索します。

明らかに、このプロセスは無期限に実行することはできません。したがって、いつか私たちは分数を見つけます（なぜそうなのかを自分で考えてください） 。

ファレイ配列

さて、元のタスクはどうですか？ Stern-Brocoツリーは私たちに適しているように見えますが、余分な大きなユニットの一部が含まれています。ただし、架空の分数の代わりに使用できないのは何ですか

そして

分数

？何もない！

Stern-Brocoツリーのこのような特殊なケースは、Fareyシーケンスの基礎です。

次数nのFareyシーケンスは、分母がnを超えない0から1までのすべての既約分数のセットであり、昇順に配置されます。シーケンスは、文字F _nで示されます。

厳密に数学的には、このシーケンスは次のように記述できます。

これは、n = 1、...、5のFareyシーケンスの方法です。

このシーケンスは、有名な地質学者のジョン・ファレイにちなんで命名されました。

実際、元の問題は次のように再定式化できます。n次のFareyシーケンスを構築します。その構築のためのC＃コードは非常に単純に見え、2つの再帰呼び出しのみです。

public static void FareiSequence(int n) { Console.WriteLine("{0} / {1}", 0, 1); FareiSequence(n, 0, 1, 1, 1); Console.WriteLine("{0} / {1}", 1, 1); } private static void FareiSequence(int n, int x, int y, int z, int t) { int a = x + z, b = y + t; if (b <= n) { FareiSequence(n, x, y, a, b); Console.WriteLine("{0} / {1}", a, b); FareiSequence(n, a, b, z, t); } }