それで、あなたはまだHindley-Milnerを理解していませんか？ パート2

パート1では 、Hindley-Milner形式化に必要な構成要素について説明しました。この投稿では、それらの定義を指定し、形式化全体を定式化します。

表現の概念の形式化

式が何であるかを再帰的に定義します。 つまり、ほとんどのタイプの式を定義し、既存の式に基づいてより複雑な新しい式を作成する方法を説明し、有効な式のみがこの方法で作成できることを示します。

1. 変数は有効な式です。
2. e
   
   
   
   が任意の式であり、 x
   
   
   
   が任意の変数である場合、 λx.e
   
   
   
   は式です。 e
   
   
   
   をx
   
   
   
   を含む通常の（必ずしもではないが）複雑な式と考えるのに役立ちます。 x² +2
   
   
   
   、次にx
   
   
   
   を入力として受け取り、 x
   
   
   
   特定の値について式e
   
   
   
   を評価した結果を返す匿名関数として約λx.e
   
   
   
   簡単に言えば、と考えてください
   
   

    function(x) { return x^2 + 2; }
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

3. f
   
   
   
   とe
   
   
   
   が有効な式である場合、 f(e)
   
   
   
   も有効です。 明らかな理由から、 アプリケーションと呼ばれます 。
4. x
   
   
   
   が変数であり、 e
   
   
   
   ₁およびe
   
   
   
   ₀が有効な式である場合、 e
   
   
   
   ₀でのx
   
   
   
   各出現をe
   
   
   
   ₁で置き換えると、有効な式も得られます。 つまり、たとえば、 e
   
   
   
   ₁ = x² +2
   
   
   
   およびe
   
   
   
   ₀ = y/3
   
   
   
   場合、 x
   
   
   
   = e
   
   
   
   ₀をe
   
   
   
   ₁に設定すると、式(y/3)
   
   
   
   ² +2
   
   
   
   ます。
   
   [注：最後の段落は冗長であり、式のラムダ計算の定義に公式には含まれていません。e1でe
   
   
   
   ₀をx
   
   
   
   に置き換えることは、抽象化λx.
   
   
   
   を適用すること_と同等λx.



e
   
   
   
   ₁からe
   
   
   
   ₀ 。 いわゆるlet-polymorphismをサポートするためにのみ追加されます。]

これ以上受け入れられる表現はありません。



余談です。この問題に十分な注意を払っている人は誰でも驚かれるでしょう。「ちょっと待ってください。どうすれば有用な表現ができますか？」 上記のみに基づいてx



² +2



（または少なくとも2）を取得するにはどうすればよいですか？ くそー、ゼロはどうですか？ これらのルールには、明らかに式0につながる行はありません。 この場合の解決策は、ラムダ計算で式を作成することです。ラムダ計算は、正しい解釈で0,1、...、+、×、-、/のように動作します。 つまり、数値、算術演算、文字列などをエンコードする必要があります。 ラムダ構文を使用して作成できるパターンに変換します。 この投稿には、数値と算術演算に関する小さいながらも非常に優れたセクションがあります。 これはラムダ計算の興味深い機能です：単純な4つのポイントで再帰的に定義できる基本的な構文がありますが、言語自体に数値、文字列、すべての型を記述する表現力があるため、4つの主要なステップで多くのことを帰納的に証明できます必要な操作。

型要求の形式化

e



を「 e



」がメタ言語の変数であるような式とすると、ベース言語の式を示します。 たとえば、次のいずれかです。

 x Math.pow(x,2) [1,2].forEach ( function(x) { print(x); } )
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、 t



が任意の型である場合、「 e



has type t



」を次のように表現できます。

e:t







e



と同様に、 t



はメタ言語の変数であり、ベース言語の任意の型（Int、Stringなど）に一致します。 そして、 e



場合と同様に、 t



特定のタイプのマッチングはオプションです。



式について上記で行ったように、型と見なされるものの正式な定義を与えることもできます。 ただし、この場合の抽象化はかなり複雑なので、この瞬間は省略します。 念頭に置いて、次の2つの重要なポイントに注目してください。

1. s
   
   
   
   とt
   
   
   
   がタイプの場合、 t
   
   
   
   → s;
   
   
   
   入力にt
   
   
   
   があり、出力にs
   
   
   
   がある関数のタイプ
2. r
   
   
   
   が他の型で構成されている可能性があるタイプ（ t
   
   
   
   → s
   
   
   
   がt
   
   
   
   とs,
   
   
   
   構成されている方法に似ておりs,
   
   
   
   それぞれが他のいくつかの型の構成として潜在的に表される場合）、およびα
   
   
   
   がこの型の変数である場合、 α.r
   
   
   
   はタイプです。
   
   例がなければ、上記はやや無意味に聞こえます：
   
   

    function (x) { return x; }
         
         
   
           
           
           
         
   
       
           
           
           
         
         
   
           
           
           
         
   
       
        

   
   
   この関数のタイプはString
   
   
   
   → String
   
   
   
   です。 またはInt
   
   
   
   → Int
   
   
   
   。 実際、タイプt
   
   
   
   、そのタイプはt
   
   
   
   → t
   
   
   
   です。 タイプtt
   
   
   
   → t
   
   
   
   と言います。 String
   
   
   
   → String
   
   
   
   またはt
   
   
   
   → t
   
   
   
   各タイプは「モノタイプ」です。 tt
   
   
   
   → t
   
   
   
   は「ポリタイプ」です。 上記の関数と同一の関数は、抽象ポリタイプtt
   
   
   
   → t
   
   
   
   を持ちます。これは、実際には、任意の実際の型t
   
   
   
   に対して、型t
   
   
   
   → t
   
   
   
   持つことを意味します。 上記のすべてをまとめると、このようなコンパクトな要約レコードが得られます。
   
   α.α



xx:



α.α
   
   
   
   → α
   
   
   
   

型要求の形式化

ここで、特定の表現とそのタイプの知識から、より多くの表現のタイプの派生に移行する方法に関するルールのブランチを形式化します。 文計算がModus Ponensをどのように定式化したか覚えていますか？ 同様のことを行います。 たとえば、引数の次の部分を形式化するとします。

duck



変数のタイプがAnimal



あるとすでに推測できるとします。

さらに、 speak



はAnimal-> String



型のメソッドであると推測したとします。

それから、 speak(duck)



はString



型であると推測できます。



そして、この形式に適合する推論は、有効な型推論です。

これを次のように形式化します。





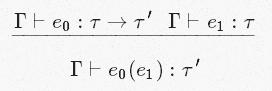
このルールは[App]（オーバーレイ用）と呼ばれ、StackOverflowのこの質問に存在するルールの1つです。 彼と残りのルールについては、次の投稿で説明します。 それまでの間、上で出会ったすべてのシンボルを把握しましょう。

• Γ-私たちがすでに知っている、またはおそらく仮定できる位置のセットに対応します。 より一般的には、Γは（式とそのタイプに関する）ステートメントのコレクションの単なる反映です。 そして当然、文字Γについて特別なことは何もありません-ギリシャ語の大文字は、しばしば位置のセットを指すために使用されます。
• ⊢-「ターンスタイル」、つまり何かを引き出すことができることを意味します。 たとえば、Γ⊢x x:t
  
  
  
  は、仮定/公理/既存の知識としてΓからステートメントを取得した場合、 x
  
  
  
  がt
  
  
  
  型でt
  
  
  
  と推定できることを意味します。
• ε-「イプシロン」、何かに属することを意味します。 x:t
  
  
  
  t∈Γは、ステートメントx:t
  
  
  
  がΓに属することを意味します。
• その長い水平線。 この行は、分子を初期前提とする場合、分母にある結論を引き出すことができることを示しています。 これにより、「これとこれを導き出すことができれば、これとそれも引き出す​​ことができます」のようなことを表現できます。 例：
  
  
  
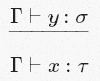
  y
  
  
  
  がΓからσ型であると推定できる場合、 x
  
  
  
  はΓからτ型であると推定できます。

次のステップ：

• パート3では、すべてをまとめて、HMアルゴリズムで使用されるルールのアイデアを取得します。

翻訳者のメモ：翻訳に関するPMのコメントに非常に感謝します。