

この記事では、擬似コードとMatlabコードを使用したアルゴリズムの操作について説明します。 私が英語で書いたオリジナルの記事はgithubのソースコードでここにあります 。
画像エネルギー
プレゼンテーションを簡素化するために、画像のサイズを縮小する場合のみを説明します。 画像の拡大も同様のプロセスです。
アルゴリズムの考え方は、ユーザーにとって重要度の低い(情報が少ない)コンテンツを削除することです。 この情報の測定値を「エネルギー」と呼びます。 このような関数として、空間l1の画像勾配を使用できます。
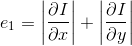
画像に3つのチャネルがある場合、画像全体の勾配として、各チャネルの勾配の合計を使用します。 以下のmatlabコードは、このアプローチを示しています。
function res = energyRGB(I) % returns energy of all pixelels % e = |dI/dx| + |dI/dy| res = energyGrey(I(:, :, 1)) + energyGrey(I(:, :, 2)) + energyGrey(I(:, :, 3)); end function res = energyGrey(I) % returns energy of all pixelels % e = |dI/dx| + |dI/dy| res = abs(imfilter(I, [-1,0,1], 'replicate')) + abs(imfilter(I, [-1;0;1], 'replicate')); end
そして、これは、使用された画像にエネルギー関数を適用した結果がどのように見えるかです:

縫い目
最小エネルギーで任意の位置のピクセルを削除すると、画像が破損します。 最小限のエネルギーで列/列を削除すると、不要なアーティファクトが表示されます。 ここでは、列ごとに、{(i、j)| jは固定されています}、列{(i、j)| 修正しました}。 ジレンマの解決策は、列/列の概念の一般化を導入することです。
正式には、nxmイメージにして、垂直シームを呼び出します
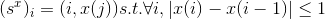 、
、
ここで、x:[1、..、n]-> [1、..、m]。 つまり、垂直シームは画像の上部から下部へのパスであるため、パスの長さは画像の幅であり、シームに属する各要素(i、j)について、次の要素は(i + 1、j-1)、(i +1、j)、(i + 1、j +1)。 同様に、水平シームを導入できます。 垂直および水平シームの例を以下に示します。

最小限のエネルギーの縫い目に興味があります
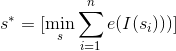
このような継ぎ目を見つけるには、動的プログラミングを使用します。
- 各(i、j)のすべての可能な継ぎ目に対する最小エネルギーの行列Mを見つける:
- 最初の行Mをエネルギー行列eの値で埋めます
- 2番目から始まるすべての行について:
M [i、j] = e [i、j] + min(M [i-1、j]、M [i、j]、M [i +1、j]);
- マトリックスMの最後の行で最小値を見つけ、このピクセルから最初の行までのパスを作成し、各ステップで最小エネルギーのピクセルを選択します(同様に(i、j)について、位置[i-1、j]、[i 、j]、[i + 1、j])。
効率上の理由から、Matlabコードではnxmビットマトリックスを使用してシームを表します。 ピクセルがシームに属する場合、ラベルは0になり、そうでない場合は1になります。
function [optSeamMask, seamEnergy] = findOptSeam(energy) % finds optimal seam % returns mask with 0 mean a pixel is in the seam % find M for vertical seams % for vertical - use I` M = padarray(energy, [0 1], realmax('double')); % to avoid handling border elements sz = size(M); for i = 2 : sz(1) for j = 2 : (sz(2) - 1) neighbors = [M(i - 1, j - 1) M(i - 1, j) M(i - 1, j + 1)]; M(i, j) = M(i, j) + min(neighbors); end end % find the min element in the last raw [val, indJ] = min(M(sz(1), :)); seamEnergy = val; optSeamMask = zeros(size(energy), 'uint8'); %go backward and save (i, j) for i = sz(1) : -1 : 2 %optSeam(i) = indJ - 1; optSeamMask(i, indJ - 1) = 1; % -1 because of padding on 1 element from left neighbors = [M(i - 1, indJ - 1) M(i - 1, indJ) M(i - 1, indJ + 1)]; [val, indIncr] = min(neighbors); seamEnergy = seamEnergy + val; indJ = indJ + (indIncr - 2); % (x - 2): [1,2]->[-1,1]] end optSeamMask(1, indJ - 1) = 1; % -1 because of padding on 1 element from left optSeamMask = ~optSeamMask; end
水平シームを見つけるには、転置エネルギー行列をfindOptSeam関数に渡すだけです。
最高の縫い目除去順序を見つける
そのため、最小の継ぎ目を見つけることができ、以下のコードを使用して画像から削除できます。
function [optSeamMask, seamEnergy] = findOptSeam(energy) % finds optimal seam % returns mask with 0 mean a pixel is in the seam % find M for vertical seams % for vertical - use I` M = padarray(energy, [0 1], realmax('double')); % to avoid handling border elements sz = size(M); for i = 2 : sz(1) for j = 2 : (sz(2) - 1) neighbors = [M(i - 1, j - 1) M(i - 1, j) M(i - 1, j + 1)]; M(i, j) = M(i, j) + min(neighbors); end end % find the min element in the last raw [val, indJ] = min(M(sz(1), :)); seamEnergy = val; optSeamMask = zeros(size(energy), 'uint8'); %go backward and save (i, j) for i = sz(1) : -1 : 2 %optSeam(i) = indJ - 1; optSeamMask(i, indJ - 1) = 1; % -1 because of padding on 1 element from left neighbors = [M(i - 1, indJ - 1) M(i - 1, indJ) M(i - 1, indJ + 1)]; [val, indIncr] = min(neighbors); seamEnergy = seamEnergy + val; indJ = indJ + (indIncr - 2); % (x - 2): [1,2]->[-1,1]] end optSeamMask(1, indJ - 1) = 1; % -1 because of padding on 1 element from left optSeamMask = ~optSeamMask; end
この一連の操作は、重要な詳細を維持しながら、画像の幅または高さのサイズを変更するのに十分です-必要な水平シームと垂直シームの数を削除するだけです。
しかし、画像のサイズを縦横に同時に縮小する必要がある場合はどうでしょうか? 各反復でエネルギーを最小化するという点で何が良いかを理解する方法-垂直の継ぎ目または水平を削除するには?
この問題は、動的プログラミングを使用して再び解決できます。 n 'とm'を希望の画像サイズ(n '<n、m' <m)とします。 マトリックスTを導入します。このマトリックスは、各n 'x m'に対して、垂直シームと水平シームを削除する最適なシーケンスのコストを決定します。 便宜上、r = n-n '、m = m-m'を導入します。これは、垂直方向と水平方向の除去の数を表します。 Tに加えて、サイズrxcのTBMマトリックスを導入します。これは、T(i、j)が垂直(1)または水平(0)の継ぎ目を削除してT(i、j)に到達したかどうかに応じて、T(i、j)ごとに0または1を格納します。 擬似コードは次のとおりです。
- T(0、0)= 0;
- 境界でTの値を初期化します。
すべてのj {
T(0、j)= T(0、j-1)+ E(海上);
}
すべてのi {
T(i、0)= T(j-1、0)+ E(水平の縫い目);
}
- 境界でTBM値を初期化します。
すべてのj {T(0、j)= 1; }
すべてのi {T(0、i)= 0; }
- TとTBMを入力します。
for i = 2 to r {
imageWithoutRow = image;
j = 2からc {
energy = computeEnergy(imageWithoutRow);
horizontalSeamEnergy = findHorizontalSeamEnergy(エネルギー);
verticalSeamEnergy = findVerticalSeamEnergy(エネルギー);
tVertical = T(i-1、j)+ verticalSeamEnergy;
tHorizontal = T(i、j-1)_ horizontalSeamEnergy;
if(tVertical <tHorizontal){
T(i、j)= tVertical;
transBitMask(i、j)= 1
} else {
T(i、j)= t Horizontal;
transBitMask(i、j)= 0
}
//左から右に移動-垂直シームを削除
imageWithoutRow = removeVerticalSeam(エネルギー);
}
エネルギー= computeEnergy(イメージ);
image = removeHorizontalSeam(エネルギー);
}
- T(r、c)からT(1、1)へのパスを見つけ、TBM(i、j)の値に応じて行または列を削除します。
Matlabでの実装:
function [T, transBitMask] = findTransportMatrix(sizeReduction, image) % find optimal order of removing raws and columns T = zeros(sizeReduction(1) + 1, sizeReduction(2) + 1, 'double'); transBitMask = ones(size(T)) * -1; % fill in borders imageNoRow = image; for i = 2 : size(T, 1) energy = energyRGB(imageNoRow); [optSeamMask, seamEnergyRow] = findOptSeam(energy'); imageNoRow = reduceImageByMask(imageNoRow, optSeamMask, 0); transBitMask(i, 1) = 0; T(i, 1) = T(i - 1, 1) + seamEnergyRow; end; imageNoColumn = image; for j = 2 : size(T, 2) energy = energyRGB(imageNoColumn); [optSeamMask, seamEnergyColumn] = findOptSeam(energy); imageNoColumn = reduceImageByMask(imageNoColumn, optSeamMask, 1); transBitMask(1, j) = 1; T(1, j) = T(1, j - 1) + seamEnergyColumn; end; % on the borders, just remove one column and one row before proceeding energy = energyRGB(image); [optSeamMask, seamEnergyRow] = findOptSeam(energy'); image = reduceImageByMask(image, optSeamMask, 0); energy = energyRGB(image); [optSeamMask, seamEnergyColumn] = findOptSeam(energy); image = reduceImageByMask(image, optSeamMask, 1); % fill in internal part for i = 2 : size(T, 1) imageWithoutRow = image; % copy for deleting columns for j = 2 : size(T, 2) energy = energyRGB(imageWithoutRow); [optSeamMaskRow, seamEnergyRow] = findOptSeam(energy'); imageNoRow = reduceImageByMask(imageWithoutRow, optSeamMaskRow, 0); [optSeamMaskColumn, seamEnergyColumn] = findOptSeam(energy); imageNoColumn = reduceImageByMask(imageWithoutRow, optSeamMaskColumn, 1); neighbors = [(T(i - 1, j) + seamEnergyRow) (T(i, j - 1) + seamEnergyColumn)]; [val, ind] = min(neighbors); T(i, j) = val; transBitMask(i, j) = ind - 1; % move from left to right imageWithoutRow = imageNoColumn; end; energy = energyRGB(image); [optSeamMaskRow, seamEnergyRow] = findOptSeam(energy'); % move from top to bottom image = reduceImageByMask(image, optSeamMaskRow, 0); end; end
おわりに
このアルゴリズムは、風景画像でうまく機能します。アルゴリズムがダイナミクスでどのように機能するかを示すgifを参照してください( sharaに感謝)。

しかし、そのままでは、詳細に満ちたポートレートや画像にはあまり適していません。 風景画像では、空または海にはほとんど情報が含まれておらず、画像は通常、それらのために縮小されます。 多くの小さな詳細を含む画像を撮影した場合、アルゴリズムは最良の結果を提供しません(例はAvidan&A. Shamirの記事から取られています)。

ユーザーの参加なしでは、シームカービングをポートレート写真に適用すべきではありません。なぜなら、私たちにとって重要なオブジェクトである人物には、シームカービングの観点からの情報が少ないからです。

このアルゴリズムを使用して、マークされたオブジェクトを画像から削除できます(Avidan&A. Shamirの記事からの例です)。
