
エントロピーの概念は、科学技術のほぼすべての分野で使用されています。
ボイラー室の設計から人間の意識のモデルまで。
熱力学および動的システムと計算方法の両方の基本的な定義を理解することは難しくありません。 しかし、森の中に行くほど、-が増えます。 たとえば、私は最近、太陽エネルギーだけでなく、その低エントロピーが地球上の生命にとって重要であることを発見しました(R.ペンローズのおかげで、「現実への道」pp。592-593) 。
単純な動的システムまたは1次元データ配列(システムの動きの「トレース」として取得できる)に制限する場合、ランダム性の尺度としてエントロピーの少なくとも3つの定義をカウントできます。
それらの最も深く完全なもの(コルモゴロフシナイ)は視覚的に調べることができ、
プログラムの使用-ファイルアーカイバ。
はじめに
情報エントロピーに言及して、彼らはしばしばシャノンの「魔法」の公式を与えます:

ここで、Nは可能な実装の数、bは測定単位(2ビット、3トリット、..)、p i-実装の確率です。
もちろん、すべてがそれほど単純ではありません(しかし興味深い!)。 最初の(2番目、さらには3番目の)知り合いについては、A。Yaglom、I。Yaglomの「確率と情報」、1973年の古くなっていない本をお勧めします。
「子供の」質問への答えとして:「 式によって得られた数は何を意味するのか?」
このような鮮やかなイラストで十分でしょう。
N = 16個のセルがあり、そのうちの1つが十字でマークされているとします。
[] [] [] [] [] [] [] [] [] [] [] [x] [] [] [] []
選択はランダムです。 i番目のセルがラベル付けされる確率はp i = 1/16
シャノンのエントロピーは次と等しい
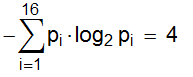
ゲームを想像してください。 1人のプレイヤーがセルを描画し、ダッシュし、2人目だけに伝えます
セルの数。 2つ目は、どのタグが付けられ、質問をするかを見つけることです。
しかし、最初の回答は「はい」または「いいえ」のみになります。
十字架がどこにあるのかを知るために、最低いくつの質問が必要ですか?
答えは「 4 」です。 そのようなすべてのゲームでは、質問の最小数は情報エントロピーに等しくなります。
どの質問をするかは問題ではありません。 適切な戦略の例は
セルを半分に分割し(Nが奇数の場合、1セルの過剰/欠乏で)、尋ねます:
「前半の十字架?」などで学んだので、それを半分に分けるなど。
別の種類の「素朴な」深い質問: シャノンの公式に対数があるのはなぜですか?
実際、対数関数とは何ですか? 逆指数関数...そして指数関数とは何ですか?
実際、厳密な定義は分析の過程で与えられますが、それらはまったく複雑ではありません。
しばしば「入力」を増やすと、「出力」は数単位だけ増えます。
オーギュスタン・コーシーは、方程式
f(xy)= f(x)+ f(y)x、y> 0
唯一の連続解があります。 これは対数関数です。
今、2つの独立した試験を実施していると想像してください。 彼らが持っている結果の数はnとmであり、それらはすべて同じ確率です(たとえば、サイコロとコインを同時に投げます; n = 6、m = 2)
明らかに、ダブルエクスペリエンスの結果の数は、製品n・mに等しくなります。
実験の不確実性は合計されます。 そして、この不確実性の尺度としてのエントロピーは、
条件h(mn)= h(m)+ h(n)を満たします。 対数である。
コルモゴロフシナイのエントロピー
この基本概念の厳密な定義を理解することは非常に困難です。
彼に徐々に近づきます。
「位相空間」は自然数の1次元配列になります。
たとえば、数値「Pi」の10進数:{3、1、4、1、1、5、9、2、6、...}
実際、あらゆる種類のデータ(もちろん損失を伴う)をこのフォームに持ち込むことができます。
値の範囲全体をN個の間隔に分割し、k番目の間隔に入る場合は、数値kを書き留めます(サウンドサンプリングの場合と同様)。
これまたはそのシーケンスはどの程度ランダムまたは確率的ですか?
もちろん、情報エントロピーは「カオスメーター」の良い候補です。
異なる数の出現の確率がすべて等しい場合に最大であることを証明するのは簡単です。
しかし、その後、私は以前の投稿で言及した困難が始まります。
たとえば、配列... 01010101010101010101 ...には最大エントロピーがあり、0と1の最小ランダムシーケンスです。
データが最初はデジタル(音声、写真)ではない場合、さまざまな方法でデータを0からNの数値に変換できます。 また、数値配列の確率は、個々の要素だけでなく、ペア、トリプル、奇数などについても測定できます。
さて、多くのオプションがあるので、 それらすべてを使用します!
さまざまな数体系、ペアやトリプルへの分割など、あらゆる方法で「実験」配列を表示します。 明らかに、そのサイズLとシャノンエントロピーHはマッピング方法に依存します。
たとえば、それを積分不可能なオブジェクトと考えると、L = 1、H = 0になります。
HがLの増加とともに成長することを考えると、量を導入します

これは、コルモゴロフ-シナイエントロピーの(やや単純化された)定義です( 厳密な定義です)。 理論的な意味では、完璧です。
しかし、技術的には、すべてのパーティションの上限を見つけることは非常に困難です。 さらに、明確にするために、すべての結果を整然と整理する必要があり、これは別の重大なタスクです。
幸いなことに、理論の厳密さをほとんど弱めないアプローチがありますが、はるかに視覚的であり、
実用的。
アーカイブとエントロピー
Habréでの情報圧縮の方法とアルゴリズムについて複数回語られましたが、
habrahabr.ru/post/142242
habrahabr.ru/post/132683
元のソースは言うまでもありません。
かつては、完全に回復して50%に圧縮する能力が衝撃的な印象を与えました。
データ圧縮の程度とそれらのコルモゴロフ-シナイエントロピーとの関係が厳密に証明されていることを知ったとき、私は最近も驚きませんでした。 直観的には、これは理解できます。データの順序が整うほど、圧縮エンコードの機会が増えます。
しかし、厳密な数学的考察は必ずしも「常識」を確認するものではありません。
この主題に関する記事はかなり複雑ですが ( 主なものも有料です)、理論家はすべてが合法であると信じ、実験に進みます。
4種類のデータを作成します。
- piの10進数(π)
- PRNG Wolfram Mathematica(ランダム)
- 決定的カオスの最も明るくシンプルな例はロジスティックマッピングです
- 1つの「1」の配列(定数)
- 一見しただけで乱数を生成するグリッチ式の一種(マップ)
もちろん、シャノンの式(Mathematicaにエントロピー[]として組み込まれている)を使用してエントロピーを計算できます。
ただし、前述のように、結果は数値システム、データ表示の形式などに大きく依存します。
たとえば、これは、増え続けるデータのロジスティックエントロピーのグラフです。
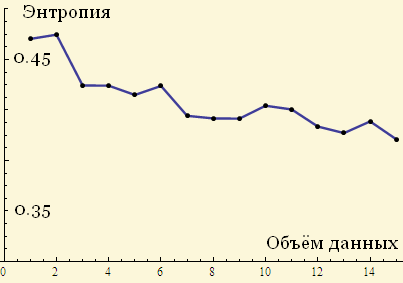
エントロピーが配列のサイズの増加に伴って特定の値になる傾向があるかどうかはあまり明確ではありません。
次に、圧縮を使用してエントロピーを測定してみましょう。 各例について、異なるサイズの配列を作成し、配列の長さに応じて「圧縮後のサイズ/圧縮からサイズへ」の関係グラフを作成します(正直、WinRARヘッダーの代わりに組み込みのzip zipアーカイバーを使用しました)
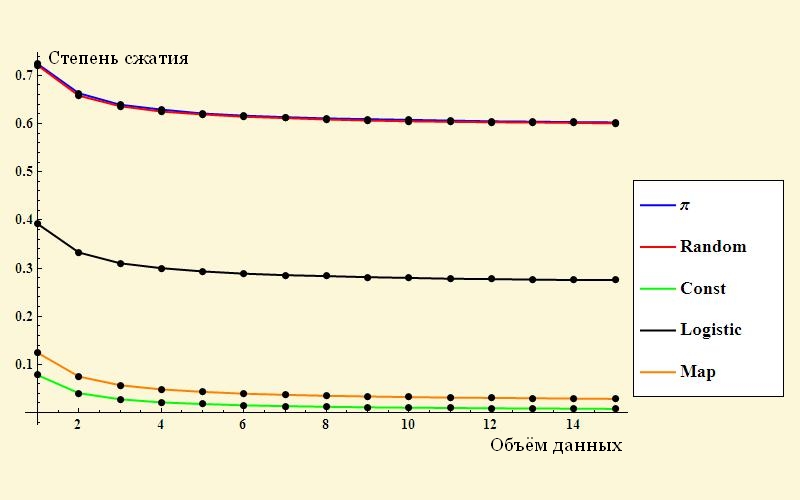
これらはすでに正しい「ビナー」写真です! 圧縮係数が制限値にどのように到達するかが明確にわかります。これは、初期データのランダム性の尺度を特徴付けるものです。
データの順序が小さいほど、エンコードが難しくなることを思い出してください。
最大の残留量は、数字Piと乱数(ほぼマージされた青と赤の桁)
グラフィック)。
アイデアの開発の例。
「退屈な」数字の代わりに、意味のある文学的なテキストを取ります。 それらの確率論的手法と圧縮手法の程度は、非常に広範なトピックです( 例えばを参照)
ここでは、アーカイバを使用した測定も意味があることを確認します。
例として、ロシアのおとぎ話のほぼ等しい文章、ジェッダクリシュナムルティの精神的な会話、L.I。のスピーチがあります。 ブレジネフ。
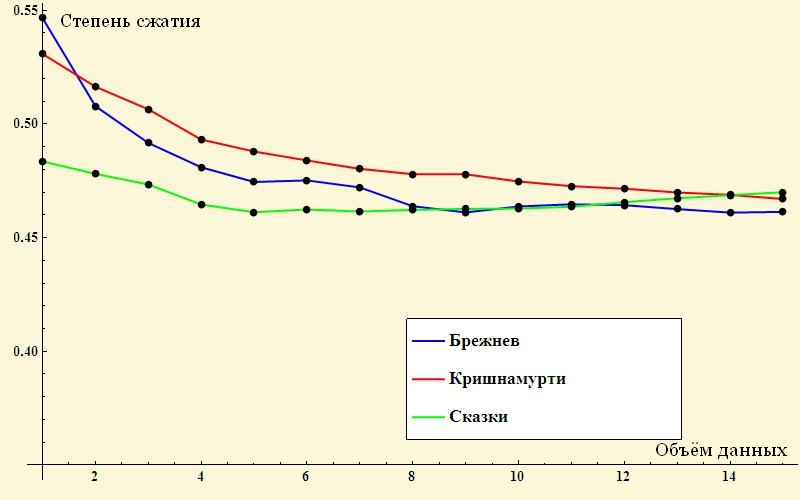
それは興味深いことが判明しました-小さなパッセージでは、テキストの圧縮(つまり、順序付け)の程度が著しく異なり、ブレジネフが先導します(!)しかし、大きな配列では、テキストのエントロピーはほぼ同じです。