👩🏻‍✈️ 🐯 🧗🏽 隠れマルコフ連鎖、ビタビアルゴリズム 👨🏿 👨🏽‍🎓 👩🏼‍⚖️

嘘発見器を実装する必要があります。嘘発見器は、人の手を震わせ、真実を伝えているかどうかを判断します。人がうそをついているとき、彼の手がもう少し揺れているとします。信号は次のようになります。

ソース信号

興味深い方法は、LR Rabinerの記事「音声認識における隠れマルコフモデルと選択されたアプリケーションのチュートリアル」で説明されています。これらのアルゴリズムは集合体にのみ関心があるという事実にもかかわらず、より良い理解のために、それらを別々に記述する方が良いです。

隠れマルコフ連鎖法は広く使用されています。たとえば、 CGアイランド（DNA、シトシンおよびグアニン結合が高密度のRNA領域）の検索に使用されますが、ローレンスラビナー自身が音声認識に使用しました。脳波による睡眠/覚醒の段階の変化を追跡し、てんかん発作を探すために、アルゴリズムは私にとって有用でした。

隠れマルコフ連鎖のモデルでは、問題のシステムには次の特性があると想定されています。

各期間で、システムは有限の状態セットのいずれかになります。
システムは誤って1つの状態から別の状態（おそらく同じ）に切り替わり、遷移の確率はそれがあった状態のみに依存します。
各瞬間に、システムは観測された特性の値を1つ与えます。これは、システムの現在の状態のみに依存するランダムな値です。

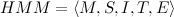
HMMモデルは次のように説明できます。 $HMM = \ langle M、S、I、T、E \ rangle$

Mは状態の数です。
$S = \ {S_1、...、S_M \}$ -条件の有限セット。
$I =（P（q_0 = S_i）= \ pi_i）$ システムが時間0で状態iにある確率のベクトルです。
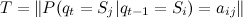$T = \ | P（q_t = S_j | q_ {t-1} = S_i）= a_ {ij} \ |$ 状態iから状態jへの遷移の確率行列 $\ forall t \ in [1、T_m]$ ;
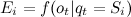、 O（すべての状態の観測可能な値のセット）で定義された密度または分布の関数として定義された各状態に対応する観測可能なランダム変数の分布のベクトルです。

時間tは、非負の整数で与えられる離散であると想定されます。0は初期の瞬間に対応し、Tmは最大値に対応します。

2つの隠れた状態があり、嘘検出器の例のように、観測値が異なる分散の正規分布に従う場合、状態ごとにシステム機能アルゴリズムは次のように表すことができます。

隠れマルコフ連鎖のスキーム

より簡単な説明は、確率モデル：例と図ですでに言及されています。

観測された量の分布のベクトルの選択は、多くの場合研究者にあります。理想的には、観測された量は潜在状態であり、この場合のこれらの状態を決定するタスクは簡単になります。実際には、すべてがより複雑です。たとえば、Rabinerによって記述された古典的なモデルは、 E_i

-有限離散分布。以下のグラフのようなもの：

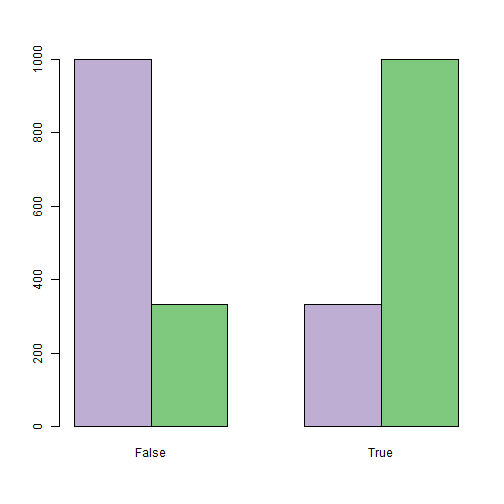
研究者は通常、観測された状態の分布を自由に選択できます。観測値が隠された状態を区別するほど、優れています。プログラミングの観点から見ると、観察可能なさまざまな特性を列挙するには、慎重にカプセル化する必要があります E_i

。下のグラフは、うそ発見器問題の初期データの例を示しています。観測された特性（手ぶれ）の分布は、両方の状態で平均0、人が真実（紫の列）と1.21横になっているとき（緑の柱）：

モデルのセットアップの問題に触れないために、単純化されたタスクを検討します。

与えられた：

公正な動作が分散が1のホワイトノイズに対応する2つの隠れた状態-分散が1.21のホワイトノイズ。

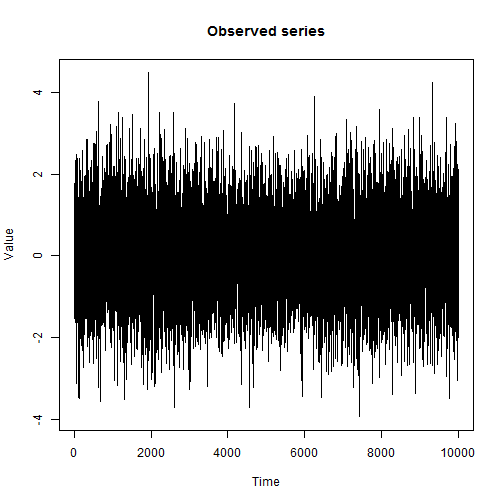
10,000連続観測のサンプルo;

状態の変化は、平均で2,500サイクルごとに発生します。

状態遷移の瞬間を判断する必要があります。

解決策：

モデルの5つのパラメーターを設定しましょう：

状態数M = 2;
S = {1,2};
経験によれば、初期分布は実質的に無関係であるため、I =（0.5,0.5）です。
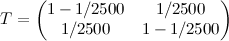$T \左矢印\左（\ begin {matrix} 1-1 / 2500および1/2500 \\ 1/2500および1-1 / 2500 \ end {matrix} \右）$ ;
E =（N（0,1）、N（0,1.21））。

与えられたモデルパラメーターに対してビタビアルゴリズムを使用して、各瞬間の最も妥当な状態を見つけます。

問題の解決策は、モデルの指定とビタビアルゴリズムの実行に限定されます。

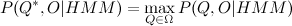隠れマルコフ連鎖のモデルと観測された特性の値のサンプルによれば、与えられたモデルのサンプルを最もよく記述する状態のシーケンスを見つけます。概念はさまざまな方法で最もよく解釈できますが、十分に確立された解決策はビタビアルゴリズムです。 $Q ^ * =（q_0、..、q_ {T_m}）、q_i \ in S$ あれ $P（Q ^ *、O | HMM）= \ max \ limits_ {Q \ in \ Omega} P（Q、O | HMM）$ 。

検索タスク Q ^ *

動的計画法を使用して解かれたため、このために関数を検討します。

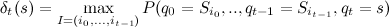
$\ delta_t（s）= \ max \ limits_ {I =（i_0、...、i_ {t-1}）} P（q_0 = S_ {i_0}、..、q_ {t-1} = S_ {i_ {t-1}}、q_t = s）$

どこで $\ delta_t（s）$ 時間tで状態sにいる最大の確率です。再帰的に、この関数は次のように定義できます。

$\ delta_0（s）= \ pi_s f_s（o_0）、\ delta_t（s）= \ max_ {s '\ in S}（\ delta_ {t-1}（s'）a_ {s's}）f_s（o_t）$

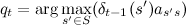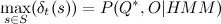計算と同時に $\ delta_t（s）$ 時間ごとに、私たちが来た最も可能性の高い状態、つまり $q_t = \ arg \ max \ limits_ {s '\ in S}（\ delta_ {t-1}（s'）a_ {s's}）$ 最大値に達したとき。同時に $q_ {T_m} = \ arg \ max \ limits_ {s \ in S}（\ delta_ {T_m}（s））$ 、そしてあなたは復元することができます $Q ^ * =（q_0 ^ *、...、q_ {T_m} ^ *）$ それらを逆の順序で歩きます。あなたはそれに気付くかもしれません $\ max \ limits_ {S \ in S}（\ delta_ {t}（s））= P（Q ^ *、O | HMM）$ 希望する確率の値です。必要なシーケンス Q ^ *

見つかりました。アルゴリズムの興味深い特性は、観測された特性の推定関数が $\ delta_t（s）$ 因子の形で。仮定すると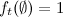

、その後、観測の省略の場合、これらの瞬間で最も可能性の高い潜在状態を評価することが依然として可能です。

ビタビのアルゴリズムの擬似コードの概要を以下に示します。ベクトルと行列を使用したすべての演算は要素ごとに行われることに注意してください。

Tm<-10000 # Max time M<-2 # Number of states S<-seq(from=1, to=M) # States [1,2] I<-rep(1./M, each=M) # Initial distribution [0.5, 0.5] T<-matrix(c(1-4./Tm, 4./Tm, 4./Tm,1-4./Tm),2) #[0.9995 0.0005; 0.0005 0.9995] P<-c(function(o){dnorm(o)}, function(o){dnorm(o,sd=1.1)}) # Vector of density functions for each state (N(0,1), N(0,1.21)) E<-function(P,s,o){P[[s]](o)} # Calculate probability of observed value o for state s. Es<-function(E,P,o) { # Same for all states probs<-c() for(s in S) { probs<-append(probs, E(P,s,o)) } return(probs) } viterbi<-function(S,I,T,P,E,O,tm) { delta<-I*Es(E,P,O[1]) # initialization for t=1 prev_states<-cbind(rep(0,length(S))) # zeros for(t in 2:Tm) { m<-matrix(rep(delta,length(S)),length(S))*T # delta(s')*T[ss'] forall s,s' md<-apply(m,2,max) # search for max delta(s) by s' for all s max_delta<-apply(m,2,which.max) prev_states<-cbind(prev_states,max_delta) delta<-md*Es(E,P,O[t]) # prepare next step delta(s) } return(list(delta=delta,ps=prev_states)) # return delta_Tm(s) and paths } restoreStates<-function(d,prev_states) { idx<-which.max(d) s<-c(idx) sz<-length(prev_states[1,]) for(i in sz:2) { idx<-prev_states[idx,i] s<-append(s,idx,after=0) } return (as.vector(s)) }

誰かがこの「擬似コード」のRコードを認識できますが、これは最良の実装にはほど遠いです。

シミュレーション中に設定された状態の不変の期間（グラフの上部）と、ビタビアルゴリズムを使用して検出された状態（グラフの下部）を比較します。

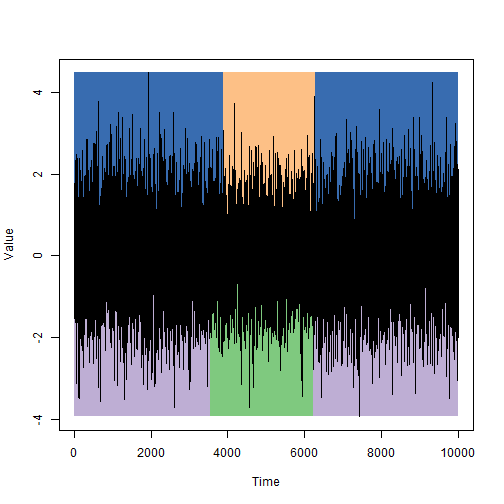
私の意見では非常に価値がありますが、そのたびに期待するべきではありません。

前述のビタビアルゴリズムでは、隠れマルコフチェーンモデル（ビタビ関数の引数）の定義が必要です。それらのタスクには、単純な初期化が使用されます。これは、Oの観測値の選択に加えて、どこかでわかっている対応する隠し状態Qの選択も与えられることを意味します。この場合、パラメーターを評価するための式は次のようになります。

$S \左矢印\左\ {s：q_t = s、t \ in [0、T_m] \右\} \\ M \左矢印\ | S \ | \\ I \左矢印\左（\ frac {\ sum_ {t \ in [0、T_m]} Id（q_t = s）} {T_m + 1}、s \ in S \右）\\ T \左矢印\左（\ frac {\ sum_ {t \ in [1、T_m]} Id（q_ {t-1} = s '、q_t = s）} {\ sum_ {t \ in [0、T_m]}（\ sum_ { t \ in [1、T_m]} Id（q_ {t-1} = s '）}、s、s' \ in S \ right）\\ E \ leftarrow \ left（f_s（o_t）= \ frac {\ sum_ {t \ in [0、T_m]} Id（q_t = s、o_t = e）} {\ sum_ {t \ in [0、T_m]} Id（q_t = s）}、s \ in S \右）$

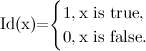
Id（x）はインジケーター関数です。 $Id（x）= \ begin {cases} 1、\ mbox {xはtrue}、\\ 0、\ mbox {xはfalse。} \ End {cases}$

対象の嘘発見器の例では、アルゴリズムは10,000の状態から413（〜4％）を誤って分類しましたが、これはまったく悪いことではありません。ビタビアルゴリズムは、観測された特性の分布が正確にわかっている場合にのみ、潜在状態の変化の瞬間を高い精度で検出できます。そのような分布のパラメトリッククラスのみがわかっている場合は、Baum-Welshアルゴリズムと呼ばれる最適なパラメーターを選択する方法があります。

興味がある場合は、もっと尋ねてください...

隠れマルコフ連鎖、ビタビアルゴリズム

More articles: