第二部の第一部
第二部の第二部
さて、紳士、それは終了する時間です。 サイクルの最後の記事(タイトルがまだ目覚めているテンプレートを破る)で、このタスクの履歴に弾丸を付けます。 第二部へのコメントではこれを行うためのより便利で普遍的な方法が提案されたという事実にもかかわらず、私はまだ記事の最初を書く前に私が個人的に開発したツールを使用します。 第一に、良さが失われることはありません。第二に、GeoGebraで美しい絵を描いてハブに投稿するだけの口実であることを誰もが理解していると思います。 まあ、彼らが言うように、それは始まりました。
ケース3:対称性の移動
スライド対称性は、対称軸とそれに平行なせん断ベクトルのパラメーターによって決定されます。 対称軸は、平面上の方向と特定の位置によって決まります。 次に、相互に続く多くの事実の概要を説明します。これらの事実は、それらを補題とさえ呼べないほど明白であり、証明するほどではありません。
- 移動対称の軸は境界から等距離にあります(並列転送の場合から境界の概念を非選択的に取得します)。
- 異なる境界に端を持つセグメントを取る場合、対称軸はその中央を通過します。
- 移動対称軸の方向を設定すると、その特定の位置が自動的に認識されます。 両方の境界が単一のポイントで構成されている場合、シフトベクトルもわかります。
- 図が軸で分割される部分の面積は等しくなります(この事実は前のものからは続きません)
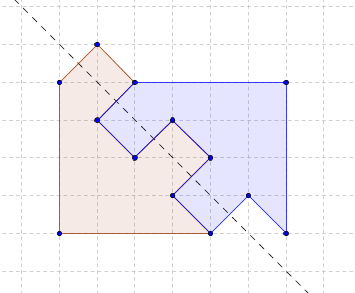
これらの事実を武器に、私はこの絵を描きました。

境界線のほとんどの方向では、ポイントAとE、またはポイントBとFのいずれかが存在するため、軸は図の「中心」(長方形ABEFの対角線の交点)を通過することがわかります。 有病率の2番目の場所は、ポイントCとFのケース、名誉ある3番目のポイント-ポイントCとAのケースで占められています。これらのケースでは、明らかに、対称軸はセグメントCFとCAの中間点を通過します。
ここで、軸が図を2つの等しい部分に分割する方向を見てみましょう。 面倒な詳細に進むことなく、私は簡単に言います:しかし、そうです。
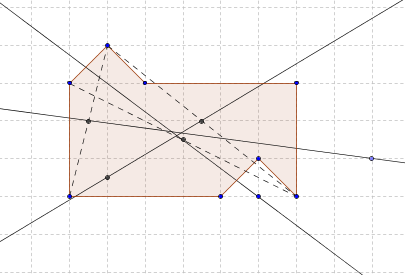
3つの特定の軸があり、さらに3つの特定のシフトベクトルがそれらにアタッチされています-すべての場合の境界は1つのポイントで構成されているためです。 これらの3つの移動対称すべてに、画像または逆画像がない図形のポイントがあることを示すのは簡単です-補題3によれば、これらは、図形を2つの等しい部分に分割することに対応できない悪い、価値のない移動対称であることを意味します。 特定のポイントの検索は読者に任せます。
おわりに
図A 0を2つの等しい部分にカットすることはできません 。 今、私は「ここの夜明けは静かだ」と修正するために明確な良心をもって行きます。 幸せな勝利の日、ハブロビテス同志。