はじめに

最近、Haskell のリストに関する記事を読んだので、FNP（F＃）の基本構造の実装についても少し話すことにしました。インターネットには既製の実装が数多くあるため、この記事には実用的な価値はありません。この記事の目的は、F＃に不変キューを実装する方法と、その動作について説明することです。

まず、いくつかの用語。

F＃は.NETファミリのプログラミング言語であり、オブジェクト指向の命令型アプローチに加えて、プログラミングへの機能的アプローチを実装しています。

不変オブジェクトとは、一度作成されたときに将来変更できないオブジェクトです。たとえば、C＃には文字列などのデータ型があり、そのインスタンスは不変です。文字列に文字を追加すると、新しい文字列が取得され、古い文字列は変更されません。詳細はこちら。

単一リンクリスト

キューを実装するには、単一リンクリストが必要です。単リンクリストはそのようなデータ構造であり、各要素には保存された値と前の要素へのリンクが含まれていることを思い出してください。

F＃で同じこと：

type public 'a List = //  List  generic- 'a,     | Empty //  | Node of 'a * 'a List //:  -   ("")

このエントリは、リストが空であること、または「head」と「tail」のペアのいずれかであることを意味します。「tail」もリストです。

リストの基本操作を検討し、複雑さを評価してください。

リストにアイテムを追加

要素を追加すると同時に古いリストを変更せずに残すには、新しいリストを作成する必要があります。ここで、headは追加する要素、tailは古いリストです。 F＃では、1行で記述されます。

 member this.Cons x = Node(x, this)

その後、元のリストと新しいリストの2つのリストが既にあります。同時に、両方のリストは、1つの最終リストが占有するのと同じ量のメモリを占有します（下図を参照）。

図では、List1はアイテムを追加する前のリスト、List2はアイテムを追加した後のリストです。 さらに、List1はList2の末尾でもあります。

明らかに、アイテムを追加する複雑さはリストの長さに依存せず、O（1）に等しくなります。

リストからアイテムを抽出する

アイテムの取得は追加するのと同じくらい簡単です。最後に追加された要素は、単に「ヘッド」から取得されます。この要素のないリストを取得するには、「テール」を使用します。

 member this.Head = match this with | Empty -> failwith "Empty stack" | Node(head, tail) -> head member this.Tail = match this with | Empty -> failwith "Empty stack" | Node(head, tail) -> tail

明らかに、これらの操作の複雑さはO（1）です。

リストスプレッド

リストに対するもう1つの便利な操作はスプレッドです。アイテムの並べ替え。元に戻すには、元のリストから要素を順番に抽出し、新しいリストに配置する必要があります。新しいリストと古いリストには共通のデータはありません。複雑さは常にO（N）です。以下のコードと図：

 let rec reverse destList sourceList = match sourceList with | Empty -> destList | Node(sourceHead, sourceTail) -> reverse (Node(sourceHead, destList)) sourceTail

図では、List1は反転前のリスト、List2は反転後のリストです。

キュー

スタックの実装には、追加および取得操作を含む単一リンクリストが理想的です。ただし、このようなリストをいくつか取得する場合は、キューを実装できます。

キューは、要素へのアクセスの原則が「先着順」（FIFO）のデータ構造です。

キューを実装するには、新しい要素が追加される後部リストと、要素が抽出される前部リストが必要です。

 type 'a Queue (front:'a List, rear: 'a List) = //   Queue    static member Empty = Queue(List.Empty, List.Empty) //   -

キューへのアイテムの追加

キューにアイテムを追加すると、バックリストにアイテムが追加されます。つまり、フロントリストが同じで、新しいアイテムを追加してバックリストを取得する新しいキューを作成します。

  member this.Snoc value = Queue(front, rear.Cons value)

明らかに、アイテムをキューに追加する難しさの評価は、単純に接続されたリストにアイテムを追加する難しさの評価と一致します-O（1）。

キューからアイテムを取得する

正面リストからアイテムを抽出する前に、空かどうかを確認します。空の場合は、背面を開いて展開します。前面になり、空のリストを背面に割り当てます。最悪の場合の複雑度は、O（N）リストロールの複雑度と同じです。

  let frontToBack = match front, rear with |Empty, rear -> (rear.Reverse, Empty) |x -> (x) member this.Head = match frontToBack with | Empty, _ -> failwith "Empty or not reversed" | List.Node(a, __), _ -> a member this.Tail = match frontToBack with |Empty, _ -> failwith "Empty" |List.Node(a, tail), r -> Queue(tail, r)

以下は、キューの「寿命」の図であり、追加および抽出の操作の順次実行を示しています。

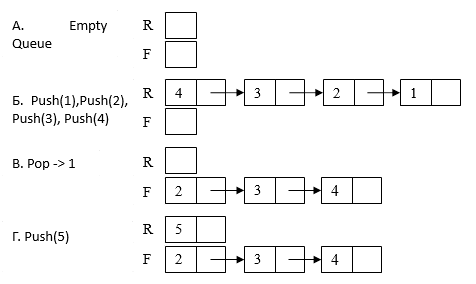
図には4本の線が模式的に示されています：A-空のキュー、B-番号1、2、3、4を連続して追加した後のキューC-1つの要素（番号1）を抽出した後のキュー、G-番号5を追加した後のキュー

おわりに

記事の冒頭で検討した単一リンクリストは、スタックとしてだけでなく、ランダムアクセスのコレクションとしても使用できます。これを行うには、挿入および削除操作が必要です。それらの複雑さは挿入/削除の場所に依存し、最悪の場合O（N）に等しくなります。実装は読者に任せます。

一部の操作のリストとキューの両方は、最適な複雑さではありません-O（N）。実装で遅延計算が正しく適用されると、状況はO（1）まで改善されます。これがどのように行われるかについては、尊敬される読者がトピックに関心を示しているかどうかを次の記事で説明します。

中古文学

Chris Okasakiの著書「Purely Functional Data Structures」は、主な情報源として使用されました。

F＃の不変キュー