フラットチャネル内の流れの安定性の問題の例については、テキストでもう少し理論を書きます。 実際には、このような問題は非常に多くあります。層やさまざまな形状の限られた空洞、垂直層、水平層、傾斜層、通常の液体や多孔質媒体、磁場の影響下にある導電性流体、温度の影響下にある塩の溶液、任意の方向の振動の影響下にある、2つの液体間の界面にある空洞...一般に、流体力学のすべてのサブレベルの単なるリストには数時間かかる場合があり、すべてを覚えていることはほとんどありません。 また、追加の要因（約700 kBの画像）の影響なしに、流れの純粋な流体力学的不安定性のいくつかの例を示します。
以前の投稿は、後続の投稿で数式の数学的および意味的な基盤を提供するために書かれました。
流体力学について簡単に説明すると、どのようにしてすべてが始まったのか覚えていますか？
流体力学について簡単に：運動方程式
流体力学について簡単に：エネルギー保存
一般に、安定性の理論は非常に広い分野であり、理論力学と線形および非線形振動の理論（最も開発されている場所）の両方で見つけることができます。 具体的には、研究対象の詳細と対応する方程式系により、流体力学的安定性の理論を保持しています。 いくつかの最も単純な（そして最も基本的な）例について考えてみましょう。
二次元の流れの安定性
非圧縮性の粘性流体の任意の流れを考えてみましょう。 当然、Navier-Stokesの方程式で記述されます。
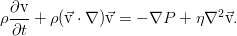
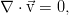
方程式はまだ次元形式です。 しかし、それらはさらなる作業のために都合よく測定されません。 この操作により、パラメーターの数が減り、システムの動作で最も重要なメカニズムをすぐに確認できます。 無次元化の手順は、パラメーターの数を最小限に抑えるような方法ですべての変数を再スケーリングすることで削減されます。 ほとんどの場合、時間スケールは決定することになります-特徴的な時間をその単位として選択できます。その間、特徴的な速度のフローがチャンネルの特徴的な長さを通過します（簡潔にするために、学校関係時間=距離/速度ですが、そのような用語はどこにも見当たりません）、パルスの伝達時間（粘性時間）、熱（熱時間）、外部の影響など チャネル内の運動方程式については、運動時間をとり、速度、長さの任意のスケールを示し、方程式の最大の単純化に基づいて圧力のスケールを選択するのが最も便利です。
方程式のスケールを置き換えて、非線形項の前の密度と係数で縮小すると、粘性項を除き、すべての係数が1に等しくなることがわかります。 そこでは、パラメーターの組み合わせが逆レイノルズ数を表します。
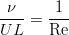
この種の2番目の方程式は、無次元の場合は変わりません。 したがって、レイノルズ数は、システムの動作を決定する唯一のパラメーターです。
シックなのは、この1つのパラメーターのみが流れの層流または乱流の原因であり、方程式は少し変化しないことです。
さらに、ある速度で一定の時不変の流れがあるとします
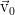、およびこのフローにはわずかな摂動があります：
この形式でシステムに速度と圧力を安全に代入し、速度と圧力の定常場のみを含むすべてのものをドロップできます。 それらはそれ自身で方程式を満たし、非線形項を無視することは理論全体で最も重要な動きです。 なぜなら 摂動は無限小であると見なし、次の形式の項
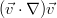2次の無限小になります。 したがって、外乱がまだ小さいと考えられる分野で作業している（つまり、将来の不安定性の発生の非常に最初の段階で）と言って、非線形性を安全に破棄できます。 その結果、変数係数はありますが、2つの線形方程式が残ります。
このシステムは、流体力学的安定性の線形理論の方程式の基本的なシステムであり、最も一般的な状況を説明しています。 次に、もう1つの特定の状況を見てみましょう。特定のチャネルでの平面平行流の安定性です。 すべてが（ x 、 z ）平面で発生し、 y軸に沿ってチャネルは無限に拡張されます-つまり、純粋に2次元の流れです。 定常解には、チャネルの横座標に依存する1つのコンポーネントのみがあり、外乱には2つのコンポーネントがあるとします。
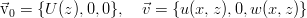
また、指数の時間依存性も受け入れます（方程式は線形であり、指数はそれらの典型的な解であるため）
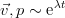。 このような障害は通常「正常」と呼ばれますが、この用語の歴史はかなりあいまいです。 示された依存関係を代入し、軸上の投影の方程式を書き留めて、平面摂動のシステムを取得します。 さらに、その中の係数はx座標に依存しないため、摂動はこの軸に沿って周期的であるとさらに仮定することができます-実際、これはフーリエ級数に拡張し、1つの成分のみを考慮しています： 
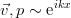。 すでに常微分方程式からそのようなシステムが判明しています（素数はzに関する微分を示します）：
単純ですが数ページかかる中間変換を省略すると、このシステムは速度成分wの単一の方程式に還元できることがわかります。
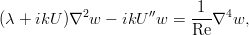
複素増分を書き込み、外乱の位相速度を導入すると
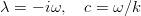
Orr-Sommerfeld方程式として知られる方程式が得られます。
流れの流体力学的安定性の線形理論全体は、この方程式に基づいています。 確かに、定常流のタイプや境界条件に関係なく、正確な解決策はありませんが、外見的にはすべてが非常に単純に見え、タスクは閉じられます。
この問題を解決するためのさまざまなアプローチがありました。 例えば、大きなレイノルズ数の近似におけるレイリーは、単に右辺を無視しました。 もちろん、4次導関数は分母を簡単に補正できるため、これは常に正しいとは限りません。 確かに、方程式を解くことはまだ不可能でしたが、流れの安定性に必要な条件に関する定理を証明することが判明しました。 確かに、この条件はポアズイユの流れでは満たされていませんが、それでも不安定になる可能性があります。
同じ近似で、小さなパラメーターとしてレイノルズの逆数を拡張することができます。 この展開のゼロ次で、前述のレイリー問題を取得します。さらに進むと、パラメーター平面（ k 、Re）で2つの曲線をキャッチできます。その間に、摂動が増加し、定常プロファイルの破壊につながる流れの不安定領域が見つかります
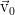。 最初、ハイゼンベルグ（行列量子力学の作成者である同じウェルナーハイゼンベルグ）は、ポアズイユの流れについてこの問題を解決しようとしましたが、分解を完全には完了できませんでした。 その結果、1944年、中国人の患者であるLin Jia-Jiaoはビジネスに取りかかり、分解をさらに拡張し、両方の曲線を外挿し、1つに閉じました。 彼は次のことを知っていました（実線）：
実際、このグラフはすでに別のシステムのビットです-通常の流体の代わりに、著者はチャネル内のいくつかの繊維の懸濁液を検討しましたが、その意味は同じであり、Linの理論との有意な質的な違いはありません（You Zhenjianga、Lin Jianzhonga、Yu Zhaoshengbからの図流路内の繊維懸濁液の流体力学的不安定性 。Fluid Dynamics Research、Volume 34（4）、2004、pp。251–271）。 一般に、ほとんどすべての流体のポアズイユ流には、Linの結果の基本的な性質を強調するだけの安定性があります。
不安定性の例
以下は、「流体とガスの流れのアルバム」（M.ヴァンダイク）とネットワークからのほとんどが引き裂かれた写真で、特定の問題の記述に関する小さなコメントがあります。
ポアズイユ流の不安定性の発達
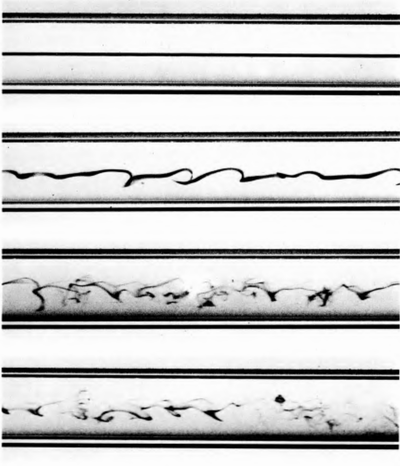
この実験は1883年にレイノルズによって行われました。写真は同じ施設で撮影され、約100年後に安全に保存されました。 写真の上から下に向かって、流量が増加します。 薄い色のトリクルがストリームに導入され、フローの優れた視覚化が可能になります。
流体柱の不安定性（レイリープラトー問題）
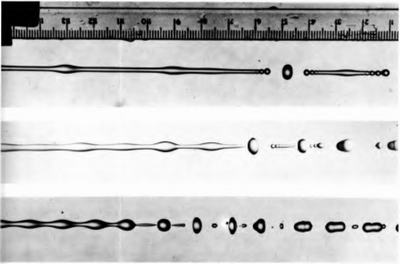
毎日観察できる非常にエレガントな不安定性。 蛇口を開いて、細流が均一で薄くなるようにしますが、同時に十分な長さです。 ランダムな摂動と毛細管力の相互作用により、連続的な流れは小さな液滴に分割される傾向があります。 それはエネルギー的により有益です。 ここでは、出力チューブが接続されているスピーカーのために液体がinしています。 下の図の摂動波長は、理論上の臨界値に近いです。
レイリー・テイラー不安定性
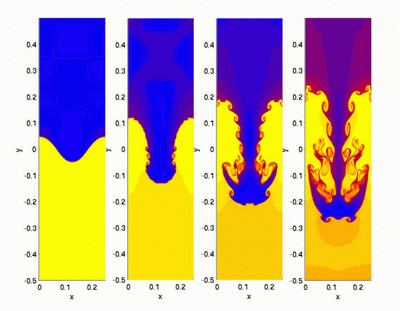
かなり簡単な状況-軽い液体の表面に重いものを注ぎます。 重いものは「転倒」する傾向があることは明らかですが、当面は表面張力がプロセスに耐えることができます。 しかし、動きが始まると、実験室と計算の両方で、そして自然の中で非常に美しく起こります（著者、写真家の考えによれば、2番目の写真は逆さまです）。
媒体内に非常に異なる圧力を持つ2つの領域が存在する場合、同様の現象が観察されます。それらの界面を介して、物質は「絞り」、単純な「ディップ」に類似した構造を生じます。
テイラー・ワールウィンズ
不安定性の別のバージョン、似たようなテイラーレイリーの起源。 流体は2つの同軸シリンダーの間にあり、高速回転で駆動されます。 求心性の加速により、反対方向の流れ方向を持つ環状セルが媒体内に形成され、最初はシリンダー壁に対して静止しています。
ケルビン・ヘルムホルツ不安定性
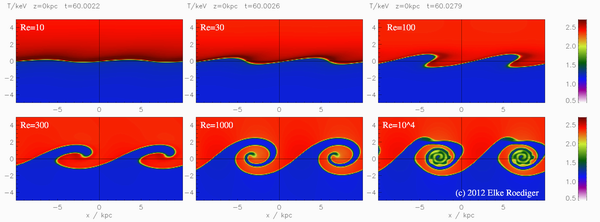
不安定性の別のバージョン。 また、物理的に、非常に簡単です。 互いに反対方向に移動する不混和性液体の2つの流れがあります。 または単に異なる速度で-つまり それらの間の界面では、表面の摂動が変形、ねじれ、複雑な渦を発生させる速度ジャンプがあり、液体を完全に混合します。 計算、実験のセットアップ、および自然の面でも同じように興味深いものです。
ここでは、もちろん、起こりうる不安定性の全スペクトルからはほど遠い-この領域は無尽蔵であり、これまで未踏の現象とその特徴の膨大なスペクトルが含まれています。 次の投稿は、システム内の温度の不均一性によって引き起こされる対流と対応する不安定性についてです。