こんにちは この投稿では、 限られたボルツマンマシンで実験を続けます。 BSRの正則化に関する以前の投稿で、より一般化する能力を備えたより多くのローカル機能を取得する方法を説明しました。 しかし、単純で高速なアルゴリズムと比較した場合の堅牢性は評価しませんでした。 この実験では、 主成分の線形法を使用します （この方法に慣れて、 最初の投稿でc＃の実装を見てください）。 BSRを使用した次元圧縮の理論に関する主要な情報源に慣れたい場合は、Jeffrey Hinton の記事をこことここで参照することをお勧めします 。 多くの印刷された大文字のテストを続けます：BSRをトレーニングし、主要なコンポーネントを構築し、データの圧縮表現を生成し、そこから元の画像を復元し、元の画像と復元された画像の違いを評価します。
線形主成分
あなたが主成分の方法に精通していることが理解されている、そうでなければ、 あなたはここにいる 。 この実験では、29 x 29ピクセルの画像を多数使用します。これは、4つの異なるフォントと3つのスタイルの英語のアルファベットの大きな文字と、ノイズのある同じ画像、合計4056画像を示します。 テストセットは同じ文字のセットで構成されていますが、ノイズが多い-3432個です。 それでは、R言語では、コードは非常にシンプルに見えます：
m.pca <- eigen(cov(m))
。 主要なコンポーネントの重要性は、その主要な値によって推定できます。まず、これらの値の合計で正規化します。 その結果、次のグラフが得られます。 最初は各主要コンポーネントが説明する変動の割合を示し、2番目は各ステップで説明された変動の合計を示します。
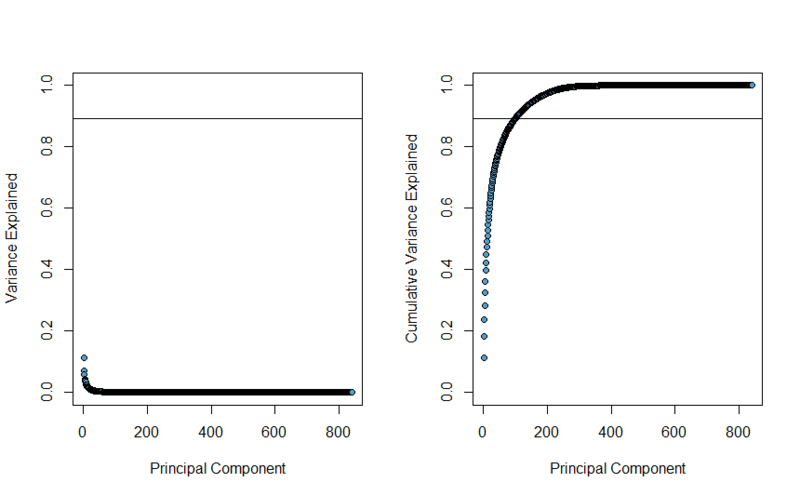
BSRでは、100個の非表示状態を使用するため、正直に言うと、変動の89.36％を説明する最初の100個の主要コンポーネントを選択します。このレベルは上のグラフの線で示されます。
各主要コンポーネントは、データセットの一部の特徴を検出する29 x 29ピクセルの画像として解釈できます。 限られたボルツマンマシンの隠れたニューロンの重みとの類似性を引き出し、 以前の 投稿で行ったのと同じ方法で視覚化できます。 2番目の画像では、黒はゼロ値に対応し、赤成分の増加は正の方向、青の値-負の値の増加をそれぞれ意味します。
主要コンポーネントの順序は、左から右、上から下です。 機能は非常に大きいことが判明し、各機能はトレーニングセットの文字サイズとほぼ同じサイズになっています。 最初のいくつかのコンポーネントを除き、スピーチはまったく解釈の対象にはなりません。
制限付きボルツマンマシン
この実験では、 前の投稿で説明したL1正則化の設定を使用しましたが、変更されたのは（上記の）トレーニングセットのみで、反復回数は5000で、約14時間かかりました（今すぐGPUに転送する必要があります）。 この時点で、相互検証エラーはまだ低下していたため、トレーニングを続行できます。 その結果、以下の重みが得られました。
ご覧のとおり、特徴は非常に局所的であり、基本的にこれらは小さな斑点や境界線などのプリミティブです。それらのいくつかを組み合わせることで、トレーニングセットの画像のトポロジの特徴を調べることができます。 それらの局所性のため、ニューロンの非常に小さな受容体フィールド、すなわち 各ニューロンの重みの0〜95％。これにより、データ投影アルゴリズムの速度が大幅に向上します。これは非常に重要です。
ヒーリング能力
2つのモデルを使用して復元された画像の例を見てみましょう。 最初の列には元の画像が、2番目にはPCAによって復元され、3番目にはRBMによって復元されます。
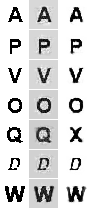
PCA再構成の背景がグレーすぎることを確認したとき、私はeigenfaceとの類推により、平均値で正規化しようとしましたが、最終的に、復元された画像は上記とほとんど変わりませんでした。 拡大された例では、境界に沿って画像がぼやけていることが示されていますが、PCAの場合はわずかに大きくなっています。
画像間の距離の推定として、 L1メトリックを使用します 。
結果は次のとおりでした。テストセットがBSRモデルの構築にも主要コンポーネントの計算にも関与しなかったことを思い出します。
| PCA | RBM | |
|---|---|---|
| 列車セット | 29.134736802449488 | 21.79797897303671 |
| テストセット | 49.231927648058118 | 29.970740205433025 |
RBM側の両方のケースで結果を見ることができます。
おわりに
BSRには、品質を改善するいくつかの方法があります。 まず、5000回の反復で学習を停止しましたが、クロス検証エラーが増大し始めるまで学習を続けることは可能ですが。 第二に、学習オプションを引き続き使用できます。 第三に、機能は非常に局所的であり、アルゴリズムの速度を上げることができます。 第4に、BSRの多くの機能がほぼ同一であることに気付くのは簡単です。これにより、機能をクラスター化し、クラスターを結合して、値を複数回計算したり、より少ない隠れニューロンでBSRをトレーニングしたりする機会が与えられます。