大学で勉強している間、私たちに教えられた統計コース(これは15年以上前でした)は最も典型的なものでした:確率論と頻繁な分布による紹介です。 それ以来、この学期のコースについて、私の頭にはこれ以上何も残っていません。 統計物理学の過程で多くの方がずっと良く与えられているように思えます。 ずっと後に、生命は医学物理学に直面しました。統計物理学は、たとえばNMRトモグラフィーを使用して得られたデータを分析するための主要なツールの1つです。 堅牢な統計と堅牢な推定量という用語に出会ったのはこれが初めてです。 すぐに予約します。堅牢な推定器の使用の簡単な例のみを示し、文献へのリンクを示します。興味のある人は、この記事の最後にある文献リストを使用して知識を簡単に深め、広げることができます。 サンプルで信頼できる推定値を示すために、最も頻繁に遭遇する最も単純な例を見てみましょう。 学生のVasyaが物理的なワークショップに座って、特定のデバイスの証言を書き留めるとします。
4.5
4.1
5.2
5.5
3.9
4.3
5.7
6.0
45
47
デバイスは非常に正確に動作しません。さらに、Vasyaはレナの開業医との会話に気を取られます。 その結果、Vasilyは最後の2つのエントリに小数点を入れません。そして問題があります。
ステップ1、サンプルを昇順でソートし、平均値を計算します
平均= 13.12
サンプルに落ちた最後の2つの外れ値により、平均値が実際の平均からかけ離れていることがすぐにわかります。 排出の影響を考慮に入れずに平均を推定する最も簡単な方法は、中央値です
中央値= 5.35
したがって、最も単純なロバストな推定量は中央値です;実際、データの最大50%がさまざまな種類の外れ値で「汚染」されることがわかりますが、中央値の推定値は変化しません。 この簡単な例を使用して、いくつかの概念を一度に導入できます:統計の堅牢性(データの外れ値に関する推定の安定性)、使用された推定器の堅牢性(取得した推定値を大幅に変更せずにデータを「汚染」できる程度)[1]。 中央値スコアを改善できますか? もちろん、中央値からの絶対偏差(中央絶対偏差またはMAD)として知られる、より信頼性の高い推定量を入力できます。
MAD =中央値(| xi-median [xj] |)
正規分布の場合、数値因子がMADの前に導入されるため、推定値を変更せずに維持できます。 ご覧のとおり、MADの安定性も50%です。
堅牢な推定器は、線形回帰に非常に実用的であることがわかりました。 線形依存性(x、y)の場合、そのような依存性の適切に調整された推定値を取得する必要がしばしばあります(多変量回帰の場合)
y = Bx + E 、
ここで、 Bはすでに係数の行列である可能性があり、 Eは測定値を損なうノイズであり、 xは y (ベクトル)の測定値を使用して実際に評価したいパラメーター(ベクトル)のセットです。 これを行う最も簡単で最もよく知られている方法は、最小二乗法(最小二乗法)です[2]。 原則として、最小二乗法がロバストな推定量ではなく、ロバストな信頼性が0%であることを確認するのは非常に簡単です。 単一の外れ値でさえ、推定値を大きく変える可能性があります。 スコアを改善するための最も数学的な美しいトリックの1つは、最小トリミング正方形または「トリミング」正方形(MUK)の方法と呼ばれます。 彼のアイデアは、使用される推定値の数が削減される、元のOLSを簡単に変更することです。
元のOLS
min \sum_{i=1}^N r_i^2,
ムック
min \sum_{i=1}^h {r_i^2}_{1:N},
ここで、 r_iはすでに推定誤差(y-O(x))の順序付けられたエラーです。 r_1 <r_2 <... <r_N 。 繰り返しますが、 h = N / 2 + p ( pは独立変数に1を加えた数)の信頼できる推定を可能にする最小トリミングファクターを簡単に検証できます。 堅牢な評価の信頼性もほぼ50%になります。 実際、 hの選択に関連する1つの重要な質問を除いて、すべてはMUKで非常に簡単です。 選択の最初の目撃方法は、「視界による」として特徴付けることができます。 回帰を行うサンプルがあまり大きくない場合、特に推定値が増減しても変化しない場合は、異常値の数を推定し、いくつかの近い値を試してトリミング係数を選択できます。 ただし、より厳しい選択基準[3,4]があり、残念ながら、線形回帰の場合でも計算時間が著しく増加します。
文献でよく使用される他のよく知られている推定量を簡単にリストしてください[1]:
1)最小中央値二乗(中央値二乗法)
min median r_i^2
2)M-、R-、S-、Q-推定量、何らかの評価関数に基づく推定量(たとえば、OLSはM推定量とも呼ばれます)
誤差推定のさまざまなバリエーション(超平面を切断する瞬間など)。
3)非線形回帰の推定量[5]
便宜上、性質がまったく異なる多くの推定量が収集されるため、このリストのポイント2はやや不正確です。
ロバスト推定の単純だが非常に興味深いアプリケーションとして、NMRトモグラフィーの拡散テンソルのロバスト推定を示します[6]。 NMRトモグラフィーの興味深い用途の1つは、脳内のブラウン運動の影響を受ける水分子の拡散測定です。 ただし、さまざまな制限(神経線維に沿った動き、樹状突起内、細胞の内側と外側など)により、拡散パラメーターが異なります。 6つの異なる方向で測定を行う(拡散テンソルは正定です。つまり、その要素のうち6つだけを知る必要があります)、よく知られている信号減衰モデルを使用して、テンソル自体を復元できます。 空間方向は、パルスシーケンスの勾配コイルによってエンコードされます。 楕円体のような拡散テンソルを想像して、脳内の神経糸の画像を取得できます(たとえば、wikiの拡散MRIを参照してください)
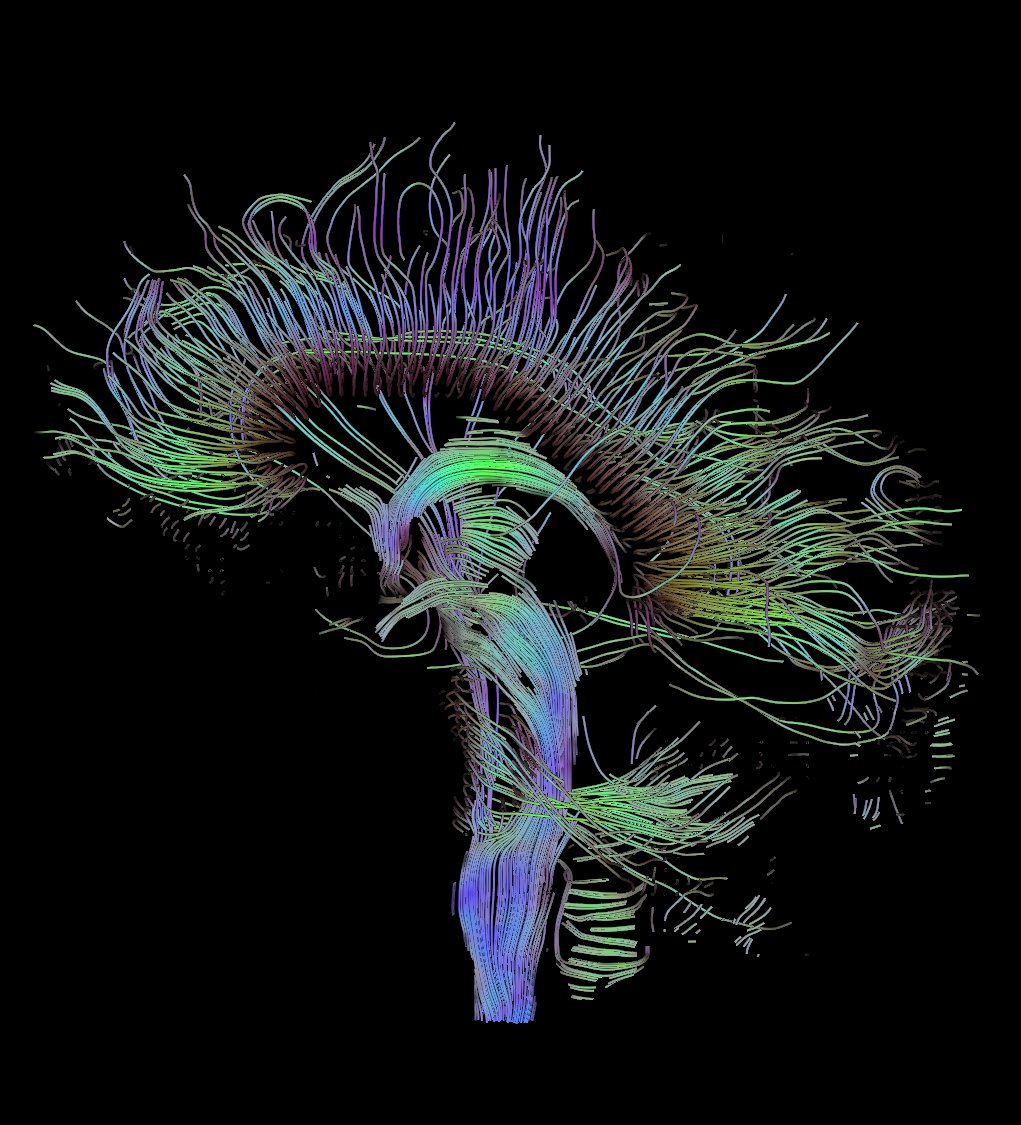
) フィラメントは、特定の曲線で近似された順序付けられたテンソルです(よく知られているルンゲクッタ法による)。 このアプローチは、合理化と呼ばれます[7]。
ただし、この種の測定は、心拍、胸の呼吸運動、測定中の頭の動き、異なるチック、頻繁に変化する磁気勾配などによるテーブルの震えなどに起因するさまざまな種類のアーティファクトで最も豊富です(他の種類の画像と比較)。 。 したがって、再構成された拡散テンソルは、実際の値から顕著な偏差を持ち、その結果、異方性が顕著である場合に間違った方向を持つ可能性があります。 これは、得られた神経線維トラックを、神経接続のデバイスに関する信頼できる情報源として使用したり、外科手術を計画したりすることを許可しません。 実際、拡散テンソル法は神経線維の画像を復元するために使用されていないため、ほとんどの患者はこれまで心配する必要はありません。
ロバスト推定量の数学的理論は非常に興味深いものです。 多くの場合、これは既知のアプローチに基づいています(これは、厳密で乾燥した理論のほとんどが既に知られていることを意味します)が、推定結果を大幅に補完および改善できる追加の特性があります。 すでに述べたOLSに戻ると、重み係数の導入により、線形回帰の場合に堅牢な推定値を取得できます。 次のステップは、推定値に反復を導入することにより重み係数を変更することです。その結果、よく知られた反復的に再重み付けされた最小二乗アプローチを取得します[2]。
堅牢な統計に不慣れな読者が堅牢な推定量についてある程度のアイデアを得て、知り合いが彼らの知識の興味深い応用を見たことを願っています。
文学
1. Rousseeuw PJ、Leroy AM、ロバスト回帰および外れ値検出。 ワイリー、2003。
2. Bjoerck A、最小二乗問題の数値解法。 SIAM、1996年。
3. Agullo、J.最小トリミング二乗回帰推定量を計算するための新しいアルゴリズム。 計算統計およびデータ分析36(2001)425-439。
4. Hofmann M、Gatu C、Kontoghiorghes EJ。 カバレッジ値の範囲のための正確な最小トリミング平方アルゴリズム。 Journal ofコンピューター統計統計19(2010)191-204。
5. Motulsky HJ、ブラウンRE。 非線形回帰でデータを近似する際の外れ値の検出-堅牢な非線形回帰と誤検出率に基づく新しい方法。 BMC Bioinfromatics 7(2006)123。
6. LC、Jones DK、Pierpaoli Cを変更します。RESTORE:oulier拒否によるテンソルのロバスト推定。 医学における磁気共鳴53(2005)1088-1085。
7.ジョーンズDK、拡散MRI:理論、方法、およびアプリケーション。 オックスフォード大学出版局、2010年。