この投稿は、微妙な状況から抜け出すのに役立ちます。 部屋に閉じ込められていて、糸と針があり、これらのオブジェクトのみを使用してPi数のおおよその値を計算するように促されているとしましょう。 それで、今日、 ペンシルベニア大学のマタンのコースをカーソルで聞いて、私は突然これを行う方法を見つけました。 Pi番号がここに隠れているため、それは推測できませんでした。 この問題のルーツは、 ジョルジュ=ルイ・ルクレール・ド・ビュフォンが次のタスクを設定した18世紀にさかのぼることが判明しました。 投げられた針が落ちて、2つのストリップを結ぶ線を横切る可能性はどのくらいでしょうか？」
シミュレーション
陰謀を損なわないために、実験から始めましょう。 したがって、長さLの多くの針と緑色の糸のかせがあります。 互いに距離Lで同じ長さの多数の平行なセグメントを表面に適用します。
このフィールドに100本の針を投げます。
おそらく十分ではありません。 900を追加し、糸を横切る針を赤でマークします。
すべての針を一度に投げるのではなく、一度に1つずつ投げ、各ステップで、糸に落ちた針の数と投げられた針の総数の比率を記録し、それによって針が落ちて糸を越える確率のより大きな近似を得ると仮定します。
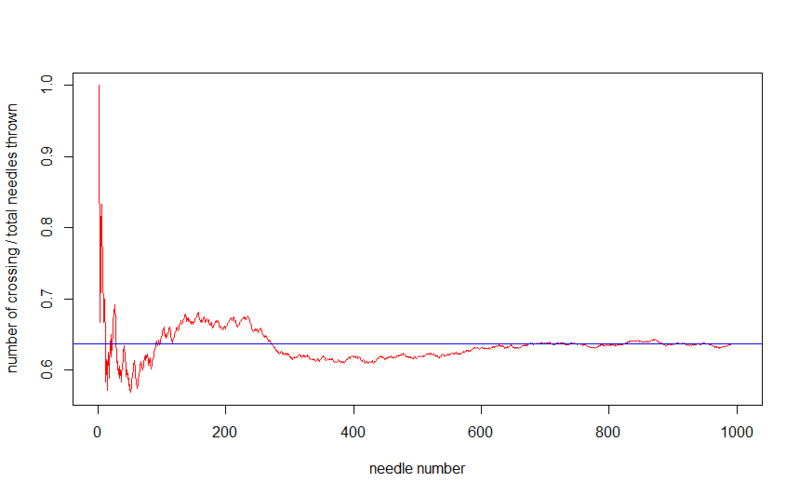
10,000本の針を落とすと、画像はより正確になります。
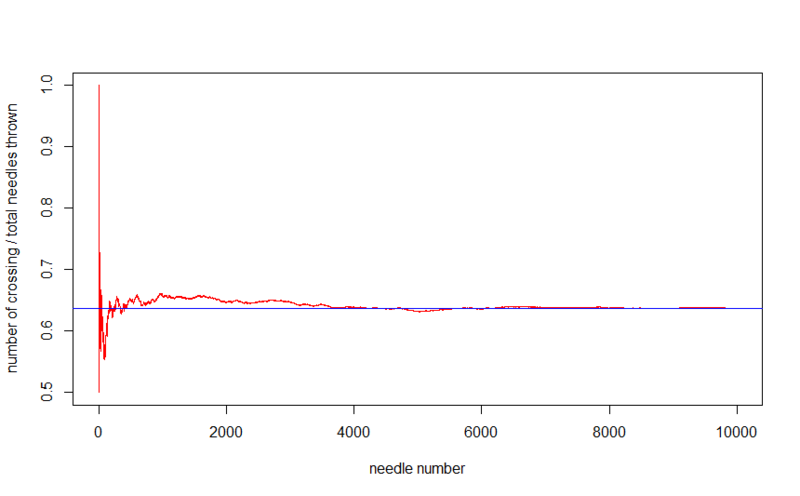
そして、次の変換を行います。デュースを結果のシリーズの各数で除算します。
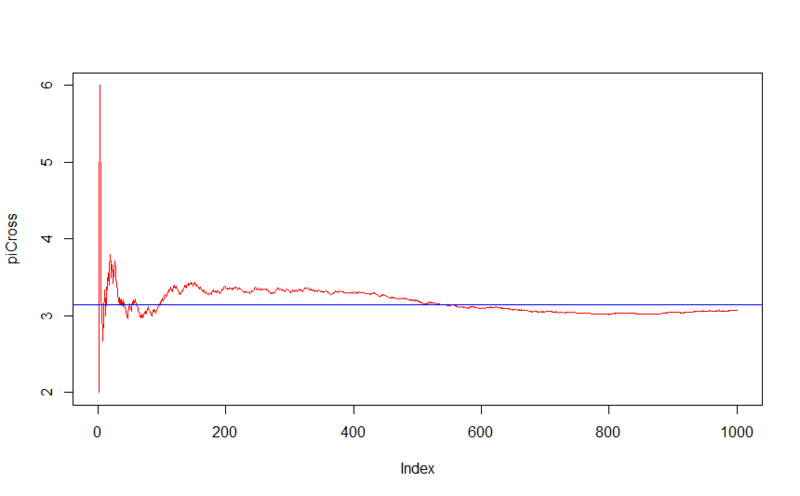
10,000本の針の場合、すでにより正確です。
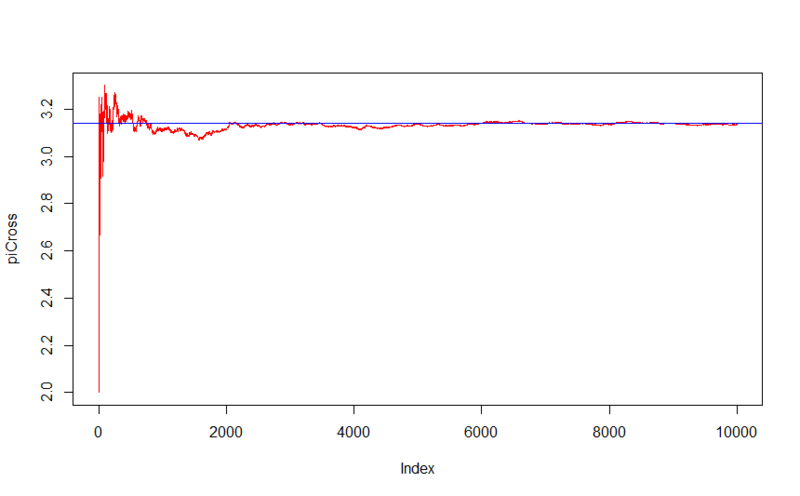
シリーズの最後の5,000人のメンバーの平均が見つかった場合、 3.1141685が得られますが 、piの数値は3.141593です。
一般的に、最後の行がPiに収束することは誰にとっても秘密ではありません。 しかし、これはどうして起こるのでしょうか？ これについては、前述のコースから28歳で学びました。 マタンに突入します。
理論
針と、それに最も近い右側の線を検討します。 針の左端からの距離はhで示され、線からの逸脱の角度はaです。
明らかに、角度aからの反対側の脚の長さは、角度のサインに斜辺の長さを掛けたものに等しくなります。 次に、 hが角度aの反対側の脚以下である場合、針は糸を横切ると主張できます。 グラフをプロットしましょう：
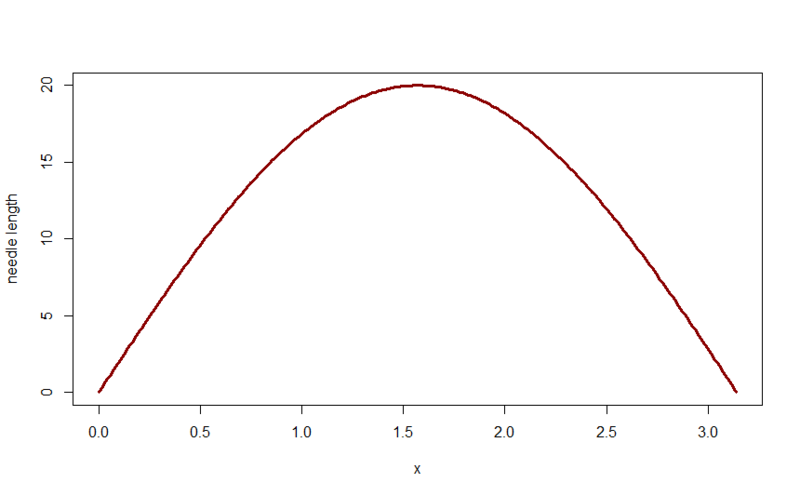
投げられた針ごとにhとaをカウントし、前のグラフでこれらの点をマークすると、図は次のようになります。
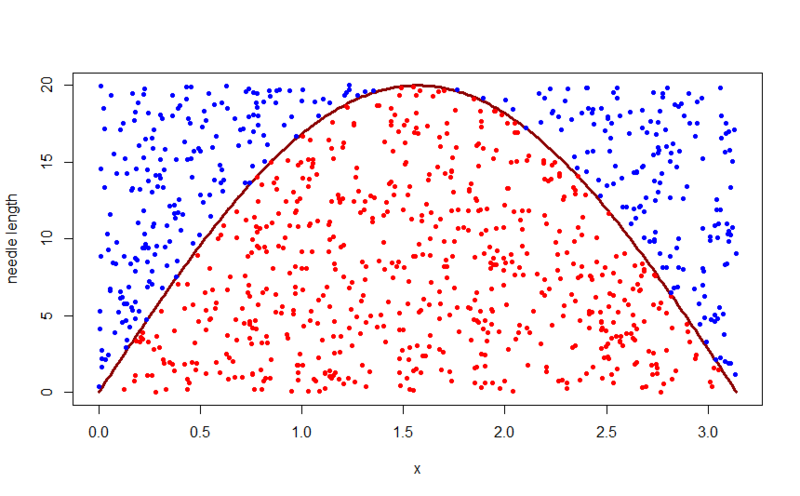
したがって、針が糸を横切る確率は、グラフの下の図形の面積と長方形の面積の比率、つまり、 Piに針の長さを掛けたものに等しくなります。
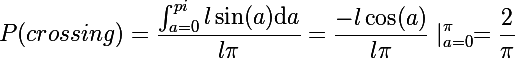
ここから、 Pi数の望ましい近似が得られます。これは、最初の部分の実験で示されました。