スイベル機構で署名を偽造します。 ケンペの定理

この投稿では、ヒンジ機構を使用して署名を偽るプログラムについて説明します。 このプログラムは、19世紀半ばに証明されたケンペの定理に基づいています。

ケンペの定理

技術の発展と列車の出現により、探究心は非常に興味深い問題を抱えていますが、円運動を直線運動に変換する、言い換えれば直線を描くヒンジ機構を作成することは可能です。 ヒンジ機構は、多数のスティックが固定されており、取り付けポイントで自由に回転できます。 多くの科学者はこの問題に取り組み、独創的なメカニズムを発明しましたが、すべて不正確な線を引きました。 たとえば、ワット、チェビシェフ、コイケンのメカニズムは次のとおりです。



多くの数学者は、理想的な直線を描くヒンジ機構を作成する問題は、19世紀半ばに正確な直線を描く独創的なリプキン-ポッセリエ機構が発見されるまで、原則として不溶性であると信じていました。



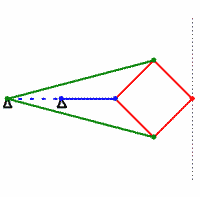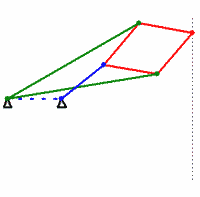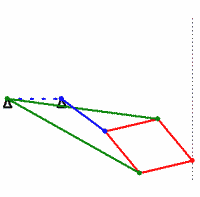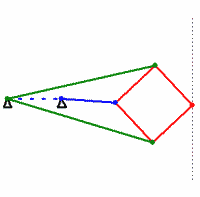
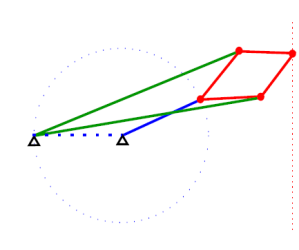
このメカニズムでは、同じ色のすべてのスティックの長さが同じです。 彼らが言うように、額で直接計算することで、メカニズムが本当に直線を描くことを証明できます。 しかし、反転変換に精通している人は、 証明でかなり明確なロジックを見ることができます。 Lipkin-Possellierメカニズムが発明された頃には、潤滑剤はすでに非常に優れていたため、テクノロジーの直線運動でこの理想的なトランスデューサーがなくてもできました。 結局のところ、ほぼ直線運動を別のワンドを通してピストンに伝達することが可能です。 このスティックは常にピストンガイドと完全に平行になるわけではありませんが、心配する必要はありません。 その結果、リプキン・ポッセリエ機構はテクノロジーに広く適用されることはありませんでしたが、数学に大きな影響を与えました。

数年後、数学者で弁護士のケンペは、この曲線だけを描くことができ、他には何もできない平面上の代数曲線の絶対的なメカニズムを構築する方法をアルゴリズムに与えます。 言い換えれば、動きが1自由度に制限されるメカニズムがあります。 この自由度に沿って移動すると、メカニズムは代数曲線を描きます。 この記事でケンペの優れた証拠を見つけました。 読者に、ケンペの定理で言及されている代数曲線は、方程式によって与えられる曲線であることを思い出させます。 どこで -任意の多項式。 例えば 半径の円です 、 -傾斜した直線、 -放物線。 ケンペはその証明で多くの興味深いアイデアを使用していますが、すでに知られているリプキン・ポッセリエ機構は重要な構築ツールです。

プロセス

ケンペの定理について学んだとたんに、私はすぐにユーザーが任意の曲線を描くことができるプログラムを書きたいと思いました。彼の署名は言うと、プログラムは代数曲線の署名を近似します ユーザーがコンピューターに何もインストールする必要がなく、サイトにアクセスしてすべてをワンクリックで実行できるように、Webアプリケーションを作成したかったのです。 私はプログラマーではないので、JavaScriptとHTML5に精通する良い機会でした。

ケンペの証明を学んだ後、私は非常に深刻な問題に直面しました。

代数曲線の署名を近似する方法 正確で、高速で、さらには遅いJavaScriptでもよいですか？ 図に示すように、曲線に沿って散らばった小さな円を組み合わせて、曲線を近似する非常に簡単ですが不適切な方法があります。



少しずつ 円は、多項式で定義されるため、明らかに代数曲線です。 どこで 円の中心であり、 -その半径。 すべての小さな円の結合は明らかに代数曲線になります。この結合は多項式で与えられるからです 。 しかし、ご覧のとおり、このタイプの近似は、自己交差点が非常に多いため、まったく適していません。 もっと「美しい」近似にしたいと思います。 「美しい」近似の問題は、数学的な観点と計算的な観点の両方から複雑であることがわかりました。 なんとなくこれを感じるために、代数曲線を想像することは有用です 表面を横断するような と飛行機 。 交差線は多項式係数に非常に敏感です 、完全に制御できないインコヒーレントで、分岐点を持ち、近似の「美しさ」を損なう可能性があります。

さまざまなアルゴリズムを1週間試した後、少なくとも何らかの形で曲線を近似しようとする私の試みはすべて無駄になりました。 すべてのアルゴリズムの動作は非常に遅く、不十分でした。 mathoverflowに関する質問を投稿した後、私はほとんどあきらめました。ここでは、伝統的に多くのプロの数学者が座っていました。 質問で、私はさりげなくヒンジで署名を偽造するためにこれが必要だと言いました。 数学者のミハイル・カポビッチが1日か2日で答えてくれたのは驚きでした。 彼は「眉ではなく、目で」と答えました。 判明したように、彼はかつてケンペの定理に取り組み、ジョン・ミルソンと一緒に、彼の記事で、代数曲線だけでなく、より自然に近似問題に適した曲線、すなわち曲線にもヒンジ機構を構築できることを証明しました多項式によりパラメトリックに定義されます：











このような曲線を使用すると、署名などの連続曲線を簡単に近似できます。 いわゆるチェビシェフ多項式を近似するか、最初にフーリエ級数を近似し、次にフーリエ級数の三角関数をテイラー級数に近似することができます。 曲線を代数曲線で近似しようとする代わりに、ケンペの証明自体を変更し、近似問題により適した曲線を構築できる関節機構を構築する方法を学ぶ方が良いことがわかります。

物語全体が巨大なダイヤモンドの発見のように感じました。 しかし、残念なことに、私はその記事を完全に理解していませんでした。 この記事は非常に難しいです。 しかし、私の問題の解決策があるという事実に目が開かれました。 ケンペの元の証明にわずかな変更を加えるだけで、コサイン三角曲線、つまり次の形の曲線を描くヒンジを構築できることがわかりました。











このような曲線を使用すると、Kapovich-Millsonの記事の曲線を使用するよりも、署名（フーリエ級数理論）を近似するのが簡単です。 実際、フーリエ級数の理論から、セグメント 機能 そして コサインで拡張できます。 近似精度のため 私たちが持っている：





オッズ そして 見つけやすい。 等式を左右に掛けるだけです 統合する 前に 、その後、右側では、項を持つものを除いて、ほぼすべての積分がゼロにリセットされます 最初の平等と用語で 第二に。 結果は次のとおりです。



このポストに、これらの三角曲線を構成するヒンジを構成するアルゴリズムを配置するかどうか、私は長い間考えていました。 それから、これはテキストに数学的な鈍さを加えることに気づきました。 人々は通常、この種のテキストの長い証拠を読むことを好みません。 したがって、 リンク （upd： mirror ）だけを使います。 好奇心の強い人は見ることができます。

そして実際には、署名を改ざんするアプリケーション自体があります： david.wf/linkage 。 （upd： mirror ）マウスでデザインを移動し、スクローラーを使用してズームインおよびズームアウトできることに注意してください（upd：近似の度合いは、特殊な「近似」スライダーでも変更できます）。 アプリケーションは最新のブラウザーで動作しますが、古いブラウザーではテストしませんでした。 クロムのみが他のブラウザ（ proflink ）よりもはるかに高速に直線を描画するため、クロムでは速度が遅くなります。 率直に言って、私は最適化に多大な労力を費やし、弱いコンピューターでは何も遅くならないようにしたが、率直に言って、私はあまり成功しなかった。 プログラムを構築するヒンジは、あなたの署名以外は何も描画できないことをもう一度強調します。 ヒンジは回転する青い三角形、つまり「エンジン」によって駆動されます。