上記のトピックに関する記事は、Habré全体で数件しか見つかりませんでした。 そして、トピックは優雅です。 そして先週の水曜日、コース「 計算ファイナンスと金融計量経済学入門 」はちょうど終わりました。 5週間目の記述統計に基づいて、この投稿が掲載されました。 参加者は面白くないでしょうが、 Rを使用したデータ分析の基本的なテクニックに精通したい人のために-habracatをお願いします。
予備協定
用語について
統計の作成者は、N年前に「ターバー」の学期しかありませんでした。 したがって、疑わしく翻訳された単語とその組み合わせの後、元の英語の用語が示されます（ カッコ内の斜体 ）。 スペシャリストは、個人でより正確な用語のバリエーションを送ってください。 ありがとう
インストールについて
ソフトウェアのインストールでは、些細なことを考慮して、意図的に注意が集中していません。 少なくともWindowsプラットフォームでは、標準の「next-> next-> ...-> ready」になりました。 記事で実行されるコードに必要な唯一のPerformanceAnalyticsパッケージは、「パッケージ/パッケージのインストール...」メニューからインストールされ、最も近いミラーを選択し、リストから目的のパッケージを選択します。
データセット
典型的なものを避けたかった：販売、アパート、在庫返品 （ 単純な返品 ）-私はいくらですか？ したがって、サンプルのサブジェクト領域は、Habrのコンテキストとそのコンテキスト外の両方で永遠です。 少し前のことですが、SamiKogoのブログは「あなたの胸はどれくらい大きいですか？」 無関係なオーディエンスを除外するための2つの回答オプションが含まれていることを考えると、サンプルの可能性にはある程度の自信があります。 便宜上、結果は次のとおりです。
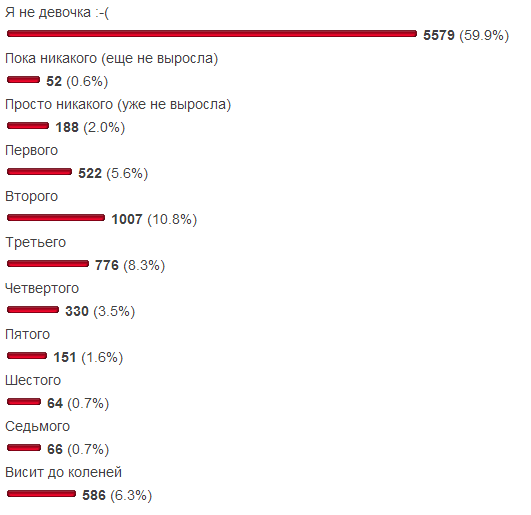
目的
ミニスタディでは、2つのデータセットの正規分布と比較します。
- （ND1）3番目（成長していない）から9番目（6番目のサイズ）までのオプション、
- （ND2）同じオプションですが、ゼロサイズに楽観主義者を追加し（まだ成長していません）、データに7番目のサイズを含めます。
経験豊富な統計学者にとっては、2番目のオプションを変更することにより、正規分布からの分布を放棄することは明らかです。 記事の終わりまでに、これを正式に正当化するのに十分な情報を蓄積しました。
研究の進捗
開始するには、データセットを変数に入れます。
data = c(rep(0, 184), rep(1, 510), rep(2, 996), rep(3, 763), rep(4, 327), rep(5, 147), rep(6, 60)) data_ol = c(data, rep(0, 51), rep(7, 65)) x.txt = " " #
関数cは引数を単一のベクトルに「接着」し、rep（x、y）関数はxのy値のベクトルを返します。 たとえば、rep（0、184）は、184個のゼロのベクトルを返します。 Googleの推奨事項や他のいくつかの情報源では、等号は割り当てに使用する価値はないという意見がありました。「<-」です。 知識のある人は、コメントに1文字ではなく2文字を書くために十分な理由を提供してください。 個人的には、著者にとって、この代替手段はPascal言語のoperator :: =に不便を与えます。
これで、ヒストグラムをプロットできます。
par(mfrow=c(1, 2)) hist(data, breaks=0:7, right=F, col="seagreen", main=" 1", xlab=x.txt, ylab=" ") hist(data_ol, breaks=0:8, right=F, col="slateblue1", main=" 2", xlab=x.txt, ylab=" ")
ヒストグラムを並べて表示するには、最初の行が必要です。 これがないと、2番目のヒストグラムが最初のヒストグラムを上書きします。 起こったことは次のとおりです。
アンケートを思い出しますよね？ 確かに、私たちの研究の特徴は、ヒストグラムに基づいてデータが生成されることです。 しかし、このステップには意味がないわけではありません。
- LJ非線形スケール（最初の回答の投票数による可能性が最も高い）。
- 両方のヒストグラムは同じスケールで描かれ、垂直方向に向けられています。これにより、 正規分布の確率密度（ 確率密度関数 ）と比較できます。
次のステップは、このような離散化されたデータセットに対してはほとんど意味がありません。 ここでは、サンプルからより「滑らかな」（読み取り、平均化）ヒストグラムを作成する密度関数に慣れるためにのみ説明します。
plot(density(data), type="l", col="seagreen", lwd=2, main=" 1") plot(density(data_ol), type="l", col="slateblue1", lwd=2, main=" 2")
結果：
サンプル分布パラメーターを計算します。
mu = mean(data) mu mu_ol = mean(data_ol) mu_ol var(data) var(data_ol) sig = sd(data) sig sig_ol = sd(data_ol) sig_ol library(PerformanceAnalytics) skewness(data) skewness(data_ol) kurtosis(data)# excess kurtosis (-3) kurtosis(data_ol)
結果：
| いいえ。ND | Mat.Waiting | 分散 | 標準偏差 | 非対称性（ 歪度 ） | 過剰（ 過剰尖度 ） |
|---|---|---|---|---|---|
| 1 | 2.408437 | 1.708542 | 1.307112 | 0.4124443 | 0.1001578 |
| 2 | 2.465034 | 2.17858 | 1.476001 | 0.7198767 | 0.7943986 |
表からわかるように、2番目のデータセットの変更
- 平均期待値をほとんど変えなかった、
- ランダム変数の広がりを増やし、
- ほぼ2倍で右側への分布の歪みが増加しました（右側の「テール」は分布密度で長くなりました）。
- （正規分布と比較して）「尾」の厚さがほぼ8倍に増加しました。
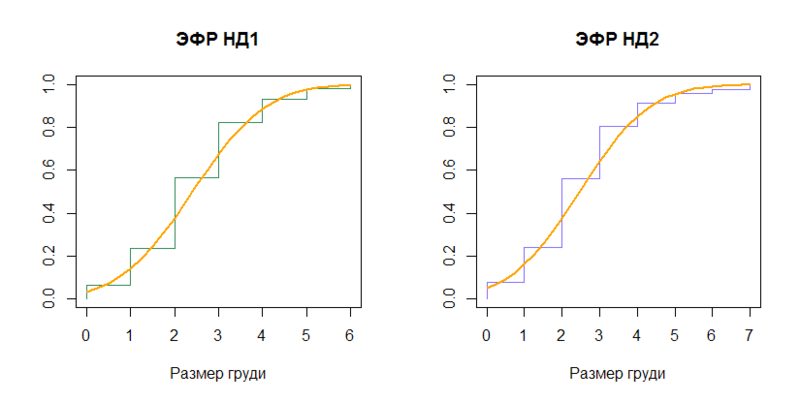
経験的分布関数（EGF）を対応する正規分布の累積分布関数 （N（2.408437、（1.307112） 2 ）およびN（2.465034、（1.476001） 2 ））と比較してみましょう。
n1 = length(data) plot(sort(data), (1:n1)/n1, type="S", col="seagreen", main=" 1", xlab=x.txt, ylab="") x = seq(0, 6, by=0.25) lines(x, pnorm(x, mean=mu, sd=sig), type="l", col="orange", lwd=2) n2 = length(data_ol) plot(sort(data_ol), (1:n2)/n2, type="S", col="slateblue1", main=" 2", xlab=x.txt, ylab="") x2 = seq(0, 7, by=0.25) lines(x2, pnorm(x2, mean=mu_ol, sd=sig_ol), type="l", col="orange", lwd=2)
結論：
分布関数から変位値、逆分布関数に渡します。
quantile(data) quantile(data_ol) qnorm(p=c(0, .25, .5, .75, 1), mean=mu, sd=sig) qnorm(p=c(0, .25, .5, .75, 1), mean=mu_ol, sd=sig_ol)
特定のケースでは、ステージはかなり退屈です。 サンプルの違いは100パーセンタイルのみです。
| 配布 | q 0 | q .25 | q .5 | q .75 | q 1 |
|---|---|---|---|---|---|
| ND1 | 0 | 2 | 2 | 3 | 6 |
| N（2.408437、（1.307112） 2 ） | -Inf | 1.526803 | 2.408437 | 3.290070 | Inf |
| ND2 | 0 | 2 | 2 | 3 | 7 |
| N（2.465034、（1.476001） 2 ） | -Inf | 1.469486 | 2.465034 | 3.460582 | Inf |
そして、ND1の四分位数が丸められていても正規分布のように見える場合、ND2は役に立ちません。
高度に離散化されたサンプルの分位数図（ 通常のQQプロット ）はあまり役に立ちません。 qqnorm関数を点灯するように言及しました。
qqnorm((data-mu)/sig, col="seagreen") abline( 0, 1, col="orange", lwd=2) qqnorm((data_ol-mu_ol)/sig_ol, col="slateblue1") abline( 0, 1, col="orange", lwd=2)
結果はエキサイティングに見えませんが、楽しいです：
そして、口ひげ （ boxplot ）で視覚的な結論ボックスのリストを完成させます 。
boxplot(data, outchar=T, main=" 1", ylab=x.txt) boxplot(data_ol, outchar=T, main=" 2", ylab=x.txt)
グラフィックス：
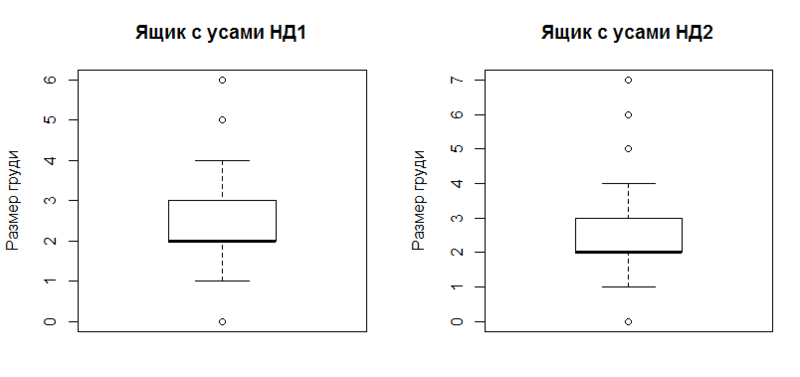
この構造は、サンプルの堅牢な特性を明確に反映しています（ 外れ値の存在に耐性があります）。
- 1番目と3番目の四分位（四角形の上限と下限）、
- 2番目の四分位数（中央値、水平線で太くなっています）、
- 信頼区間（上下の「ウィスカ」、これらの制限外のすべては排出とみなされます）、
- 実際、排出量（「口ひげ」の外側の円）。
この場合の信頼区間は、第1四分位から第3四分位から1.5四分位範囲までの偏差と見なされます。 詳細については?? Boxplot。
おわりに
ND1は、ND2未満の正規分布を念頭に置いています。
- 非対称性と過剰の低い値、
- サンプルの期待値とサンプルの標準偏差による分布の変位値の差は、サンプルの変位値と比較して小さい。
追加情報
Rの代替入門資料：
2番目と3番目のリンクは、公式ドキュメントの一部です。 偉大で強力な賢明な入門記事へのリンクがあれば、書いてください-私は付け加えます。
この記事の主な目的は、分析ツールとしてRに注目を集めることです。 知識のある人がより詳細な資料を提供してくれたら、私は心から喜んでそれを読んで楽しみます。
プルーフリーダー-PM。 残り-コメントへようこそ。
ご清聴ありがとうございました。