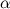🎇 🤭 🔈 有限離散分布を生成するためのインデックス手法 🍡 🙅🏻 🍼

ボーンスローをシミュレートすることは非常に興味深い場合があります。これを行うには、擬似乱数を使用して上面に値を生成できる効果的なアルゴリズムがありますアルファ

均一な分布から

。すなわち：

どこで

-引数の整数部分を取得します。

しかし、「不正な」骨があり、エッジが不均一に抜けるとします。骨にK面を持たせ、 p_i

顔の確率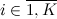

。そうすることで、自然な制限

。このような分布で擬似ランダムシーケンスをシミュレートする方法の質問に答えようとします。

#Naive approach len<-10 ps<-seq(len,2, by=-1) ps<- 1/ps^2 ps<-ps/sum(ps) ss<-cumsum(ps) gen_naiv <- function() { alpha<-runif(1) return (min(which(alpha<ss))) } #sample val<-c() len<-10000 for(i in 1:len) { val<-append(val, gen_naiv()) } vals<-factor(val) plot(vals)

このような配布を生成する「単純な」バージョンを検討してください。部分和の概念を紹介します

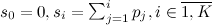、平等を書き出すことができます

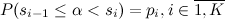。知られているまま

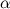そして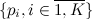

特定のiを見つける。 1から始まりKで終わるすべてのiを単純に反復する場合、平均して

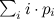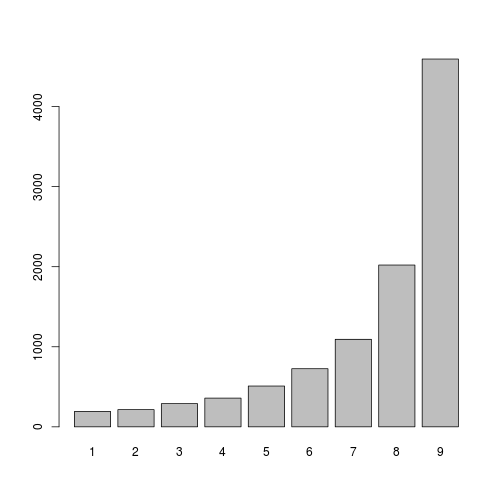
比較操作。最悪の場合、偶然に確率で発生します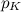

、Kの比較が必要です。たとえば、上のグラフから、0.45473749の確率で発生します。平均して、7.5回の比較と1つのランダム変数の生成が必要です。操作の数は、特に間違ったボーンで多数のスローをシミュレートする必要がある場合に悲しくなります。

問題を解決する方法の1つは、そのような正しいボーンをピックアップすることです。それを見ると、おおよその間違ったボーンを近似し、非常に迅速に実行できます。このメソッドはChenメソッドと呼ばれ、「カットポイントメソッド」または「インデックス検索」メソッドという名前で見つけることもできます。

メソッドの本質は非常にシンプルで、セグメントを分割します [0,1]

M個の等しい部分に。長さMの追加の配列rを導入します。 r_j

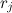配列は次のようにiに保存されます

：

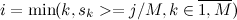 #Preprocessing ss<-cumsum(ps) ss<-append(ss, 0, after=0) M<-length(ss) rs<-c() for(k in 0:(M-1)) rs<-append(rs, min(which(ss>=k/M)))

この場合、新しい値を生成するアルゴリズムは次の形式を取ります。

 #chen's method finite discrete distribution generator gen_dfd <- function() { M<-10 alpha<-runif(1) idx<-rs[floor(alpha*M)+1] return (idx-1+min(which(alpha<ss[idx:(M+1)]))-1) } #sample code val<-c() len<-10000 for(i in 1:len) { val<-append(val, gen_dfd()) } vals<-factor(val) plot(vals)

最悪の場合、上記の例では、0.03712143の確率で4つの比較が必要です（Mは9）。平均して、1つのランダム変数と1.2の比較を生成する必要があります。大量のメモリとデータ準備の段階がある場合（タスク p_i

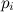）は比較的まれで、Mは任意に大きく選択できます。

この方法は実装が簡単で、特に多数のほぼ同一の状態の場合に、同じランダム変数の多数の実装を生成する速度を大幅に向上させます。念のため、 pastebinにはc ++での近似実装が配置されています。

有限離散分布を生成するためのインデックス手法

More articles: