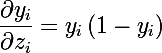を使用して
ここでは、すべての表記法、インターフェース、および学習アルゴリズム自体が変更なしで使用されるため、 以前の投稿をよく理解することをお勧めします。
ソフトマックス活性化機能
したがって、私たちが直面する最初のタスクは、ネットワークが確率分布をモデル化する方法を提供することです。 これを行うには、次のような直接配布ネットワークを作成します。
- ネットワークには多くの隠れ層が含まれ、すべてのニューロンは独自の活性化機能を持つことができます。
- 最後の層には、クラスの数に対応するそのような数のニューロンがあります。 これらのニューロンはすべて、ソフトマックスレイヤーまたはグループと呼ばれます。
Softmaxグループのニューロンには、 次の活性化機能があります (このセクションでは、レイヤーインデックスを省略します。これは最後であり、 n個のニューロンが含まれることを意味します)。
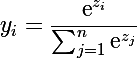 i番目のニューロン
i番目のニューロン
式から、各ニューロンの出力はsoftmaxグループの他のすべてのニューロンの加算器に依存し、グループ全体の出力値の合計は1であることがわかります。 この関数の利点は、加算器のi番目のニューロンの偏導関数が次と等しいことです。
前の記事の IFunctionインターフェイスを使用して、この関数を実装します。
softmax関数を実装する
メソッドの実装は、softmaxレイヤーの実装でグループの出力値を計算する方が安価であるため、通常は必要ないことに注意してください。 しかし、完全を期すために、万が一の場合に備えて、-)
double Compute(double x)
メソッドの実装は、softmaxレイヤーの実装でグループの出力値を計算する方が安価であるため、通常は必要ないことに注意してください。 しかし、完全を期すために、万が一の場合に備えて、-)
internal class SoftMaxActivationFunction : IFunction { private ILayer _layer = null; private int _ownPosition = 0; internal SoftMaxActivationFunction(ILayer layer, int ownPosition) { _layer = layer; _ownPosition = ownPosition; } public double Compute(double x) { double numerator = Math.Exp(x); double denominator = numerator; for (int i = 0; i < _layer.Neurons.Length; i++) { if (i == _ownPosition) { continue; } denominator += Math.Exp(_layer.Neurons[i].LastNET); } return numerator/denominator; } public double ComputeFirstDerivative(double x) { double y = Compute(x); return y*(1 - y); } public double ComputeSecondDerivative(double x) { throw new NotImplementedException(); } }
エラー機能
各トレーニングの例では、必要な確率分布をモデル化したネットワーク出力を取得し、2つの確率分布を比較するための正しい測定が必要です。 クロスエントロピーはそのような尺度として使用されます:

- t-現在のトレーニング例に必要な出力
- y-ニューラルネットワークの実出力
一般的なネットワークエラーは次のように計算されます。

モデル全体の優雅さを実現するには、出力次元の1つまたはニューロンから勾配がどのように計算されるかを確認する必要があります。 「出力層」セクションの以前の投稿で、タスクはdC / dz_iの計算に限定されると説明されていますが、これからも続けます。
 なぜなら 各ニューロンの出力には電流の加算器が含まれているため、全体の量を区別する必要があります。 コスト関数はニューロンの出力のみに依存し、出力は加算器のみに依存するため、2つの偏導関数に分解できます。 次に、合計の各メンバーを個別に検討します(主なことは、インデックスに注意を払うことです。この場合、 jはグループのsoftmaxニューロンを通り、 iは現在のニューロンです)
なぜなら 各ニューロンの出力には電流の加算器が含まれているため、全体の量を区別する必要があります。 コスト関数はニューロンの出力のみに依存し、出力は加算器のみに依存するため、2つの偏導関数に分解できます。 次に、合計の各メンバーを個別に検討します(主なことは、インデックスに注意を払うことです。この場合、 jはグループのsoftmaxニューロンを通り、 iは現在のニューロンです) 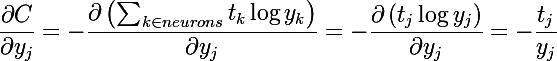



最後の変換は、softmaxグループのニューロンの特性に従って、出力ベクトルの値の合計が1に等しくなければならないという事実により得られます。 これは、トレーニングサンプルの重要な要件です。そうしないと、勾配が正しく計算されません。
前と同じ表現を使用して実装に進みます。
クロスエントロピーの実装
internal class CrossEntropy : IMetrics<double> { internal CrossEntropy() { } /// <summary> /// \sum_i v1_i * ln(v2_i) /// </summary> public override double Calculate(double[] v1, double[] v2) { double d = 0; for (int i = 0; i < v1.Length; i++) { d += v1[i]*Math.Log(v2[i]); } return -d; } public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index) { return v2[v2Index] - v1[v2Index]; } }
ソフトマックス層
一般的に、特別なレイヤーを行う必要はありません。上記のアクティベーション関数を使用して通常の直接配信ネットワークのコンストラクターに最後のレイヤーを作成し、コンストラクターでsoftmaxレイヤーへのリンクを渡すだけで、各ニューロンの出力を計算するたびに関数の分母が計算されますただし
double[] ComputeOutput(double[] inputVector)
ニューラルネットワークの
double[] ComputeOutput(double[] inputVector)
適切に実装する場合:
public double[] ComputeOutput(double[] inputVector) { double[] outputVector = inputVector; for (int i = 0; i < _layers.Length; i++) { outputVector = _layers[i].Compute(outputVector); } return outputVector; }
その後、ネットワークはニューロンのComputeメソッドを直接呼び出すのではなく、この関数をレイヤーに委任するため、活性化関数の分母を一度計算することができます。
ソフトマックス層
internal class SoftmaxFullConnectedLayer : FullConnectedLayer { internal SoftmaxFullConnectedLayer(int inputDimension, int size) { _neurons = new INeuron[size]; for (int i = 0; i < size; i++) { IFunction smFunction = new SoftMaxActivationFunction(this, i); _neurons[i] = new InLayerFullConnectedNeuron(inputDimension, smFunction); } } public override double[] Compute(double[] inputVector) { double[] numerators = new double[_neurons.Length]; double denominator = 0; for (int i = 0; i < _neurons.Length; i++) { numerators[i] = Math.Exp(_neurons[i].NET(inputVector)); denominator += numerators[i]; } double[] output = new double[_neurons.Length]; for (int i = 0; i < _neurons.Length; i++) { output[i] = numerators[i]/denominator; _neurons[i].LastState = output[i]; } return output; } }
まとめ
そのため、不足している部分は準備ができており、 コンストラクタを組み立てることができます。 たとえば、 コンストラクターが異なるだけで、同じ直接配信ネットワーク実装を使用します。
コンストラクターの例
/// <summary> /// Creates network with softmax layer at the outlut, and hidden layes with theirs own activation functions /// </summary> internal FcMlFfNetwork(int inputDimension, int outputDimension, int[] hiddenLayerStructure, IFunction[] hiddenLayerFunctions, IWeightInitializer wi, ILearningStrategy<IMultilayerNeuralNetwork> trainingAlgorithm) { _learningStrategy = trainingAlgorithm; _layers = new ILayer[hiddenLayerFunctions.Length + 1]; _layers[0] = new FullConnectedLayer(inputDimension, hiddenLayerStructure[0], hiddenLayerFunctions[0]); for (int i = 1; i < hiddenLayerStructure.Length; i++) { _layers[i] = new FullConnectedLayer(_layers[i - 1].Neurons.Length, hiddenLayerStructure[i], hiddenLayerFunctions[i]); } //create softmax layer _layers[hiddenLayerStructure.Length] = new SoftmaxFullConnectedLayer(hiddenLayerStructure[hiddenLayerStructure.Length - 1], outputDimension); for (int i = 0; i < _layers.Length; i++) { for (int j = 0; j < _layers[i].Neurons.Length; j++) { _layers[i].Neurons[j].Bias = wi.GetWeight(); for (int k = 0; k < _layers[i].Neurons[j].Weights.Length; k++) { _layers[i].Neurons[j].Weights[k] = wi.GetWeight(); } } } }