最新のコンピュータービジョンアルゴリズムの多くは、視覚画像の特定のポイントの検出と比較に基づいています。 Habréのこのトピックに関して多くの記事が書かれています（たとえば、 SURF 、 SIFT ）。 しかし、ほとんどの作品は、画像間の誤った一致をフィルタリングするような重要な段階に十分な注意を払っていません。 ほとんどの場合、 RANSACメソッドはこれらの目的に使用され、ここで停止します。 しかし、これがこの問題を解決する唯一のアプローチではありません。
この記事では、誤った一致をフィルタリングするための代替方法の1つに焦点を当てています。
問題の声明
それぞれn p点とn q点の2つの画像PとQから得られた特異点の2つのセットがあるとします。各特異点はペアp = {p d 、p c }です。 p d-ポイントのローカルフィーチャ（たとえば、SURF記述子）であり、p c = {x、y}はフィーチャポイントの座標です。
多くの対応がありますM = {c i =（i、i '）| c i∈C、i∈P、i '∈Q}、何らかのメトリックを使用して構築されます（たとえば、ユークリッドメトリックに最も近い記述子を持つポイントとして）。 各対応について、非負の推定関数S c i = f 1 （i d 、i ' d ）を構築します。
2つの対応c i =（i、i '）およびc j =（j、j'）について、最初の画像の点iとjと2番目の画像の点i 'とj' l ijとl i ' j '、それぞれ。 明らかに、これら2つの一致が真である場合、スケール係数l ij fraslで画像QをPに揃えることができます。 l i'j ' 、このペアの一致はスケールl ij fraslに投票すると言います。 l i'j ' ここで、それに対応するn個の正しい一致がある視覚画像があり、これらの一致の各ペアについて、スケールファクターがほぼ同じであると仮定します。 このようなスケールは、幾何学的整合性のスケール係数と呼ばれ、sで示されます。 一致ペアc i =（i、i '）およびc j =（j、j'）の幾何学的整合性のスケールファクターは、次のように表されます。
S c i c j （s）= f 2 （| l ij -s * l i'j ' |）、ここでf 2 （x）は非負の単調減少関数です。
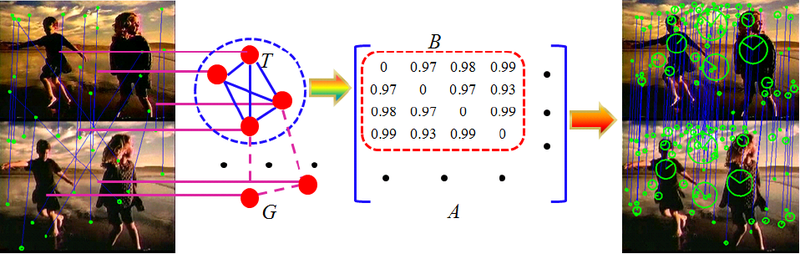
セットMにm個の対応M = {c 1 、...、c m }が含まれているとします。 m個の頂点を持つグラフGを作成します。各頂点はMからの対応を表します。頂点iとjの間のエッジの重みは次のように定義されます。
w ij （s）= S c i * S c j * S c i c j （s）。
このようにして構築されたグラフは、動的コレスポンデンスグラフ（以下、DGSと呼びます）と呼ばれます。
DGSの重み付き隣接行列をA（s）で示し、次のように構築します。
A（s）∈R m * m-対称かつ非負。
n個の特異点を含む正しい視覚画像は、n個の頂点を持つ完全な部分グラフT∈Gに対応します。これは、簡単にわかるように、最大クリークの重み付き複製です。 このようなサブグラフは、クラスタ内の平均スコアが高くなっています。
Tを次のようなインジケーターベクトルyとして表す場合
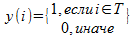、その後、クラスタ内の平均推定値を2次形式で書き換えることができます。
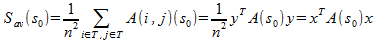どこで 
、 
。
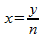知られているように、Motzkin-Straussの定理は、そのような2次形式の最大クリークと局所最大値の間の接続を確立します。
どこで 
R mの標準シンプレックスです。 簡単に言えば、定理は、グラフGの頂点のサブセットTは、その特性ベクトルx Tが標準シンプレックスの2次関数f（x）の局所最大値である場合にのみ最大クリークであると言います。 i∈Tの場合、x i T = 0それ以外の場合。
元のMotzkin-Straussの定理は重み付けされていないグラフのみに関係しますが、PavanとPelilloはそれを重み付けされたグラフに一般化し、密な部分グラフと方程式の局所的最大値との関係を確立しました。
受け入れられている規範l 1にはいくつかの利点があります。 第一に、それは単純な確率的意味を持ちます：x iは完全な部分グラフに頂点iが含まれる確率を表します。 次に、解xはまばらであり、同じサブグラフ内の一部のコンポーネントのみが非常に重要であり、残りのコンポーネントは非常に小さいため、ノイズである頂点を破棄することでクラスターを分離できます。
したがって、対応関係をフィルタリングするタスクは、個々の視覚画像を表す対応関係のクラスターを見つける問題に縮小されます。 次に、このようなクラスターを見つけるために、上記の最適化問題を解決する必要があります。
アルゴリズムの説明
スケールs 0の場合、最適化問題
多くの局所的最大値を持つことがあります。 ほとんどの場合、各大きな極大値は正しい視覚画像に対応し、小さな極大値はノイズの結果として最も頻繁に発生します。
x（1）を初期化するとき、対応する局所解xは、次の形式の1次自己組織化方程式を使用して効果的に取得できます。
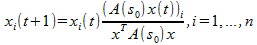
シンプレックスΔは、このようなダイナミクスに関して不変であることに注意できます。これは、Δで始まる軌道がΔに残ることを意味します。 さらに、A（s 0 ）が対称で非負の要素を持つ場合、目的関数
自己組織化方程式の一定でない軌道に沿って厳密に増加し、これらの漸近的に安定した点は、二次関数の局所解と厳密に1対1に対応しています。
大まかに言って、xのすべての大きな局所最大値を見つけるために、多くの初期初期化を行い、したがって、指定されたシンプレックスでのすべての大きな局所最大値が考慮されることを保証します。 前述のように、タスクの場合、各極大値は視覚画像に対応し、次の2つのプロパティが必要です。
- 局所性プロパティ。 1つの視覚画像の特異点は小さな近傍にあるため、GVDの各頂点の近傍でのみx（1）を初期化する必要があります。
- 交差しないプロパティ。 原則として、異なる視覚画像にはGの共通の頂点は含まれません。つまり、2つの局所的な最大値xとyが2つの異なる視覚画像に対応する場合、（x、y）〜0です。
DGSの各頂点に対してx（1）を初期化し、同じ視覚画像の頂点の初期化は約1つの局所最大値に収束するため、同じ視覚画像に対応する局所最大値をマージする必要があります。 このようなデータの冗長性により、追加のノイズ耐性が実現されます。 ノイズに対応する小さな極大値もすべて破棄されます。
最後に、各局所最大xの視覚画像を復元する必要があります。 なぜなら x iは、頂点iが視覚画像xに入る確率を表します。視覚画像に出現する可能性が最も高い頂点のみを選択できます。
アルゴリズムパラメーター
上記の説明からわかるように、アルゴリズムには次のような多数の構成可能なパラメーターがあります。
- S c i = f 1 （i d 、i ' d ）-適合性評価関数
- S c i c j （s）= f 2 （| l ij -s * l i'j ' |）-対応の幾何学的整合性を評価するための関数
- Ε-初期化の近傍に属するためのrib骨の重量を推定するためのしきい値
- Φは、初期化x（1）が行われる近傍の半径です
- Ψ-極大値の小ささを評価するためのしきい値
- Ω-近傍をマージするためのしきい値
- Θ-頂点が視覚画像に入る確率のしきい値
実験
アルゴリズムの典型的な結果を以下に示します。
おわりに
説明されたアルゴリズムの実用的な適用は、入力データの各セットに対して経験的に選択されたアルゴリズムのパラメーターに対する感度が高いため困難です。 また、この方法を効果的に適用するには、支配的なスケール係数の割り当てに対応する入力セットの予備分析が必要です。
データの冗長性が原因でノイズとの戦いが発生するという事実により、アルゴリズムには大量の追加メモリと処理時間が必要です。
したがって、このアルゴリズムは、記事の冒頭で言及したRANSACメソッドの代替としてではなく、対応分析に使用されるアプローチの観点から興味深いものです。
文学
- 空間的にコヒーレントな対応を介した共通の視覚パターンの発見Hairong Liu、Shuicheng Yan、電気およびコンピューターエンジン部門、シンガポール国立大学、シンガポール
- T.モツキンとE.ストラウス。 グラフのマキシマとトゥランの定理の新しい証明。 カナッド。 J. Math、1965。
- 10. M. Pelillo、K。Siddiqi、およびS. Zucker。 関連グラフを使用した階層構造の一致。 TPAMI、1999。
メソッドソースへのUPDリンク： dl.dropbox.com/u/15642384/src.7z