私の過去の投稿の1つでバランスのとれた検索ツリーを構築するためのかなり現代的なアプローチであった場合、この投稿はAVLツリーの実装に専念します -おそらく、ソ連の科学者アデルソンによって1962年に発明された最初のタイプのバランスのとれたバイナリ検索ツリー-ウェルスキーとランディス。 ネットワーク上でAVLツリーの多くの認識を見つけることができます（たとえば、 ここ ）が、特にすべてをゼロから理解しようとしている場合、私が個人的に見たすべてが楽観主義を刺激することはありません。 どこでも、AVLツリーは赤黒ツリーよりも単純であると主張されていますが、これに添付されているコードを見ると、このステートメントを疑うようになります。 実際、AVLツリーがどのように配置されているかを指で説明したいという欲求が、この投稿を書く動機になりました。 プレゼンテーションはC ++コードで示されています。

AVLツリーの概念

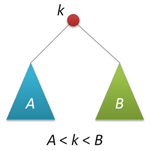AVLツリーは、まず、バイナリ検索ツリーであり、そのキーは標準プロパティを満たします。ツリーノードのキーは、このノードの左サブツリーのキー以上であり、このノードの右サブツリーのキー以下です。 つまり、標準のアルゴリズムを使用して、AVLツリーで目的のキーを検索できます。 簡単にするために、ツリー内のすべてのキーは整数であり、繰り返されないと仮定します。



AVLツリーの特徴は、次の意味でバランスが取れていることです。 ツリーノードの場合、その右サブツリーの高さと左サブツリーの高さの差は1以下です。 このプロパティは、ツリーの高さがそのノードの数に対数的に依存するのに十分であることが証明されています：nキーを持つAVLツリーの高さhは、log ₂ （n + 1）から1.44 log ₂ （n + 2）-0.328の範囲にあります。 また、バイナリ検索ツリーの基本操作（ノードの検索、挿入、削除）はその高さに線形に依存するため、これらのアルゴリズムの動作時間のツリーに格納されているキーの数に対する対数依存性が保証されます。 ランダム化された検索ツリーは、確率的な意味でのみバランスを提供することを思い出してください。大きなnに対して非常にアンバランスなツリーを取得する確率は、無視できますが、 非ゼロのままです 。

ノード構造

次の構造でAVLツリーのノードを表します。

struct node //      { int key; unsigned char height; node* left; node* right; node(int k) { key = k; left = right = 0; height = 1; } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

キーフィールドにはノードキーが格納され、高さフィールドには特定のノードのルートを持つサブツリーの高さが、左および右フィールドには左および右サブツリーへのポインタが格納されます。 単純なコンストラクターは、指定されたキーkで新しいノード（高さ1）を作成します。



従来、AVLツリーのノードは高さを格納しませんが、右と左のサブツリーの高さの差（いわゆるバランスファクター）は3つの値-1、0、1のみを取ることができます。ただし、この差は変数に格納されます。そのサイズは少なくとも1バイトに等しい（そのような値の「効果的な」パッケージングのトリッキーなスキームを考え出さない限り）。 高さh <1.44 log ₂ （n + 2）、つまり、n = 10 ⁹ （10億個のキー、ノードを格納するための10ギガバイト以上のメモリ）の場合、ツリーの高さはh = 44を超えないことを思い出してくださいバランス係数と同じ1バイトのメモリに正常に配置されました。 したがって、高さを保存しても、ツリーノードに割り当てられるメモリ量は増加しませんが、一方では、一部の操作の実装が大幅に簡素化されます。



高さに関連する3つの補助関数を定義します。 最初は高さフィールドのラッパーで、nullポインター（空のツリー）で動作します：

 unsigned char height(node* p) { return p?p->height:0; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2番目は、指定されたノードのバランス係数を計算します（ゼロ以外のポインターでのみ機能します）。

 int bfactor(node* p) { return height(p->right)-height(p->left); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

3番目の関数は、指定されたノードの高さフィールドの正しい値を復元します（右および左の子ノードのこのフィールドの値が正しい場合）。

 void fixheight(node* p) { unsigned char hl = height(p->left); unsigned char hr = height(p->right); p->height = (hl>hr?hl:hr)+1; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

3つの関数はすべて再帰的ではないことに注意してください。 それらの動作時間はO（1）の値です。

ノードバランシング

AVLツリーでノードを追加または削除するプロセスでは、一部のノードのバランスファクターが2または-2であることが判明する場合があります。 サブツリーの不均衡があります。 状況を修正するために、特定のツリーノードの周囲で既知のターンが使用されます。 右（左）への単純な回転により、次のツリー変換が生成されることを思い出させてください。







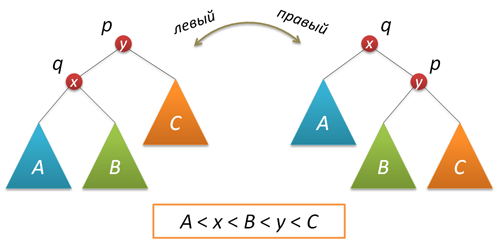
右折を実装するコードは次のようになります（通常、ツリーを変更する各関数は、結果のツリーの新しいルートを返します）。

 node* rotateright(node* p) //    p { node* q = p->left; p->left = q->right; q->right = p; fixheight(p); fixheight(q); return q; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

左ターンは、右の対称コピーです。

 node* rotateleft(node* q) //    q { node* p = q->right; q->right = p->left; p->left = q; fixheight(q); fixheight(p); return p; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、ノードpの右サブツリーの高さが左サブツリーの高さより2大きい場合の不均衡状況を考えてみましょう（反対のケースは対称的であり、同様に実装されます）。 qをノードpの右の子、sをノードqの左の子にします。







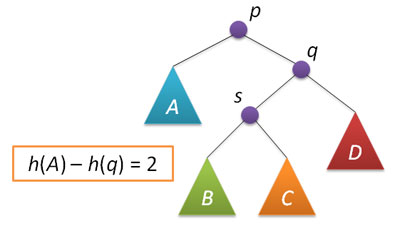
この状況のフレームワーク内の可能なケースの分析は、ノードpの不均衡を修正するために、pの単純な左折または同じpのいわゆる大左折を実行することで十分であることを示します。 ノードqの左サブツリーの高さがその右サブツリーの高さよりも大きい場合、単純な回転が実行されます：h（s）≤h（D）。







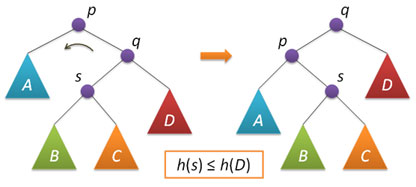
h（s）> h（D）の条件下で大きな回転が適用され、この場合は2つの単純な回転に削減されます-最初はqを中心とした右回転、次にpを中心とした左回転です。







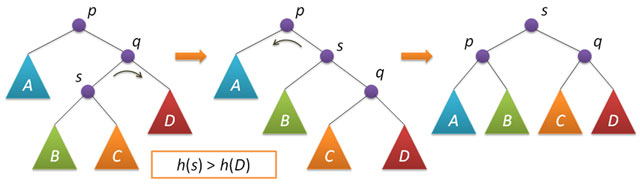
バランシングを実行するコードは、条件の確認と順番の決定に帰着します。

 node* balance(node* p) //   p { fixheight(p); if( bfactor(p)==2 ) { if( bfactor(p->right) < 0 ) p->right = rotateright(p->right); return rotateleft(p); } if( bfactor(p)==-2 ) { if( bfactor(p->left) > 0 ) p->left = rotateleft(p->left); return rotateright(p); } return p; //    }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

記載されている回転とバランスの機能には、サイクルや再帰も含まれていません。つまり、AVLツリーのサイズに関係なく、一定の時間実行されます。

キー挿入

新しいキーは、単純な検索ツリーと同じ方法で、概してAVLツリーに挿入されます。現在のノードのキーと挿入されるキーを比較した結果に応じて、ツリーを下って移動の右または左の方向を選択します。 唯一の違いは、再帰から戻るとき（つまり、キーが右または左のサブツリーに挿入され、このツリーが平衡化された後）、現在のノードが平衡化されることです。 パスに沿った任意のノードでのこのような挿入から生じる不均衡は2を超えないことが厳密に証明されます。これは、上記のバランス機能の適用が正しいことを意味します。

 node* insert(node* p, int k) //   k     p { if( !p ) return new node(k); if( k<p->key ) p->left = insert(p->left,k); else p->right = insert(p->right,k); return balance(p); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

実装された挿入アルゴリズムとAVLツリーの高さの理論的推定値との対応を確認するために、簡単な計算実験が行われました。 1〜10,000のランダムに配置された番号から配列が生成され、これらの番号が最初に空のAVLツリーに連続して挿入され、各挿入後にツリーの高さが測定されました。 結果は1000回の計算で平均されました。 次のグラフは、平均高さのnへの依存性を示しています（赤線）。 最小の高さ（緑の線）; 最大高さ（青い線）。 さらに、上限および下限の理論的推定値が示されています。







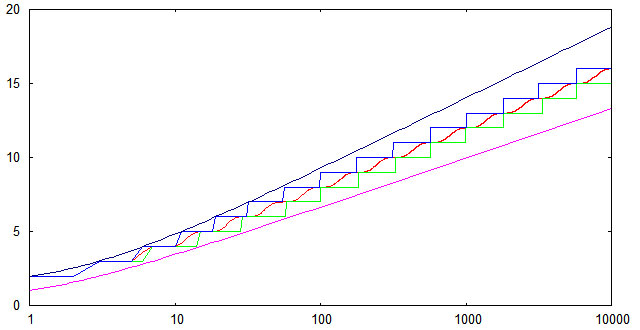
キーのランダムシーケンスの場合、実験的に検出された高さはわずかなマージンがあっても理論上の境界に収まることがわかります。 元のキーシーケンスが昇順で順序付けられている場合、下限は（少なくともいくつかのポイントで）達成可能です。

キーの削除

残念ながら、AVLツリーからノードを削除すると、ランダム検索ツリーのようにすべてがチョコレートではなくなります。 2つのツリーのマージ（結合）に基づくメソッドで、検出も発想もされません。 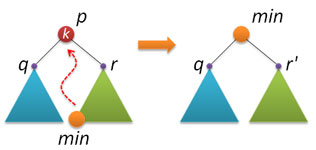そのため、ほぼすべての場所で説明されたオプションが採用されました（通常、標準のバイナリ検索ツリーからノードを削除するときに使用されます）。 アイデアは次のとおりです。特定のキーkを持つノードpを見つけ（見つからない場合は何もする必要はありません）、正しいサブツリーで最小のキーを持つminノードを見つけ、削除されたノードpを見つかったminノードに置き換えます。



実装時には、いくつかの微妙な違いがあります。 まず、見つかったノードpに右側のサブツリーがない場合、左側のAVLツリーのプロパティにより、このノードは単一の子ノード（高さ1のツリー）のみを持つことができます。または、一般にノードpはリーフです。 どちらの場合でも、ノードpを削除し、結果としてノードpの左の子ノードへのポインターを返すだけです。



ここで、pに正しいサブツリーを持たせます。 このサブツリーで最小キーを見つけます。 バイナリ検索ツリーのプロパティにより、このキーはツリーのルートから開始して、左ブランチの最後に配置されます。 再帰関数を使用します。

 node* findmin(node* p) //        p { return p->left?findmin(p->left):p; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

別のユーティリティ機能は、指定されたツリーから最小要素を削除することです。 繰り返しになりますが、AVLツリーのプロパティにより、右側の最小要素には単一ノードが中断されているか、そこで空になっています。 どちらの場合も、正しいノードにポインターを返し、戻りの途中で（再帰から戻るときに）バランスを取る必要があります。 最小ノード自体は削除されません。 彼はまだ私たちにとって有用です。

 node* removemin(node* p) //        p { if( p->left==0 ) return p->right; p->left = removemin(p->left); return balance(p); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これで、AVLツリーからのキーの削除を実装する準備がすべて整いました。 まず、目的のノードを見つけ、キーを挿入するときと同じアクションを実行します。

 node* remove(node* p, int k) //   k   p { if( !p ) return 0; if( k < p->key ) p->left = remove(p->left,k); else if( k > p->key ) p->right = remove(p->right,k);
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

キーkが見つかったら、プランBに進みます。ノードpの左右のサブツリーのルートqとrを思い出してください。 ノードpを削除します。 右のサブツリーが空の場合、左のサブツリーへのポインタを返します。 右のサブツリーが空でない場合は、そこから最小要素minを見つけ、そこからそれを抽出し、qを左からminに掛け、rから右になったものを、バランスをとってからminを返します。

  else // k == p->key { node* q = p->left; node* r = p->right; delete p; if( !r ) return q; node* min = findmin(r); min->right = removemin(r); min->left = q; return balance(min); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

再帰を終了するときは、バランスを取ることを忘れないでください：

  return balance(p); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

それだけです！ 最小ノードの検索とその抽出は、原則として1つの関数に実装でき、関数からポインターのペアを返す（それほど難しくない）問題を解決する必要があります。 ただし、適切なサブツリーで1つのパスで保存できます。



明らかに、挿入操作と削除操作（および単純な検索操作）は、ツリーの高さに比例した時間で実行されます。 これらの操作を実行するプロセスでは、ルートから特定のノードへの降下が実行され、各レベルで特定の固定数のアクションが実行されます。 また、AVLツリーのバランスが取れているという事実により、その高さはノードの数に対数的に依存します。 したがって、3つの基本操作すべての実行時間は、ツリーノードの数に対数的に依存することが保証されています。



ご清聴ありがとうございました！

ソース

• B. Pfaff、バイナリ検索ツリーとバランスツリーの紹介-libavlライブラリの説明
• N. Wirth、アルゴリズムとデータ構造-Virtによるバランスの取れたツリー-これらは単なるAVLツリーです
• T. Kormen et al。、Algorithms：construction and analysis- ABLツリーは、赤黒ツリーに関する章の演習で説明されています
• D. Knut、プログラミングの技術- セクション6.2.3は、AVLツリーの理論的分析に専念しています。