 学生時代から、分析的導関数を導き出し、表現を単純化するアルゴリズムに興味がありました。 このタスクは、大学の後半で関連していました。 その後、それを実装しましたが、すべてが意図した方法ではありませんでした:ILコードの代わりに、テキスト形式でC#コードを生成しただけで、アセンブリはアンロードされず、さらに分析形式で派生物を導出する方法はありませんでした しかし、関心が残ったため、そのようなライブラリを実装することにしました。 インターネット上にそのようなライブラリが多数あることは注目に値しますが、ILコードに式をコンパイルする段階、つまり 実際、コンパイルとは異なり、それほど効果的ではない解釈がどこでも実行されます。 それに、特に、自分の仕事の結果がどこかで必要になることを特に望んでいないのに、新しい技術を研究するために、私自身のためにそれを開発しました。 せっかちな人: ソースコード 、 プログラム 。
学生時代から、分析的導関数を導き出し、表現を単純化するアルゴリズムに興味がありました。 このタスクは、大学の後半で関連していました。 その後、それを実装しましたが、すべてが意図した方法ではありませんでした:ILコードの代わりに、テキスト形式でC#コードを生成しただけで、アセンブリはアンロードされず、さらに分析形式で派生物を導出する方法はありませんでした しかし、関心が残ったため、そのようなライブラリを実装することにしました。 インターネット上にそのようなライブラリが多数あることは注目に値しますが、ILコードに式をコンパイルする段階、つまり 実際、コンパイルとは異なり、それほど効果的ではない解釈がどこでも実行されます。 それに、特に、自分の仕事の結果がどこかで必要になることを特に望んでいないのに、新しい技術を研究するために、私自身のためにそれを開発しました。 せっかちな人: ソースコード 、 プログラム 。
使用済みのプログラムとライブラリ
- GOLD Parsing System-文法を記述し、さまざまな言語(C、C#、Java、JavaScript、Objective-C、Perl、Python、Rubyなど)のレクサーとパーサーのコードを生成するIDE。 LALR解析に基づいています。
- Visual Studio 2010
- GOLD.Engine-生成されたテーブルと対話するために接続された.NETのアセンブリ。
- NUnit-.NET用のオープンソースの単体テスト環境。
- ILSpy-.NET用のオープンソース逆アセンブラー 。
プロセス全体を壊した段階:
式ツリーの構築
GANTパーサージェネレーターを選択しました。ANTLRの経験があり、新しいものが欲しかったからです。 まあ、その利点は、他と比較して、この表で見ることができます 。 ご覧のとおり、ANTLRと比較すると、GOLDはLLではなくLALRアルゴリズムに基づいています。 これは、理論的には、生成されたパーサーはより高速で強力ですが、一方でデバッグできないことを意味します(GOLDでは、ファイルはバイナリ形式でダウンロードされます)。可能であれば、完全に不明瞭で不便です。 もう1つの大きな違いは、文法形式: EBNFではなくBNFです。 これは、この形式で書かれた文法は、山括弧、定義の記号、条件付きの出現と繰り返しの欠如のためにわずかに大きいサイズを持つことを意味します ( wikiにあります 。また、例えば、EBNFのようなルール
ExpressionList = Expression { ',' Expression }
次の形式で書き換えられます。
<ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression>
したがって、数式の最終的な文法は次の形式になります。
数式の文法
"Name" = 'Mathematics expressions' "Author" = 'Ivan Kochurkin' "Version" = '1.0' "About" = '' "Case Sensitive" = False "Start Symbol" = <Statements> Id = {Letter}{AlphaNumeric}* Number1 = {Digit}+('.'{Digit}*('('{Digit}*')')?)? Number2 = '.'{Digit}*('('{Digit}*')')? AddLiteral = '+' | '-' MultLiteral = '*' | '/' <Statements> ::= <Statements> <Devider> <Statement> | <Statements> <Devider> | <Statement> <Devider> ::= ';' | '.' <Statement> ::= <Expression> '=' <Expression> | <Expression> <Expression> ::= <FuncDef> | <Addition> <FuncDef> ::= Id '(' <ExpressionList> ')' | Id '' '(' <ExpressionList> ')' | Id '(' <ExpressionList> ')' '' <ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression> <Addition> ::= <Addition> AddLiteral <Multiplication> | <Addition> AddLiteral <FuncDef> | <FuncDef> AddLiteral <Multiplication> | <FuncDef> AddLiteral <FuncDef> | <Multiplication> <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation> | <Multiplication> MultLiteral <FuncDef> | <FuncDef> MultLiteral <Exponentiation> | <FuncDef> MultLiteral <FuncDef> | <Exponentiation> <Exponentiation> ::= <Exponentiation> '^' <Negation> | <Exponentiation> '^' <FuncDef> | <FuncDef> '^' <Negation> | <FuncDef> '^' <FuncDef> | <Negation> <Negation> ::= AddLiteral <Value> | AddLiteral <FuncDef> | <Value> <Value> ::= Id | Number1 | Number2 | '(' <Expression> ')' | '|' <Expression> '|' | '(' <Expression> ')' '' | '|' <Expression> '|' '' | Id ''
トークンを除いて、文法ではすべてが明らかなようです: Number1 = {Digit} +( '。' {Digit} *( '(' {Digit} * ')')?)? この設計により、次の形式の行を解析できます。0.1234(56)。これは、合理的な小数部を意味する:61111/495000 このような文字列を分数に変換する方法については、後で説明します。
したがって、コンパイル済みの文法テーブル(コンパイル済み文法テーブルファイル)が生成され、パーサークラスフレームワークが作成された後、適切なASTツリーを構築するために後者を変更する必要があります。 この場合のパーサークラスフレームワークは、すべての文法ルールのループ、トークンの不正なシーケンスやその他のエラーの場合の例外処理を含む.csファイルです(ちなみに、GOLDにはこのようなフレームワークの異なるジェネレーターがあり、Cook .NETを選択しました) したがって、この場合、「適切な」とは、次のタイプを持つことができるノードで構成されるツリーを意味します。
- 計算済み -コンパイラーが受け入れ可能な二重形式で計算された定数を表すノード。たとえば、「0.714285714285714」、「0.12222222222222222」。 それらが同じであっても、そのような定数ごとに新しいオブジェクトが作成されます。
- 値 -計算された定数を有理数の形式で表すノード、つまり 1は「1/1」、「0.1(2)」は「11/90」、「0.1234」は「617/5000」として表されます。 それらが同じであっても、そのような定数ごとに新しいオブジェクトが作成されます。
- 定数 -未定義の定数を表すノード、たとえば「a」、「b」など。2つの定数が式で見つかった場合、それらは1つのノードを指します。
- 変数 - 変数を表すノード、たとえば「x」、「y」など。特定の変数が式で複数回出現する場合、その変数と未定義の定数に対して1つのオブジェクトのみが作成されます。 定数と変数の区別は、分析導関数の導出の段階でのみ重要であり、他の場合、この知識は必要ないことを理解することが重要です。
- 関数 - 関数を表すノード、たとえば、「+」、「sin」、「^」など。 子を持つことができる唯一のノード。
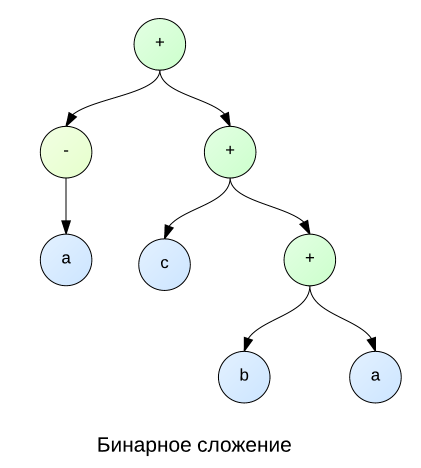
図には、すべてのタイプのノードが明確に示されています。

文法から、結果のツリーのノードには子(値や変数など)がないか、標準関数(cos、加算、べき乗など)の場合は1〜2個の子があることがわかります。 他のすべての関数にはさらに引数がありますが、考慮されませんでした。
したがって、すべてのノード(または機能を持つノード)には、0〜2個の子が含まれます。 これは理論的な観点から当てはまります。 しかし、実際には、「+」および「*」関数の子の数を無制限にし、後で検討する単純化のタスクを容易にする必要がありました。 ちなみに、「-」や「/」などのバイナリ演算も同じ理由で破棄する必要がありました(右側の否定による加算と右側の反転による乗算に置き換えられました)。
そのため、解析段階で、各ルールのすべてのノードが落ちるか、 Nodesというバッファーから取得されます。 したがって、プロセス全体の最後に、右側と左側の部分を持つ1つ以上の関数がこのバッファーに残ります。 また、構文解析の過程で、加算関数と乗算関数が多国語ですぐに作成されるように、関数の現在の引数の数と現在の関数の型をそれぞれ格納する追加のバッファーArgsCountとArgsFuncTypesが使用されました。 したがって、たとえば、乗算関数の場合、次のコードが使用されます。
最初の乗数の処理:
// <Multiplication> ::= <Exponentiation> if (MultiplicationMultiChilds) PushFunc(KnownMathFunctionType.Mult);
i番目の乗数の処理:
// <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation> // <Multiplication> ::= <Multiplication> MultLiteral <FuncDef> if (KnownMathFunction.BinaryNamesFuncs[r[1].Data.ToString()] == KnownMathFunctionType.Div) Nodes.Push(new FuncNode(KnownMathFunctionType.Exp, new MathFuncNode[] { Nodes.Pop(), new ValueNode(-1) })); ArgsCount[ArgsCount.Count - 1]++;
最後の乗数の処理:
// <Addition> ::= <Multiplication> if (MultiplicationMultiChilds) PushOrRemoveFunc(KnownMathFunctionType.Mult); if (AdditionMultiChilds) PushFunc(KnownMathFunctionType.Add);
このコードは、たとえば、乗算がない場合、 PushOrRemoveFuncを使用して要素がゼロの最後の乗算関数を削除する必要があることを示しています。 追加するには、同様のアクションを実行する必要があります。
単一の引数の関数、バイナリ関数、定数、変数、値の処理は簡単であり、 MathExprParser.csでこれらすべてを確認できます。
分析導関数の計算
この段階で、関数をその導関数に変換する必要があります。
最初の段階からわかるように、作成された式ツリーには4つのタイプのノードしかありません(5番目のノードは後で表示されます)。 それらについて、導関数を定義します。
- 値 '= 0
- 定数 '= 0
- 変数 '= 1
- 関数 '=誘導体[関数]
説明してみましょう:導関数については、事前に準備された表形式の値を取得する必要があり、この値には導関数があるため、特定の困難が生じます。 プロセスは本質的に再帰的です。 このような実装された置換の完全なリストは、以下のネタバレの下にあります。
デリバティブのリスト
(f(x) ^ g(x))' = f(x) ^ g(x) * (f(x)' * g(x) / f(x) + g(x)' * ln(f(x)));"); neg(f(x))' = neg(f(x)');"); sin(f(x))' = cos(f(x)) * f(x)'; cos(f(x))' = -sin(f(x)) * f(x)'; tan(f(x))' = f(x)' / cos(f(x)) ^ 2; cot(f(x))' = -f(x)' / sin(f(x)) ^ 2; arcsin(f(x))' = f(x)' / sqrt(1 - f(x) ^ 2); arccos(f(x))' = -f(x)' / sqrt(1 - f(x) ^ 2); arctan(f(x))' = f(x)' / (1 + f(x) ^ 2); arccot(f(x))' = -f(x)' / (1 + f(x) ^ 2); sinh(f(x))' = f(x)' * cosh(x); cosh(f(x))' = f(x)' * sinh(x); arcsinh(f(x))' = f(x)' / sqrt(f(x) ^ 2 + 1); arcosh(f(x))' = f(x)' / sqrt(f(x) ^ 2 - 1); ln(f(x))' = f(x)' / f(x); log(f(x), g(x))' = g'(x)/(g(x)*ln(f(x))) - (f'(x)*ln(g(x)))/(f(x)*ln(f(x))^2);
すべての派生物がコード内でハードに記述されているわけではなく、動的に入力および解析することもできます。
上記のように、これらはいくつかの引数を持つ関数であるため、このリストには加算または乗算はありません。 そして、そのようなルールを解析するには、多くのコードを書く必要があります。 同じ理由で、機能の構成はありません。 (f(g(x))) '= f(g(x))' * g(x) 'の代わりに、すべての関数は関数の構成として表されます。
また、Derivativesの関数(つまり、未定義の関数)の置換が見つからなかった場合、それは単にストロークのある関数に置き換えられます。 f(x)はf(x) 'になります。
分析導関数が正常に取得された後、結果の式には、a + 0、a * 1、a * a ^ -1など、多くの「ガベージ」があるという問題が発生します。また、結果の式はより最適な方法で計算できます。 たとえば、単純な式であっても、見苦しい式になります。
(x^2 + 2)' = 0 + 2 * 1 * x ^ 1
単純化は、このような欠点に対処するために使用されます。
式の簡略化
この段階では、導関数を計算する段階とは異なり、単純な規則を別の場所に書き留めませんでした。加算と乗算の関数はいくつかの引数の関数であるため、そのような規則を作成するのはある程度困難です反復言語のコンテキスト。
トピックの冒頭で、加算と乗算がn項関数として表される理由のトピックに触れました。 下の写真に示されている状況を想像してください。 ここで、aと-aが省略されていることがわかります。 しかし、バイナリ関数の場合にこれを行う方法は? これを行うには、ノードa 、 b、およびcを反復処理して、 aおよび-aが同じノードの子であることを後で発見します。これは、ノードとともにノードを削減できることを意味します。 ただし、右の図に示すように、ツリーをソートすることは、単純なタスクではありません。すべての子を一度にすべてのアクションを一度に実行する方がはるかに簡単だからです。 ところで、このような列挙型により、 結合性と可換性の数学的特性を作成できます。
 |  |
単純化プロセス中に、2つのノードを比較するという問題が発生します。2つのノードは、4つのタイプのいずれかになります。 これは、たとえば、sin(x + y)や-sin(x + y)などの式を減らすために必要です。 ノードごとにノード自体とそのすべての子孫を比較できることは明らかです。 しかし、問題は、この方法では、たとえばsin(x + y)や-sin(y + x)のように、用語や因子が再配置される状況に対処できないことです。 この問題を解決するために、可換性の特性が満たされる用語または因子の予備的なソートが使用されます(つまり、加算と減算)。 ノードは、次の図に示すように比較されます。 値は定数より小さい、定数は変数より小さい、など。 関数の場合、名前だけでなく引数の数と引数自体も比較する必要があるため、すべてが少し複雑になります。

したがって、上記のすべての変換と列挙の後、元の式は非常に単純化されます。
合理的な分数処理
私が見つけた合理的な実装では、通常の文字列型、たとえば0.666666は、特定の分子と分母を持つ分数型に変換されませんでした。 一定の精度で2/3で。 次に、多くのオプションを使用して実装を作成することにしました。 以下の関数は、たとえば、特定の数が純粋に非合理的であるか、それが周期または有限小数部を持ち、合理的なもの、たとえば一定の精度でsin(pi)から0に変換できるかを決定できます。 一般的に、 stackoverflow.comへの私の回答のその他の詳細を参照してください。 メソッドの簡単なグラフィカルな説明を下の図に示し、コードを下のリストに示します。 それにもかかわらず、標準的な数学関数とdouble型の精度は、有理数と実数の通常の認識には十分ではありませんが、理論的にはすべてが機能することに注意してください。
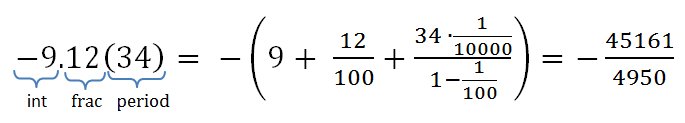
小数を小数に変換
/// <summary> /// Convert decimal to fraction /// </summary> /// <param name="value">decimal value to convert</param> /// <param name="result">result fraction if conversation is succsess</param> /// <param name="decimalPlaces">precision of considereation frac part of value</param> /// <param name="trimZeroes">trim zeroes on the right part of the value or not</param> /// <param name="minPeriodRepeat">minimum period repeating</param> /// <param name="digitsForReal">precision for determination value to real if period has not been founded</param> /// <returns></returns> public static bool FromDecimal(decimal value, out Rational<T> result, int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9) { var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture); var strs = valueStr.Split('.'); long intPart = long.Parse(strs[0]); string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' }); string fracPart; if (trimZeroes) { fracPart = fracPartTrimEnd; decimalPlaces = Math.Min(decimalPlaces, fracPart.Length); } else fracPart = strs[1]; result = new Rational<T>(); try { string periodPart; bool periodFound = false; int i; for (i = 0; i < fracPart.Length; i++) { if (fracPart[i] == '0' && i != 0) continue; for (int j = i + 1; j < fracPart.Length; j++) { periodPart = fracPart.Substring(i, j - i); periodFound = true; decimal periodRepeat = 1; decimal periodStep = 1.0m / periodPart.Length; var upperBound = Math.Min(fracPart.Length, decimalPlaces); int k; for (k = i + periodPart.Length; k < upperBound; k += 1) { if (periodPart[(k - i) % periodPart.Length] != fracPart[k]) { periodFound = false; break; } periodRepeat += periodStep; } if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5') { var ind = (k - i) % periodPart.Length; var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k); ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1; ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length)); if (periodTailPlusOne == fracTail) periodFound = true; } if (periodFound && periodRepeat >= minPeriodRepeat) { result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart); break; } else periodFound = false; } if (periodFound) break; } if (!periodFound) { if (fracPartTrimEnd.Length >= digitsForReal) return false; else { result = new Rational<T>(long.Parse(strs[0]), 1, false); if (fracPartTrimEnd.Length != 0) result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length)); return true; } } return true; } catch { return false; } } public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart) { Rational<T> firstFracPart; if (fracPart != null && fracPart.Length != 0) { ulong denominator = TenInPower(fracPart.Length); firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator); } else firstFracPart = new Rational<T>(0, 1, false); Rational<T> secondFracPart; if (periodPart != null && periodPart.Length != 0) secondFracPart = new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) * new Rational<T>(1, Nines((ulong)periodPart.Length), false); else secondFracPart = new Rational<T>(0, 1, false); var result = firstFracPart + secondFracPart; if (intPart != null && intPart.Length != 0) { long intPartLong = long.Parse(intPart); result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result; } return result; } private static ulong TenInPower(int power) { ulong result = 1; for (int l = 0; l < power; l++) result *= 10; return result; } private static decimal TenInNegPower(int power) { decimal result = 1; for (int l = 0; l > power; l--) result /= 10.0m; return result; } private static ulong Nines(ulong power) { ulong result = 9; if (power >= 0) for (ulong l = 0; l < power - 1; l++) result = result * 10 + 9; return result; }
式のコンパイル
単純化段階の後、結果のセマンティックツリーをILコードに変換するために、Mono.Cecilを使用しました。
プロセスの開始時に、コマンドが記述されるアセンブリ、クラス、およびメソッドが作成されます。 次に、各FuncNodeについて、プログラムに表示される回数が計算されます。 たとえば、関数sin(x ^ 2)* cos(x ^ 2)がある場合、その中にxを2のべき乗する関数が2回発生し、関数sinとcosが一度に1つずつ発生します。 将来、関数計算の繰り返しに関するこの情報は、次のように使用されます(つまり、この方法では、2番目の関数は同じ関数を2回計算しません)。
if (!func.Calculated) { EmitFunc(funcNode); func.Calculated = true; } else IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
このすべてのコードを生成した後、下の図に示すように、ILコードの他の最適化が可能です。
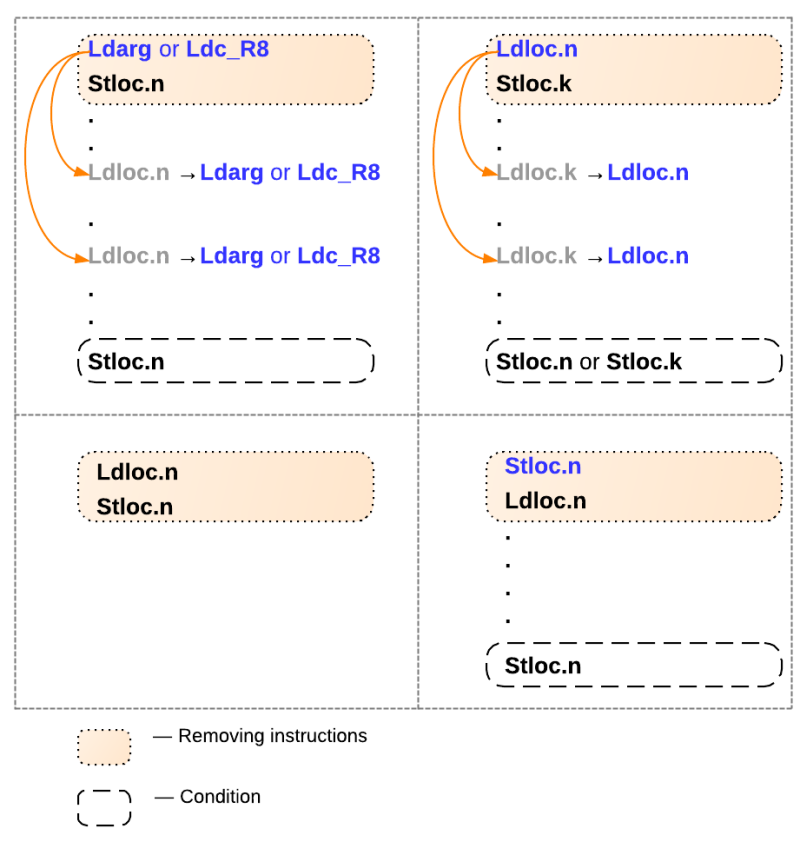
この写真では:
- Ldarg-特定の関数引数をスタックにロードする操作。
- Ldc_R8-特定のdouble値をスタックにロードします。
- Stloc.n-スタックから最後の値を取得し、ローカル変数nに保存します。
- Ldloc.n-ローカル変数n をスタックにプッシュします。
特定の条件が満たされた場合、ベージュ色のボックス内の指示を削除できます。 たとえば、左上の画像の場合は次のように説明されます:現在の命令が関数から引数を読み込んでいるか、定数を読み込んでおり、次の命令がそれをローカル変数nに保存している場合、ローカル変数nの読み込み命令を読み込みで置き換えることにより、この命令のブロックを削除できます関数の引数または定数の読み込み。 ローカル変数nの最初のsaveステートメントまで置換プロセスを続けます。 他の3つのケースも同様に説明されています。 たとえば、シーケンスLdloc.n ; Stloc.nはすぐに削除できます。
これらの最適化は、コードに分岐がない場合にも適用できることに注意する価値があります。これは明らかです(完全に明らかでない場合は、考えてみることをお勧めします)。 しかし、私の場合、数学関数とその導関数のコードにはサイクルを含めることができないため、これはすべて機能します。
高速べき乗
私は、ほとんど誰もが、力を素早く力に上げるためのアルゴリズムについて知っていると思います。 ただし、以下のアルゴリズムはコンパイルレベルで表示されます。
ILコードに実装された高速べき乗アルゴリズム
if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); }
高速累乗アルゴリズムは最適な累乗アルゴリズムではないことに注意してください。 たとえば、次の2つの方法で同じ変数を5回乗算します。 x ^ 4 + x ^ 3 + x ^ 2 + x = x *(x *(x *(x + 1)+ 1)+ 1)などの最適化も実装されていません。
- var t = a ^ 2; a * a * a * a * a * a * a = t ^ 2 * t-通常の「高速」アルゴリズム。
- a * a * a * a * a * a * a =(a ^ 3)^ 2-最適な「高速」アルゴリズム。
ところで、通常の固定数doubleの場合、上記の乗算の異なる順序での乗算の結果は異なることに注意してください(つまり(a ^ 2)^ 2 * a ^ 2!=(A ^ 3)^ 2 ) このため、一部のコンパイラはこれらの式の多くを最適化しません。 stackoverlofwにはこれに関する興味深いQ&Aがあります。 なぜGCCはa * a * a * a * a * aを(a * a * a)*(a * a * a)に最適化しないのですか? そして、 なぜMath.Pow(x、2)はx * xコンパイラーにもJITにも最適化されていないのですか 。
ローカル変数の最適化
前の手順からわかるように、ローカル変数は、元の式で複数回発生するすべての関数の結果を格納するために使用されます。 ローカル変数を操作するには、2つの単純な命令stlocとldlocのみが使用されます。これらは、このローカル変数の数を担当する1つの引数を使用します。 ただし、ローカル変数の数が、計算結果が繰り返し表示されるたびに(作成するために)インクリメントされる場合、ローカル変数が多数存在する可能性があります。 この問題を軽減するために、ローカル変数のライフサイクルを圧縮するアルゴリズムが実装されました。そのプロセスは下の図に明確に示されています。 ご覧のとおり、式では5つのローカル変数の代わりに3つしか使用できません。ただし、この「貪欲な」アルゴリズムは最適な順列ではありませんが、実装するタスクには非常に適しています。
 |  |
未定義の関数とその派生物のコンパイル
開発したライブラリでは、f(x)という形式の1つの変数の単純な関数だけでなく、f(x、a、b(x))などの他の変数も使用できます。ここで、aは未知の定数で、b(x)は未知の関数ですデリゲートとして送信されます。 ご存知のように、関数の導関数の定義は次のとおりです:b(x) '=(b(x + dx)-b(x))/ dx。 , :
ldarg.1 ldarg.0 callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) ret
(dx = 0.000001)
ldarg.1 ldarg.0 ldc.r8 1E-06 add callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) ldarg.1 ldarg.0 callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) sub ldc.r8 0.000001 div ret
, , .
テスト中
, MathFunction.Tests. WolframAlpha.NET .
WolframAlpha
WolframAlpha.NET — API wolframalpha . , , , , . :
public static bool CheckDerivative(string expression, string derivative) { return CheckEquality("diff(" + expression + ")", derivative); } public static bool CheckEquality(string expression1, string expression2) { WolframAlpha wolfram = new WolframAlpha(ConfigurationManager.AppSettings["WolframAlphaAppId"]); string query = "(" + expression1.Replace(" ", "") + ")-(" + expression2.Replace(" ", "") + ")"; QueryResult result = wolfram.Query(query); result.RecalculateResults(); try { double d; return double.TryParse(result.GetPrimaryPod().SubPods[0].Plaintext, out d) && d == 0.0; } catch { return false; } }
, , (MethodInfo):
Domain = AppDomain.CreateDomain("MathFuncDomain"); MathFuncObj = _domain.CreateInstanceFromAndUnwrap(FileName, NamespaceName + "." + ClassName); Type mathFuncObjType = _mathFuncObj.GetType(); Func = mathFuncObjType.GetMethod(FuncName); FuncDerivative = mathFuncObjType.GetMethod(FuncDerivativeName);
:
return (double)Func.Invoke(_mathFuncObj, new object[] { x })
:
if (_domain != null) AppDomain.Unload(Domain); File.Delete(FileName);
IL
IL , , C# csc.exe Release ,
x ^ 3 + sin(3 * ln(x * 1)) + x ^ ln(2 * sin(3 * ln(x))) - 2 * x ^ 3
| csc.exe .NET 4.5.1 | MathExpressions.NET |
|
|
, C# ILSpy , , .. に
(ln(2 * sin(3 * ln(x))) * x ^ -1 + 3 * ln(x) * cos(3 * ln(x)) * sin(3 * ln(x)) ^ -1 * x ^ -1) * x ^ ln(2 * sin(3 * ln(x))) + 3 * cos(3 * ln(x)) * x ^ -1 + -(3 * x ^ 2)
double arg_24_0 = 2.0; double arg_1A_0 = 3.0; double num = Math.Log(x); double num2 = arg_1A_0 * num; double num3 = Math.Sin(num2); double num4 = Math.Log(arg_24_0 * num3); double arg_3B_0 = num4; double num5 = 1.0 / x; double arg_54_0 = arg_3B_0 * num5; double arg_4F_0 = 3.0 * num; num = Math.Cos(num2); return (arg_54_0 + arg_4F_0 * num / num3 * num5) * Math.Pow(x, num4) + num * num5 * 3.0 - x * x * 3.0;
, . , , , double arg_24_0 = 2.0; , .
, , , , , .
おわりに
C#, , , - . , , OpenSource maxima lisp. , F# codeproject , , . , , , .
Github: source . : MathExpressions.NET . . - .
PS , . .
UPDATE: , , . , . .