👨🏾 ♒️ 👩🏼‍🎤 高速モジュロインデックス乗算 👨‍👩‍👧 🍛 🌜

はじめに

通常、この資料には豊富な数式が用意されており、数学者向けに設計されています。ハードウェアレベルでマイクロエレクトロニクスにこの方法を適用するという観点から、単純な数値例を使用して最もアクセスしやすいものにしようとします。数値の例では、明確にするためにp = 11が使用されます。

問題の声明

次の形式の乗算を実行する必要があるとします： res = (a*b) mod p

、ここで

0 <= a < p

0 <= b < p

p

は素数です。

mod p

剰余をモジュロで求める演算。

そして、乗算操作や除算の残りをそのままとる操作がない低レベルで実行する必要があります。そうでない場合は、非常に困難です（たとえば、電子デバイスで）。

最も簡単な解決方法

最初に頭に浮かぶのは、乗算してから除算して残りを取得することです。このアプローチには存在する権利がありますが、操作の数の点で非常にコストがかかり、実装が非常に困難です。
2番目に考えられることは、サイズp

2次元乗算テーブルを使用してこの演算を実装することです。 p

小さい場合は理にかなっていますが、pが増加すると、テーブルを格納するコストが2次的に増加します（図1）。

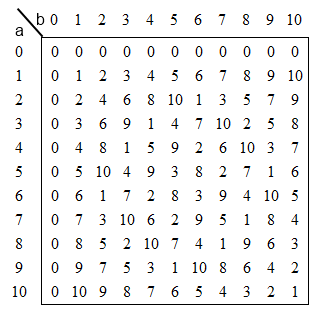
図1. p = 11のpを法とする乗算表

インデックスメソッドの乗数

ただし、次元p

1つの（または2つの便宜のために）テーブルを必要とするメソッドがあります。この方法は、乗算を加算で置き換えることに基づいています。また、次の図（図2）で概略的に説明できます。

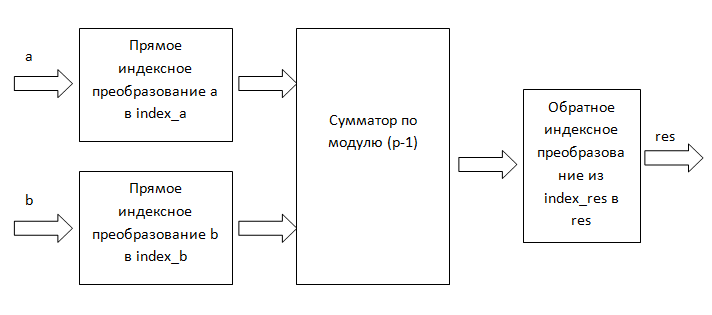
図2.インデックスの乗算。

これが可能な理由を説明しましょう。数値のインデックス表現は、 p

法とする逆微分根の概念に基づいています[1]。原始根wは整数であり、その累乗0, 1, 2, …, (p-2)

はp

法とする非反復剰余を与えます。素数根は常に任意の素数p

存在します（1801年にガウスによって証明されました）。この場合、区間(0; p)

各整数q

は、 q = (w

ⁱ ) mod p

ような数値i

関連付けることができます。したがって、次の通信を取得します。

(a*b) mod p <-> w^((ia+ib) mod (p-1))

[2]。

モジュールp = 11

例を考えてみましょう。このモジュラス値のプリミティブルートw

は2ですw

を0、1、... 9の累乗にすると、一意の結果が得られることを簡単に確認できます。

（2 ⁰ ） mod

11 = 1 mod

11 = 1
（2 ¹ ） mod

11 = 2 mod

11 = 2
（2 ² ） mod

11 = 4 mod

11 = 4
（2 ³ ） mod

11 = 8 mod

11 = 8
（2 ⁴ ） mod

11 = 16 mod

11 = 5
（2 ⁵ ） mod

11 = 32 mod

11 = 10
（2 ⁶ ） mod

11 = 64 mod

11 = 9
（2 ⁷ ） mod

11 = 128 mod

11 = 7
（2 ⁸ ） mod

11 = 256 mod

11 = 3
（2 ⁹ ） mod

11 = 512 mod

11 = 6

通常の{q}

{i}

表現とインデックス{i}

表現間の変換テーブルを取得するには、結果の値のペアを昇順で並べ替える必要があります。したがって、モジュールp

= 11の直接変換テーブルは次のようになります。

q	1	2	3	4	5	6	7	8	9	10
私は	0	1	8	2	4	9	7	3	6	5

また、 p

= 11モジュールの逆変換テーブルは次のようになります。

私は	0	1	2	3	4	5	6	7	8	9
q	1	2	4	8	5	10	9	7	3	6

式（3 * 5） mod

11の値を見つけます。数字3と5には、対応するインデックス8と4があります（表1を参照）。これらのインデックスをモジュロ（11-1）= 10で合計すると、結果（8 + 4） mod

10 = 12 mod

10 = 2が得られます。表2から、インデックス2の逆変換により4に等しい最終結果が得られます。

考慮された例のm = 11を法とするインデックス乗数の構造図を次の図に示します（図3）。

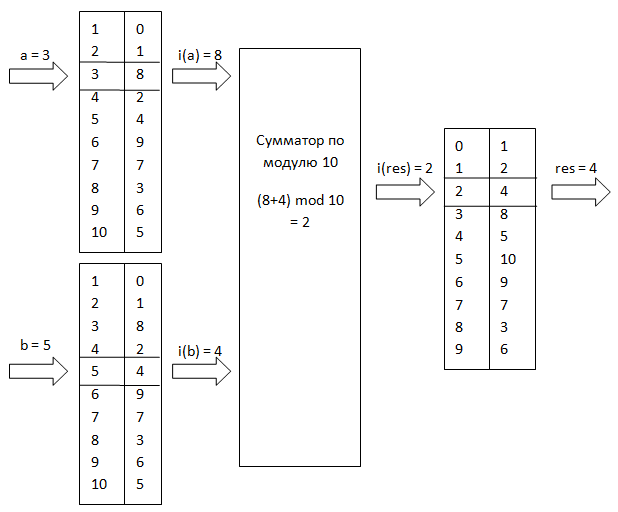
図3. p = 11のインデックス乗数のスキーム

入力のゼロ値

テーブルをよく見ると、入力データにゼロ値がないことがわかります。これは、 i

の値がない場合にw

ⁱ ！= 0であるという事実によるものです。このケースは個別に処理されます（または、処理の特別なルールを持つ特異点の概念が導入されます）。乗数の入力の1つに0が表示される場合、出力にも0があります。これは、乗算の規則から直接に従います。

乗算器の並列化

乗算をさらに高速に実行できることがわかりました。数(p-1)

を相互に単純な因子p-1 = m1*m2*…*mr

に分割できる場合、加算演算はより小さな次元のr

加算演算に分割できます。この場合、インデックスは次の式に従って長さr

ベクトルに変換されます：（ i mod m1, i mod m2, …, i mod mr

）。そして、加算はベクトルの各要素に対して独立して実行されます。

これを例として考えてください。 p

= 11の場合、 p

-1 = 10の値であり、相互に単純な要因に一意に分割できます：10 = 2 * 5（ m1

= 2、 m2

= 5）。この場合、表1は次のように記述できます。

q	1	2	3	4	5	6	7	8	9	10
私は	0	1	8	2	4	9	7	3	6	5
（i `mod` 2、i `mod` 5）	（0、0）	（1、1）	（0、3）	（0、2）	（0、4）	（1、4）	（1、2）	（1、3）	（0、1）	（1、0）

それぞれ次のような逆変換の表：

（i `mod` 2、i `mod` 5）	（0、0）	（0、1）	（0、2）	（0、3）	（0、4）	（1、0）	（1、1）	（1、2）	（1、3）	（1、4）
q	1	9	4	3	5	10	2	7	8	6

前の例のように、値（3 * 5） mod

11を見つけます。まず、テーブルで対応するベクトルを探します：3->（0、3）、5->（0、4）。次に、要素ごとに要素を追加します（（0 + 0） mod

2、（3 + 4） mod

5）=（0、2）。逆変換の表から答えを見つけます：（0、2）-> 4.並列乗算スキームを以下に示します（図4）：

図4. p = 11の並列インデックス乗数のスキーム

プリミティブルートを探す方法は？

正直に言うと、私はこの質問をしませんでした。 2からpまでの徹底的な検索を使用します。または、既製のシーケンスoeis.org/A046145を使用できます。より効率的な方法がある場合は、コメントを書いてください。

加算器モジュロ（p-1）を設計する方法は？

加算器モジュロ(p-1)

の入力データの特性により、つまり、両方の入力がp-1

より小さい数を受け取るため、合計が2*(p-1)

より小さいことを意味します。このことから、標準加算器のいずれかを使用でき、その出力は次のアルゴリズムに従って調整されます：値が(p-1)

以上の場合、結果から(p-1)

減算し、そうでない場合はそのままにします。

Verilogジェネレーター

余暇には、モジュロインデックス乗数を実装するためにVerilogのオンラインジェネレーターを作成しました。そこには、彼の作品の図が描かれています。

11を法とする乗算のVerilog

モジュロ31乗算のVerilog

1000までの任意の数のVerilogジェネレーター

文学

[1] en.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B2%D0%BE%D0%BE%D0%B1%D1%80%D0%B0%D0% B7％D0％BD％D1％8B％D0％B9_％D0％BA％D0％BE％D1％80％D0％B5％D0％BD％D1％8C_％28％D1％82％D0％B5％D0％ BE％D1％80％D0％B8％D1％8F_％D1％87％D0％B8％D1％81％D0％B5％D0％BB％29

[2] www.researchgate.net/publication/224735018_A_fast_RNS_Galois_field_multiplier

著者から

記事への追加がある場合は、コメントでそれらを見て喜んでいます。それでも、誰かが投げる何かを持っている場合、記事は詳細とのリンクで貧弱であることが判明しました。 =）

高速モジュロインデックス乗算