徹底的な検索に関するアドバイスは、最初は真剣に考えなかったので、検索には非常に時間がかかることを考慮して、考えさせられました。 鉱山がフィールド全体に散在している場合、これは実際に当てはまります。 しかし、 IXBTからサッパーをダウンロードした後 、私はこれがまったく必要ないことを理解しました。 開いている番号に直接隣接するセルのみを考慮することは理にかなっています。 これらの数値は、他のセルの地雷の可能性には影響しません。
ちなみに、ダウンロードしたサッパーを調べたところ、計算時にフィールド内の残りの地雷数をまったく考慮していないことがわかりました。 一見したところ、これは重要ではありません。たとえば、単一の「4」確率の周りでは常に50/50になるからです。 ただし、この要因を無視すると、非常に悪い結果が生じる場合があります。次に例を示します。
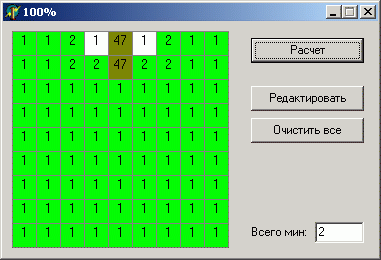
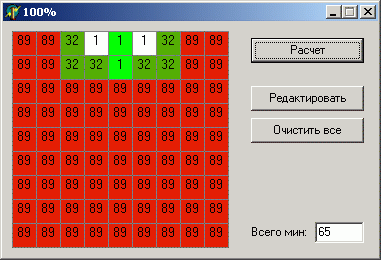
データは鉱山の数を除いてまったく同じですが、結果の違いは非常に重要です。
なぜあなたはこれが起こっているのかあなた自身が推測すると思います。 地雷の配置には2つの方法があります:ユニット間の1つの地雷(近くにない)または2つの地雷、各ユニットに1つの地雷。 フィールド全体に2つの地雷がある場合、ユニットの間に1つの地雷が配置される可能性が高くなりますが、2つ目の地雷はフィールドのほぼすべてのセルに配置できます。 逆に、地雷が多い場合、6セル(ユニットの隣)の領域に地雷がなくなる可能性は低くなります。
IXBTからの計算:
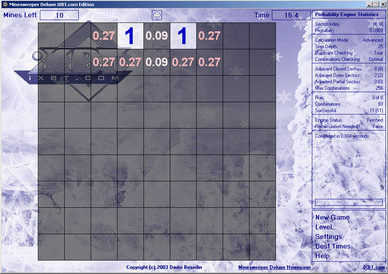
鉱山の数に関係なく、確率は同じです。 彼のデータに基づいて、私はオプションを列挙するとき、彼はそれらがすべて同等にありそうであると暗示しているという結論に達しましたが、例からわかるように、これは完全にそうではありません。
各ケースの確率を計算することで、少し面倒なことが起こりました。 列挙の過程でバリアントが条件を満たした場合、このケースの確率を計算し、取得した数を地雷があるすべてのセルに追加する必要がありました(現在のバージョンでのみ取得された仮想地雷)。 計算自体は難しくありませんが、組み合わせの基本のみが使用されます。
すべてが完全に整理され、得られた確率は理論計算とプログラムの最初のバージョンによって完全に確認されたため、この良いメモで終了することは素晴らしいことです。 しかし、これは、公開番号に隣接するセルの数がそれほど多くない場合です。 数が23を超えると、計算に1秒以上かかりましたが、あまり快適ではありませんでした。 そのため、実証済みの方法が採用されました(前のトピックで説明したモンテカルロ)。 同じ隣接セルでランダムセットが生成されるため、反復回数を1万から100万に増やすことができます。 残念ながら、困難な場合にはエラーが引き続き発生しますが、これは非常にまれです。 しかし、一般的には正確かつ迅速に動作します。 こちらからダウンロードできます。
主な目標。
プログラムの準備ができたとき、鉱山の数から勝ちの頻度をチェックすることは興味深いものになりました。 ゲームは、複雑さと時間に応じて、千から百万まで開催されました。 図には1から32までの数字しか示されていないため、確率は非常に小さくなります。 残りは以下です。
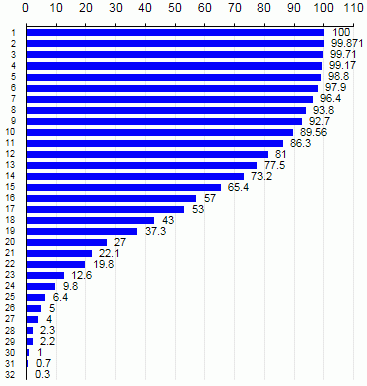
35: 17 ( 10 ) 0.17%
40: 10 ( 100 ) 0.01%
45: 3 ( 100 ) 0.003%
50: 6 ( ) 0.0006%
60: 2 ( ) 0.0002%
70: 0 ( ) ?
75: 6 ( ) 0.0006%
76: 32 ( ) 0.0032%
77: 183 ( ) 0.0183%
78: 1552 ( ) 0.1552%
79: 25350 ( ) 2.535%
ご覧のとおり、関数は非常にスムーズです。 私はそのための実験式を見つけようとしましたが、これまでのところ役に立ちませんでした。
特に、64個の鉱山で追い抜くことができるかどうかを尋ねられたM_orgについては 、1000万回運転しましたが、勝ちませんでした。 しかし今では、79回目でも弱いわけではないと安全に答えることができます:)