メモリの速度と頻度-これが主な理由であり、これにより「無料のケーキ」が得られます(リンク)。 そのため、メモリをできる限り効率的に使用することが重要であり、さらにキャッシュと同じくらい高速に使用することが重要です。 特定のコンピューター用にプログラムを最適化するには、プロセッサーキャッシュの特性(レベル数、サイズ、行の長さ)を知っておくと便利です。 これは、システムカーネル、数学ライブラリなどの高性能コードで特に重要です。
キャッシュの特性を自動的に決定する方法は? (もちろん、他のOSで簡単に実装できるアルゴリズムを取得したいという理由だけでcpuinfoが解析されているとは見なされません。それは便利ですよね?)
理論のビット
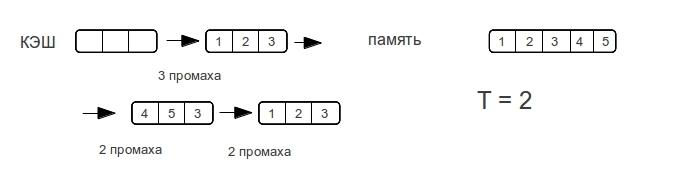
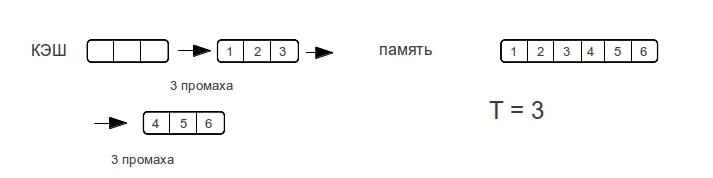
現在、広く使用されているキャッシュには、ダイレクトマッピングキャッシュ、アソシエイティブキャッシュ、マルチアソシエイティブキャッシュの3種類があります。
直接マッピングキャッシュ
-このRAMの行は、キャッシュの1行に表示できますが、キャッシュの各行には、RAMの多くの可能な行を表示できます。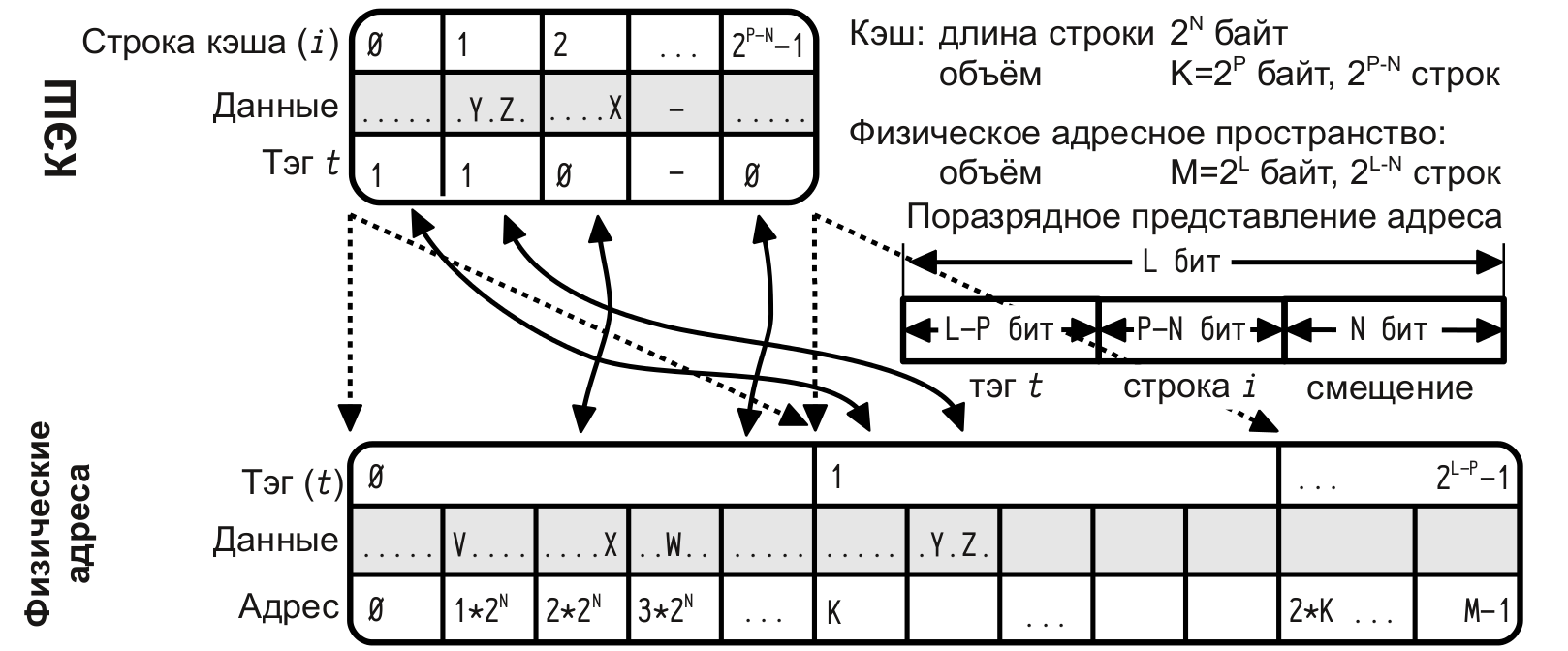
連想キャッシュ
-RAMの任意の行をキャッシュの任意の行にマップできます。
複数の連想キャッシュ
-キャッシュメモリはいくつかの「バンク」に分割され、各バンクはダイレクトマッピングを備えたキャッシュとして機能するため、RAMラインは、(ダイレクトマッピングの場合のように)可能なキャッシュエントリだけでなく、いくつかのバンクの1つで表示できます。 ; バンクは、キャッシュ内の各ラインのLRUまたはその他のメカニズムに基づいて選択されます。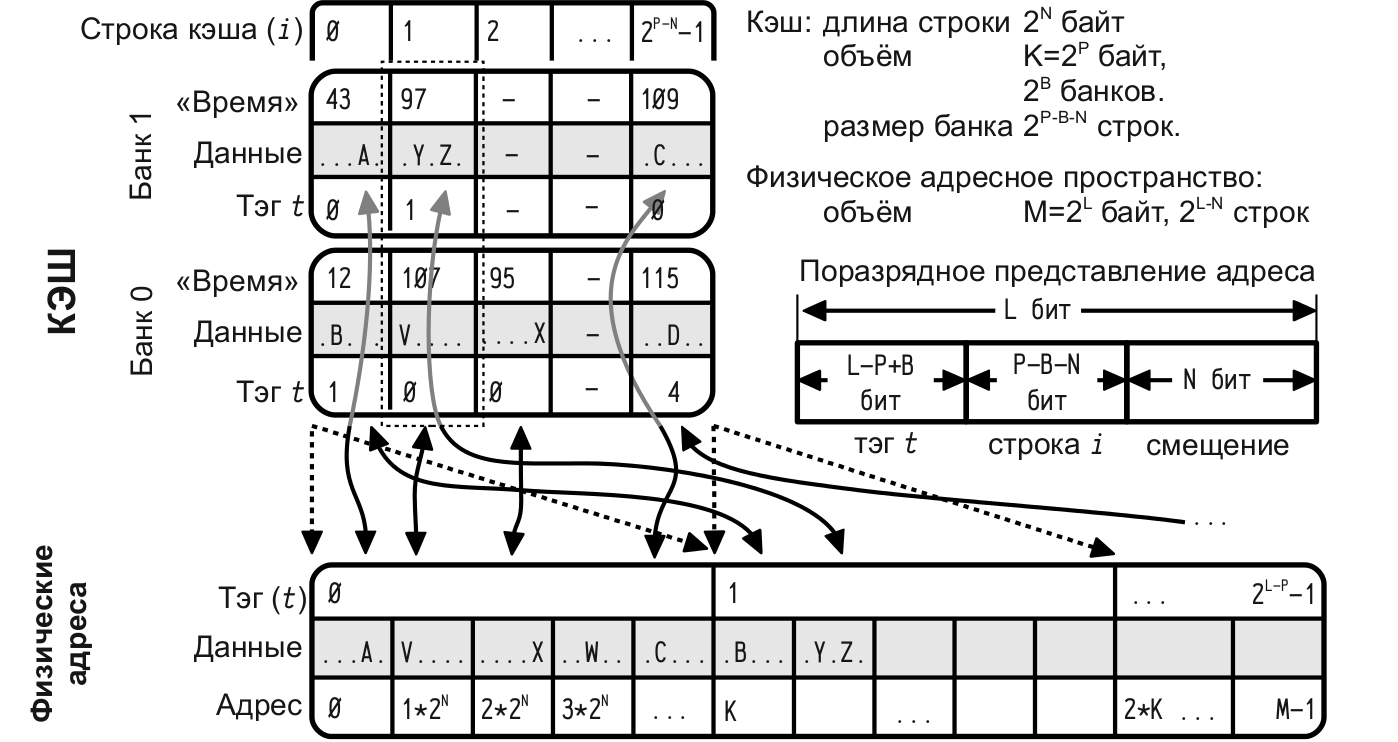
LRU-「最長未使用」ライン、メモリキャッシュの混雑。
アイデア
キャッシュレベルの数を決定するには、メモリアクセスの順序を考慮する必要があります。この順序で、遷移が明確に表示されます。 キャッシュレベルが異なると、主にメモリの応答速度が異なります。 キャッシュミスの場合、L1キャッシュは次のメモリレベルでデータを検索し、データサイズがL1より大きくL2より小さい場合、メモリ応答速度はL2応答速度になります。 上記の説明は、一般的な場合にも当てはまります。
ミスキャッシュを明確に確認し、さまざまなデータサイズでテストするテストを選択する必要があることは明らかです。
LRUアルゴリズムに従って動作するマルチアソシエイティブキャッシュのロジックを知っていれば、キャッシュが「落ちる」アルゴリズムを見つけるのは難しくありません。 効率基準は、1回のメモリアクセスの時間です。 当然、文字列のすべての要素に一貫して適用し、繰り返して結果を平均する必要があります。 たとえば、ラインがキャッシュに収まる場合もありますが、最初のパスではRAMからラインをロードするため、時間が不十分です。
階段のように、長さの異なる列を通過するものを見たいです。 ステップの性質を判断するために、直接キャッシュと連想キャッシュの行渡しの例を考えます。複数連想キャッシュの場合は、直接マッピングキャッシュと連想キャッシュの平均になります。
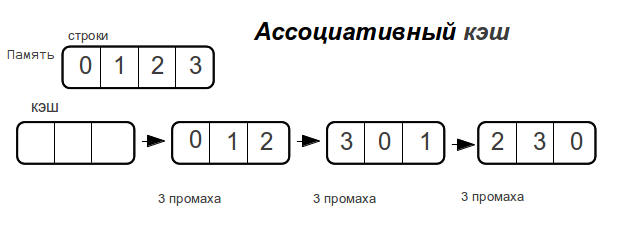
連想キャッシュ
データのサイズがキャッシュのサイズを超えるとすぐに、
メモリがアクセスされるたびに、完全連想キャッシュがミスします。
ダイレクトキャッシュ
さまざまな行サイズを考慮してください。 -プロセッサが行の次のパスで配列の要素にアクセスするために費やすミスの最大数を示します。

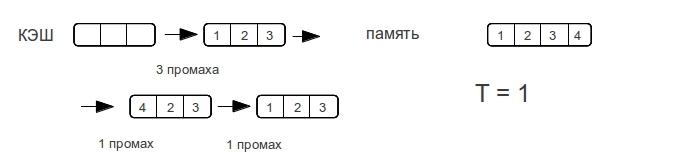
ご覧のとおり、メモリへのアクセス時間は急激には増加しませんが、データ量が増加します。 データのサイズがキャッシュのサイズを超えるとすぐに、メモリへのアクセスごとにミスが発生します。
したがって、連想キャッシュではステップは垂直になり、ダイレクトキャッシュではキャッシュの2倍のサイズまで徐々に増加します。 複数のアソシエイティブキャッシュは、アクセス時間がダイレクトよりも優れていることができないという理由だけで、中間ケースである「カスプ」になります。
メモリについて話す場合、最も高速なのはキャッシュであり、その後に動作可能なキャッシュが続きます。最も遅いのはスワップであり、今後はそれについて説明しません。 同様に、異なるキャッシュレベル(今日のプロセッサでは2〜3個のキャッシュレベルがあります)には、異なるメモリ応答速度があります。レベルが高いほど、応答速度は遅くなります。 したがって、ラインがキャッシュの第1レベルに配置されている場合(これは完全に関連性があります)、応答時間は、第1レベルキャッシュのサイズを大幅に超えるラインの応答時間よりも短くなります。 したがって、行サイズからのメモリ応答時間のグラフには、いくつかのプラトーがあります-メモリ応答のプラトー*と、異なるキャッシュレベルによって引き起こされるプラトーです。
*関数プラトー-{i:x、f(xi)-f(xi + 1)<eps:eps→0}
さあ始めましょう
実装には、C(ANSI C99)を使用します。
迅速に記述されたコード、異なる長さ(10 mb未満)の通常の通過が繰り返し実行されました。 (セマンティックロードを運ぶプログラムの小さな断片を提供します)。
for (i = 0; i < 16; i++) { for (j = 0; j < L_STR; j++) A[j]++; }
チャートを見ると、大きな一歩が見えています。 しかし、理論的にはすべてが判明し、素晴らしいだけです。 あなたは理解する必要があります:これは何のために起こっているのですか? そして、それを修正する方法は?
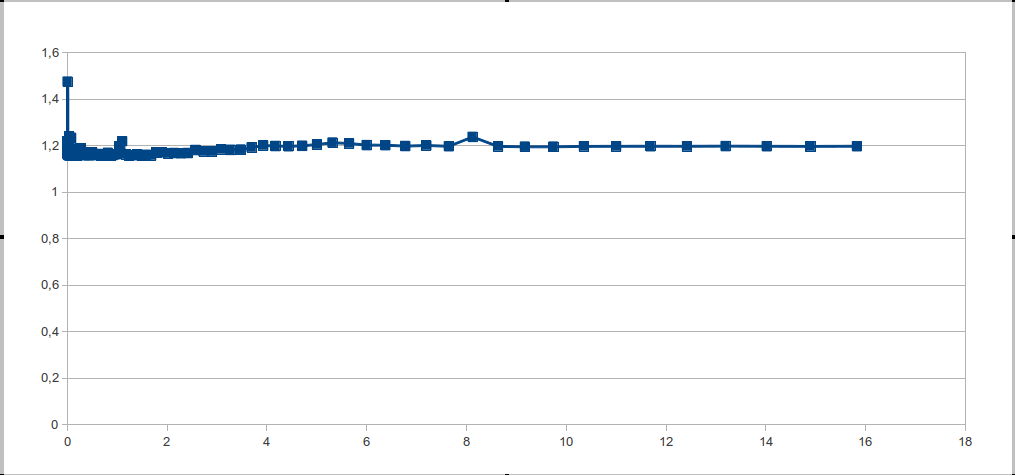
明らかに、これは2つの理由で発生する可能性があります。プロセッサにメモリキャッシュがないか、プロセッサがメモリアクセスを非常によく推測するかのいずれかです。 最初のオプションはフィクションに近いため、すべての理由はヒットの適切な予測です。
事実、今日ではトップエンドプロセッサとはかけ離れており、空間的局所性の原理に加えて、メモリへのアクセスの順序で算術的な進行も予測しています。 したがって、メモリアクセスをランダム化する必要があります。
ランダム化された配列の長さは、大きな粒度の呼び出しを取り除くためにメインラインの長さに匹敵しなければなりません。配列の長さは2の累乗であってはなりません。 粒度が素数である場合を含め、粒度定数を設定することをお勧めします。これにより、オーバーレイの影響を回避できます。 そして、ランダム化された配列の長さは、文字列の長さの関数です。
for (i = 0; i < j; i++) { for (m = 0; m < L; m++) { for (x = 0; x < M; x++){ v = A[ random[x] + m ]; } } }
その後、最初に議論されたこのような待望の「絵」に驚きました。
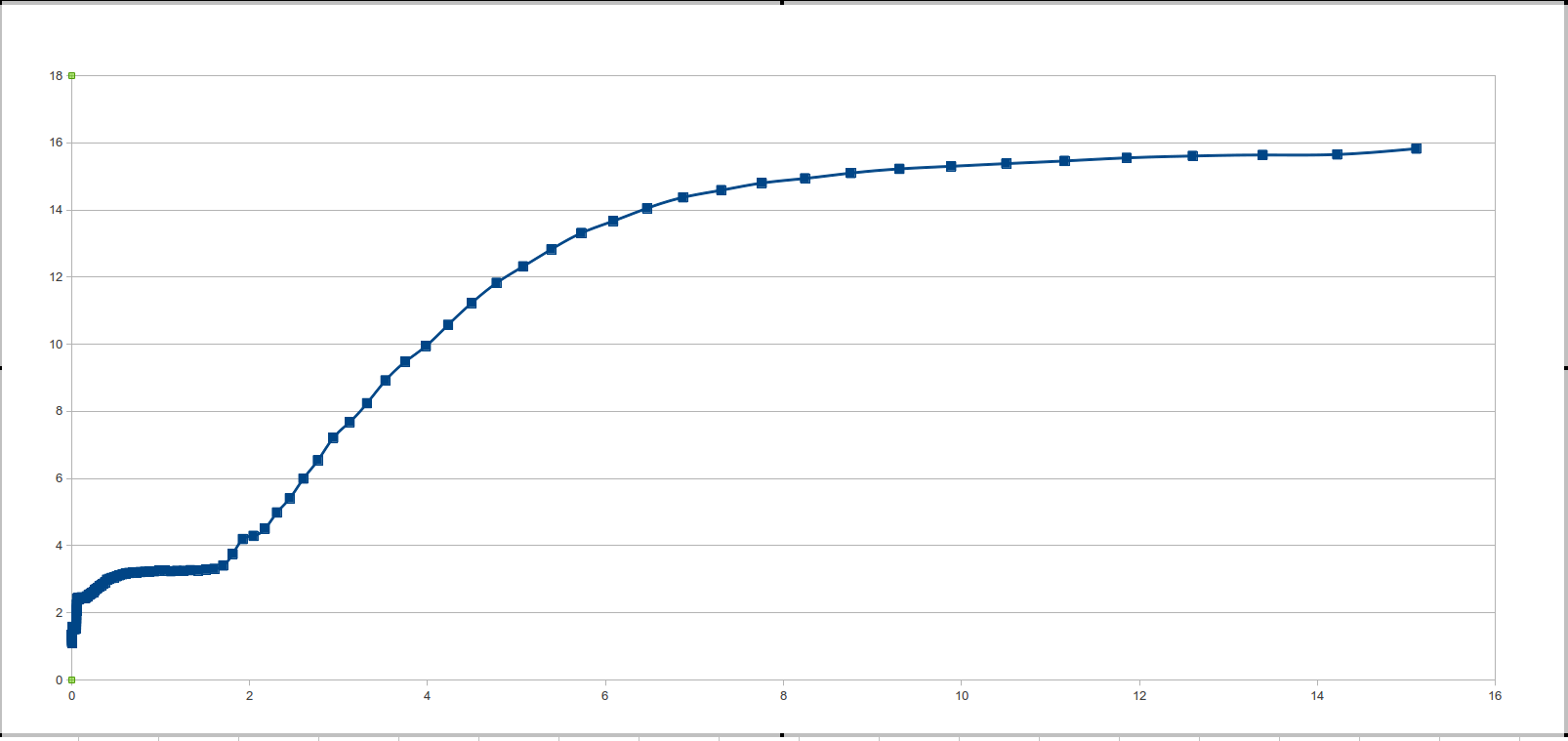
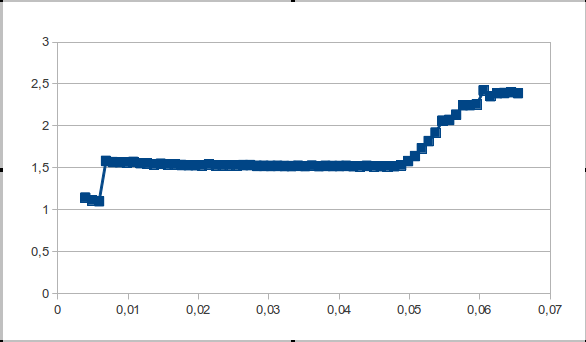
プログラムは、テストとデータ処理の2つの部分に分かれています。 自分でペンで2回実行または実行するスクリプトを3行で記述します。
Linuxでのsize.sファイルのリスト
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> #define T char #define MAX_S 0x1000000 #define L 101 volatile TA[MAX_S]; int m_rand[0xFFFFFF]; int main (){ static struct timespec t1, t2; memset ((void*)A, 0, sizeof (A)); srand(time(NULL)); int v, M; register int i, j, k, m, x; for (k = 1024; k < MAX_S;) { M = k / L; printf("%g\t", (k+M*4)/(1024.*1024)); for (i = 0; i < M; i++) m_rand[i] = L * i; for (i = 0; i < M/4; i++) { j = rand() % M; x = rand() % M; m = m_rand[j]; m_rand[j] = m_rand[i]; m_rand[i] = m; } if (k < 100*1024) j = 1024; else if (k < 300*1024) j = 128; else j = 32; clock_gettime (CLOCK_PROCESS_CPUTIME_ID, &t1); for (i = 0; i < j; i++) { for (m = 0; m < L; m++) { for (x = 0; x < M; x++){ v = A[ m_rand[x] + m ]; } } } clock_gettime (CLOCK_PROCESS_CPUTIME_ID, &t2); printf ("%g\n",1000000000. * (((t2.tv_sec + t2.tv_nsec * 1.e-9) - (t1.tv_sec + t1.tv_nsec * 1.e-9)))/(double)(L*M*j)); if (k > 100*1024) k += k/16; else k += 4*1024; } return 0; }
ファイルサイズのリスト(Windowsの場合)
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> #include <iostream> #include <Windows.h> using namespace std; #define T char #define MAX_S 0x1000000 #define L 101 volatile TA[MAX_S]; int m_rand[0xFFFFFF]; int main (){ LARGE_INTEGER freq; LARGE_INTEGER time1; LARGE_INTEGER time2; QueryPerformanceFrequency(&freq); memset ((void*)A, 0, sizeof (A)); srand(time(NULL)); int v, M; register int i, j, k, m, x; for (k = 1024; k < MAX_S;) { M = k / L; printf("%g\t", (k+M*4)/(1024.*1024)); for (i = 0; i < M; i++) m_rand[i] = L * i; for (i = 0; i < M/4; i++) { j = rand() % M; x = rand() % M; m = m_rand[j]; m_rand[j] = m_rand[i]; m_rand[i] = m; } if (k < 100*1024) j = 1024; else if (k < 300*1024) j = 128; else j = 32; QueryPerformanceCounter(&time1); for (i = 0; i < j; i++) { for (m = 0; m < L; m++) { for (x = 0; x < M; x++){ v = A[ m_rand[x] + m ]; } } } QueryPerformanceCounter(&time2); time2.QuadPart -= time1.QuadPart; double span = (double) time2.QuadPart / freq.QuadPart; printf ("%g\n",1000000000. * span/(double)(L*M*j)); if (k > 100*1024) k += k/16; else k += 4*1024; } return 0; }
一般的に、すべてが明確であると思いますが、いくつかの点を明記したいと思います。
配列Aはvolatileとして宣言されています-このディレクティブは、配列Aへの呼び出しが常に存在することを保証します。つまり、オプティマイザーもコンパイラも「それらを切り捨て」ません。 また、時間を測定する前に計算負荷全体が実行されるため、バックグラウンド効果を減らすことができます。
ファイルは、Ubuntu 12.04およびgcc 4.6コンパイラでアセンブラーに変換されます-サイクルが保存されます。
データ処理
データ処理では、デリバティブを使用するのが論理的です。 そして、微分の次数が増加すると、ノイズが増加するという事実にもかかわらず、二次導関数とその特性が使用されます。 二次導関数がどんなに騒々しくても、二次導関数の符号にのみ興味があります。
2次導関数がゼロより大きいすべての点を見つけます(数値的に考慮されることに加えて、2次導関数は非常にノイズが多いため、多少の誤差があります)。 関数の二次導関数の符号のキャッシュサイズへの依存性の関数を定義します。 この関数は、2次導関数の符号がゼロより大きいポイントで値1を取り、2次導関数の符号がゼロ以下の場合はゼロを取ります。
「テイクオフ」ポイントは、各ラングの始まりです。 また、データを処理する前に、データのセマンティックロードを変更しないが、顕著なノイズを作成する単一の外れ値を削除する必要があります。
リストファイルdata_pr.s
#include <stdio.h> #include <stdlib.h> #include <math.h> double round (double x) { int mul = 100; if (x > 0) return floor(x * mul + .5) / mul; else return ceil(x * mul - .5) / mul; } float size[112], time[112], der_1[112], der_2[112]; int main(){ size[0] = 0; time[0] = 0; der_1[0] = 0; der_2[0] = 0; int i, z = 110; for (i = 1; i < 110; i++) scanf("%g%g", &size[i], &time[i]); for (i = 1; i < z; i++) der_1[i] = (time[i]-time[i-1])/(size[i]-size[i-1]); for (i = 1; i < z; i++) if ((time[i]-time[i-1])/(size[i]-size[i-1]) > 2) der_2[i] = 1; else der_2[i] = 0; //comb for (i = 0; i < z; i++) if (der_2[i] == der_2[i+2] && der_2[i+1] != der_2[i]) der_2[i+1] = der_2[i]; for (i = 0; i < z-4; i++) if (der_2[i] == der_2[i+3] && der_2[i] != der_2[i+1] && der_2[i] != der_2[i+2]) { der_2[i+1] = der_2[i]; der_2[i+2] = der_2[i]; } for (i = 0; i < z-4; i++) if (der_2[i] == der_2[i+4] && der_2[i] != der_2[i+1] && der_2[i] != der_2[i+2] && der_2[i] != der_2[i+3]) { der_2[i+1] = der_2[i]; der_2[i+2] = der_2[i]; der_2[i+3] = der_2[i]; } // int k = 1; for (i = 0; i < z-4; i++){ if (der_2[i] == 1) printf("L%d = %g\tMb\n", k++, size[i]); while (der_2[i] == 1) i++; } return 0; }
テスト
CPU / OS /カーネルバージョン/コンパイラ/コンパイルキー-テストごとに表示されます。
-
Intel Pentium CPU P6100 @ 2.00GHz / Ubuntu 12.04 / 3.2.0-27-generic / gcc -Wall -O3 size.c -lrt
L1 = 0.05 Mb
L2 = 0.2 Mb
L3 = 2.7 Mb
- すべての良いテストを行うわけではありませんが、レーキについてもっと話しましょう
「熊手」について話しましょう
Intel Xeonサーバープロセッサ2.4 / L2 = 512 kb / Windows Server 2008でのデータ処理中に検出されたレーキ
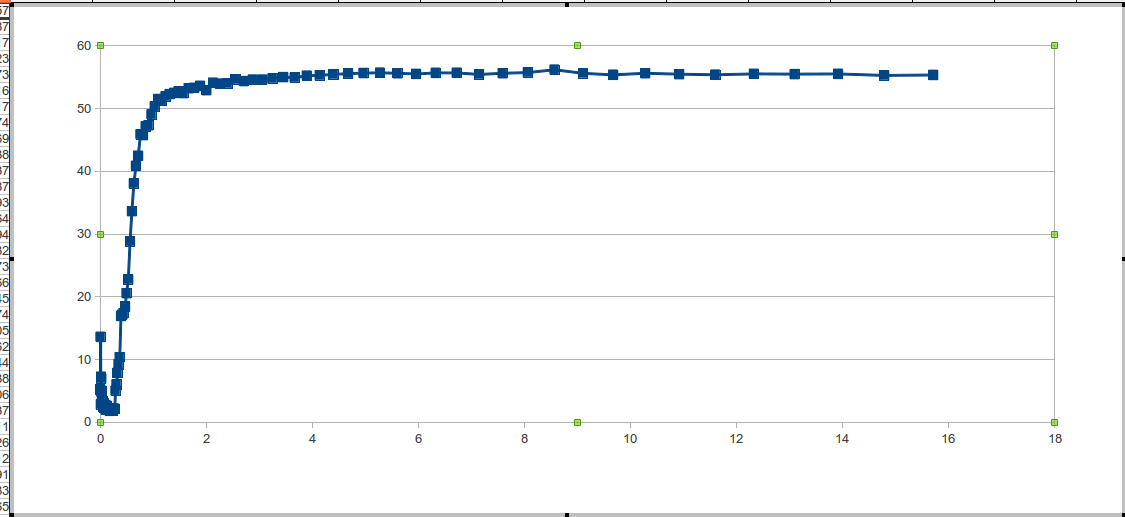
問題は、プラトーの終了間隔にある少数のポイントです。したがって、2次導関数のジャンプは見えず、ノイズと見なされます。
この問題を最小二乗法で解決するか、プラトーゾーンを決定するプロセスでテストを実行できます。
この問題の解決策に関するご意見をお聞かせください。
参照資料
- マカロフA.V. コンピュータアーキテクチャと低レベルプログラミング。
- Ulrich Drepperすべてのプログラマーがメモリについて知っておくべきこと