エントリー
これは、計算幾何学に関する私の記事の第2部です。 タスクはもう少し複雑になるので、この記事は前の記事よりも興味深いと思います。
線、光線、線分に対する点の相対的な位置から始めましょう。
タスク番号1
ポイントとラインの相対位置を決定します。ラインの上、ラインの上、ラインの下にあります。
解決策
線が方程式ax + by + c = 0で与えられる場合、解くべきものは何もないことは明らかです。 線の方程式の点の座標を置き換えて、それが等しいかどうかを確認するだけで十分です。 ゼロより大きい場合、ポイントは上半平面にあります。ゼロに等しい場合、ポイントは直線上にあり、ゼロより小さい場合、ポイントは下半平面にあります。 興味深いケースは、2点の座標が与えられて線が与えられたとき、それらをP 1 (x 1 、y 1 )、P 2 (x 2 、y 2 )と呼びます。 この場合、係数a、b、cを安全に見つけて、前の引数を適用できます。 しかし、私たちは最初に考えなければなりません、私たちはそれを必要としますか? もちろん違います! 斜めの作品で述べたように、これは計算幾何学のまさに真珠です。 それを適用しましょう。 最初のベクトルから2番目のベクトルへの回転が反時計回りの場合、2つのベクトルのスキュー積は正であり、ベクトルが共線の場合はゼロに等しく、回転が時計回りの場合は負になります。 したがって、ベクトルP 1 P 2とP 1 Mのスキュー積を計算し、その符号で結論を出すだけで十分です。

タスク番号2
ポイントがビームに属しているかどうかを判別します。
解決策
光線とは何かを思い出しましょう。光線は直線であり、一方の点で制限され、他方では無限です。 つまり、光線はいくつかの開始点とその上にある任意の点によって定義されます。 点P 1 (x 1 、y 1 )を光線の始まりとし、P 2 (x 2 、y 2 )を光線に属する任意の点とします。 点が光線に属している場合、これらの点を通過する線に属しているが、その逆ではないことは明らかです。 したがって、直線に属することは、必要ですが、光線に属するための十分な条件ではありません。 したがって、スキュー製品のチェックから逃れることはできません。 十分な条件のために、同じベクトルのスカラー積を計算することも必要です。 ゼロ未満の場合、ポイントはレイに属しません;負でない場合、ポイントはレイ上にあります。 なぜそう 写真を見てみましょう。

したがって、ポイントM(x、y)が開始点P 1 (x 1 、y 1 )の光線上にあるためには、P 2 (x 2 、y 2 )が光線上にあり、2つの条件が必要で十分です。
1. [P 1 P 2 、P 1 M] = 0-斜交積(点は線上にあります)
2.(P 1 P 2 、P 1 M)≥0-スカラー積(点は光線上にあります)
タスク番号3
ポイントがセグメントに属しているかどうかを判別します。
解決策
点P 1 (x 1 、y 1 )、P 2 (x 2 、y 2 )を特定のセグメントの端点とします。 この場合も、ポイントがセグメントに属するための必要条件は、P 1 、P 2を通る線に属することです。 次に、ポイントがポイントP 1とP 2の間にあるかどうかを判断する必要があります。そのためには、今回だけ異なるベクトルのスカラー積が必要です:(MP 1 、MP 2 )。 ゼロ以下の場合、ポイントはセグメント上にあり、そうでない場合はセグメントの外側にあります。 なぜそう 写真を見てみましょう。

したがって、点M(x、y)が端P 1 (x 1 、y 1 )、P 2 (x 2 、y 2 )を持つセグメント上にあるためには、次の条件が満たされることが必要で十分です。
1. [P 1 P 2 、P 1 M] = 0-斜交積(点は線上にあります)
2.(MP 1 、MP 2 )≤0-スカラー積(ポイントはP 1とP 2の間にあります)
タスク番号4
2点の相対位置は比較的直線です。
解決策
この問題では、直線を基準にして片側または異なる側の2点を決定する必要があります。
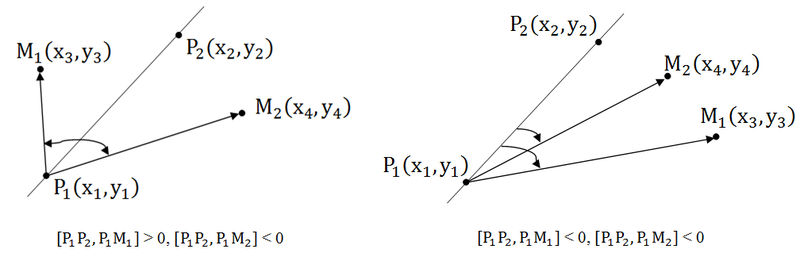
ポイントが比較的直線の反対側にある場合、スキュー製品には異なる符号が付けられます。つまり、製品は負になります。 点が直線に対して片側にある場合、スキュー製品の符号は一致します。これは、製品が正であることを意味します。
だから:
1. [P 1 P 2 、P 1 M 1 ] * [P 1 P 2 、P 1 M 2 ] <0-点は反対側にあります。
2. [P 1 P 2 、P 1 M 1 ] * [P 1 P 2 、P 1 M 2 ]> 0-点は片側にあります。
3. [P 1 P 2 、P 1 M 1 ] * [P 1 P 2 、P 1 M 2 ] = 0-点の1つ(または2つ)が線上にあります。
ところで、直線と線分との交点の存在を判断する問題は、同じ方法で解決されます。 より正確には、これは同じ問題です。セグメントの端が線の反対側にあるとき、またはセグメントの端が線上にあるときに、セグメントと線が交差します。つまり、[P 1 P 2 、P 1 M 1 ] * [P 1 P 2 、P 1 M 2 ]≤0。
タスク番号5
2本の線が交差するかどうかを判断します。
解決策
線が一致しないと仮定します。 線が平行である場合にのみ交差しないことは明らかです。 したがって、並列条件が見つかったので、線が交差するかどうかを判断できます。
線が方程式a 1 x + b 1 y + c 1 = 0およびa 2 x + b 2 y + c 2 = 0によって与えられると仮定します。次に、平行線の条件はa 1 b 2 -a 2 b 1 = 0。
ラインがポイントP 1 (x 1 、y 1 )、P 2 (x 2 、y 2 )、M 1 (x 3 、y 3 )、M 2 (x 4 、y 4 )によって与えられる場合、それらの並列性の条件はベクトルP 1 P 2とM 1 M 2のスキュー積をチェックする場合:ゼロの場合、線は平行です。
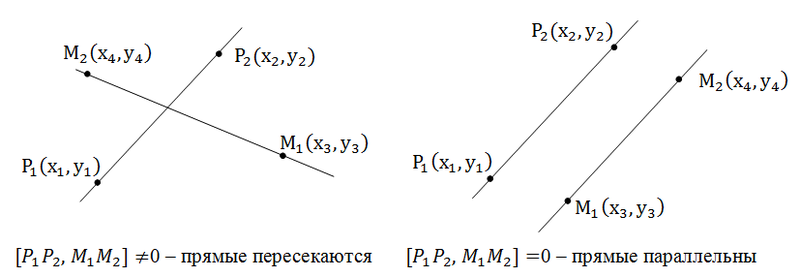
一般に、線がそれらの方程式によって与えられる場合、方向ベクトルと呼ばれるベクトル(-b 1 、a 1 )、(-b 2 、a 2 )のスキュー積もチェックします。
タスク番号6
2つのセグメントが交差するかどうかを判断します。
解決策
私はこのタスクが本当に好きです。 各セグメントの端が他のセグメントの異なる側にある場合、セグメントは交差します。 写真を見てみましょう:
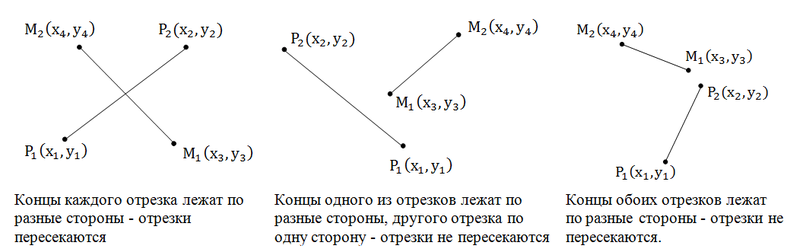
そのため、各セグメントの端が他のセグメントの相対端の反対側にあることを確認する必要があります。 ベクトルのスキュー積を使用します。 最初の写真を見てください:[P 1 P 2 、P 1 M 2 ]> 0、[P 1 P 2 、P 1 M 1 ] <0 => [P 1 P 2 、P 1 M 2 ] * [P 1 P 2 、P 1 M 1 ] <0。同様に
[M 1 M 2 、M 1 P 1 ] * [M 1 M 2 、M 1 P 2 ] <0。 そして、ベクトル積がゼロに正確に等しいが、セグメントが交差しない次のケースが可能であるため:

したがって、もう1つチェックを行う必要があります。つまり、各セグメントの少なくとも一方の端が別の端に属している(ポイントがセグメントに属している)かどうかです。 この問題はすでに解決済みです。
そのため、セグメントに共通のポイントを持たせるには、必要かつ十分です:
1.セグメントの端は、別のセグメントに対して異なる側にあります。
2. 1つのセグメントの少なくとも1つの端が別のセグメントに属します。
タスク番号7
ポイントからラインまでの距離。
解決策
線が2つの点P 1 (x 1 、y 1 )およびP 2 (x 2 、y 2 )によって与えられるとします。
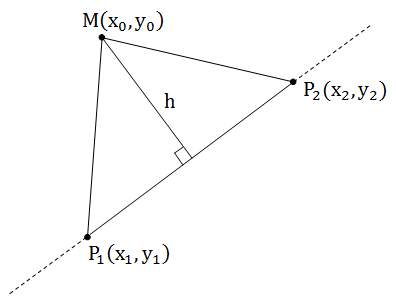
前の記事で、幾何学的に歪んだ積が平行四辺形の方向付けられた領域であるため、SP 1 P 2 M = 0.5 * [P 1 P 2 、P 1 M]という事実について説明しました。 一方、すべての生徒は、三角形の面積を求めるための公式を知っています:半分のベースから高さ。
S P 1 P 2 M = 0.5 * h * P 1 P 2 。
これらの領域を等しくすると、

最初の領域が方向付けられているため、モジュロが取られます。
直線が方程式ax + by + c = 0で与えられる場合、与えられた直線に垂直な点Mを通る直線の方程式は次のとおりです。a(y-y 0 )-b(x-x 0 )= 0。方程式、それらの交点を見つけ、開始点から見つかったものまでの距離を計算します。正確にρ=(ax 0 + by 0 + c)/√(a 2 + b 2 )になります。
タスク番号8
ポイントからビームまでの距離。
解決策
このタスクは、この場合に発生する可能性があるという点で前のタスクとは異なります。そのため、ポイントからの垂線はビームに当たらず、その連続になります。
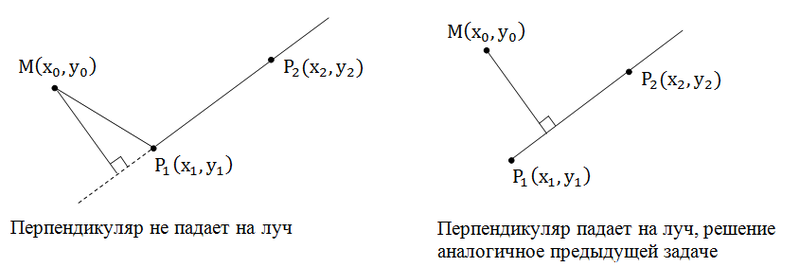
垂線がビームに当たらない場合は、ポイントからビームの始点までの距離を見つける必要があります-これが問題の答えになります。
垂線がビームに当たるかどうかを判断する方法は? 垂線がビームに当たらない場合、角度MP 1 P 2は鈍角になります。 したがって、ベクトルのスカラー積の符号により、垂線が光線に当たるかどうかを判断できます。
1.(P 1 M、P 1 P 2 )<0垂線がビームに当たらない
2.(P 1 M、P 1 P 2 )≥0垂線がビームに当たる
タスク番号9
ポイントからラインまでの距離。
解決策
前の問題と同様に推論します。 垂線がセグメントに当たらない場合、答えはこのポイントからセグメントの端までの距離の最小値になります。

垂線がセグメントに当たるかどうかを判断するには、前のタスクと同様に、ベクトルのスカラー積を使用する必要があります。 垂線がセグメントに当たらない場合、角度MP 1 P 2または角度MP 2 P 1は鈍角になります。 したがって、スカラー積の符号により、垂線がセグメントに当たるかどうかを判断できます。
(P 1 M、P 1 P 2 )<0または(P 2 M、P 2 P 1 )<0の場合、垂線はセグメントに該当しません。
タスク番号10
線と円上の点の数を決定します。
解決策
直線と円には、0、1、または2つの交点があります。 写真を見てみましょう:
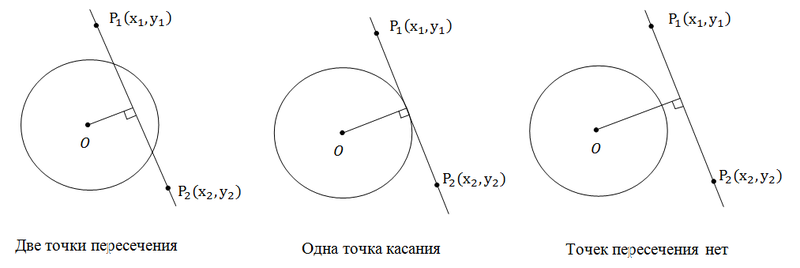
ここでは、図面から、すべてが明確です。 円の中心から線までの距離が円の半径より小さい場合、2つの交点があります。 中心から線までの距離が半径に等しい場合の1つのタッチポイント。 最後に、円の中心から線までの距離が円の半径よりも大きい場合、単一の交点ではありません。 点から線までの距離を見つける問題はすでに解決されているため、この問題も解決されています。
タスク番号11
2つの円の相対位置。
解決策
円の配置の可能なケース:交差、接触、交差しない。
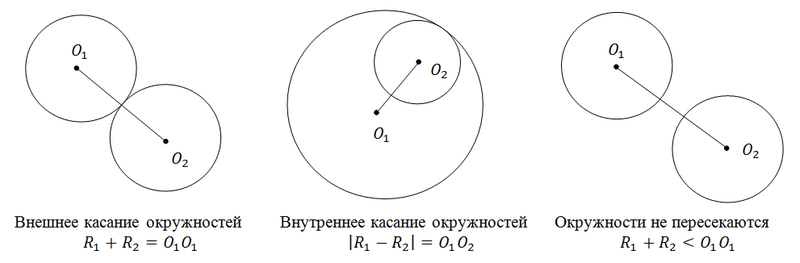
円が交差する場合を考慮し、それらの交差の面積を見つけます。 かなりの時間をかけて解決したので、このタスクが大好きです(1年前-ずっと前でした)。


今、セクターとセグメントが何であるかを思い出してください。
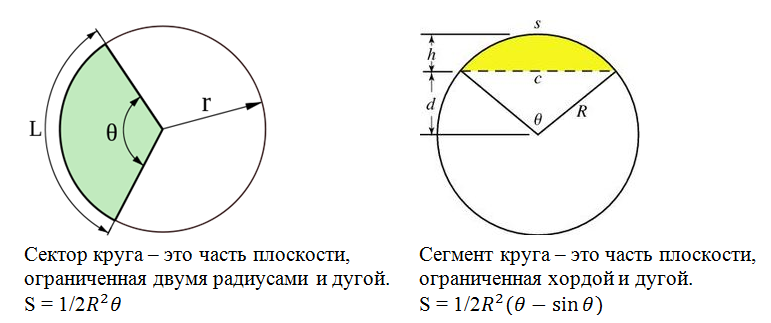
円の交点は2つのセグメントO 1 ABとO 2 ABで構成されます。
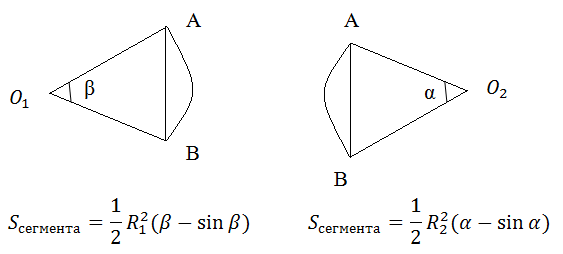
これらのセグメントおよびすべての領域を合計する必要があると思われます。 ただし、すべてがそれほど単純ではありません。 これらの式が常に真であるかどうかを判断することも必要です。 いいえ判明!
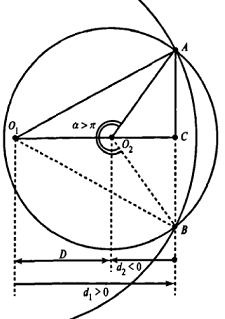
2番目の円O 2の中心が点Cと一致する場合を考えます。この場合、値αに対してd 2 = 0およびα=πです。 この場合、1/2πR2 2の面積を持つ半円があります。
次に、2番目の円O 2の中心が点O 1とCの間にある場合を考えます。この場合、d 2の負の値を取得します。 d 2の負の値を使用すると、αの負の値になります。 この場合、正解にα2πを追加する必要があります。
おわりに
まあ、それだけです。 すべてを検討したわけではありませんが、オブジェクトの相対位置に関する計算幾何学で最も頻繁に発生する問題です。楽しんでいただけましたでしょうか。