みなさんこんにちは。 今週、 機械学習コースで、Andrew Ng教授は、データの特徴空間の次元を削減できる主成分法について聴衆に語りました 。 しかし、残念なことに、彼は行列の固有ベクトルと固有値の計算方法については話しませんでした。単純に、それは複雑であると言い、matlab / octave関数[USV] = svd（a）を使用して助言しました。



私のプロジェクトでは、c＃でこのメソッドを実装する必要がありましたが、今日はそれを行いました。 主要なコンポーネントの方法自体は非常にエレガントで美しいため、このすべての背後にある数学を理解していない場合、これはシャーマニズムと呼ぶことができます。 行列の固有ベクトルを計算する際の問題は、正確な値をすばやく計算する方法がないため、外に出なければならないことです。 抜け出すためのこれらの方法の1つについてお話ししたいと思います。また、この手順を実行するc＃コードも提供します。 猫をお願いします。

主成分法（これまでのコードなし）

パート1：アルゴリズムの初期化。 入力はデータの配列であり、データを削減する必要があるスペースの次元です。

1. 共分散行列が計算されます（この行列には素晴らしい特性があります-対称的であり、これは非常に便利です）
2. 行列の固有ベクトルが計算されます
3. 固有ベクトルの最初のenが選択されます。enは、特徴空間の次元を削減する必要がある次元と同じ次元です。 選択したベクトルを垂直に記述し、マトリックスに組み立てることができます

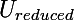
パート2：入力ベクトルの次元を減らす。 初期化ステップで使用されるデータ配列のような次元のベクトルが入力に供給されます。 出力は低次元のベクトル（または固有ベクトルのサンプルによって形成された正規直交基底への入力ベクトルの投影）です。

• 入力ベクトルに固有ベクトルのサンプルからのすべてのベクトルをスカラーで乗算すると、 縮小ベクトルが得られます。

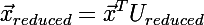
パート3：ベクトルの次元を復元します（もちろん情報が失われます）。 入力は、ベクトルを削減した次元に等しい次元のベクトルです。 出力は元の次元のベクトルです。

• 行列を転置する場合 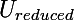次に、前のステップで入力ベクトルの次元と同じ数の行が含まれ、目的のベクトルが式によって復元されます。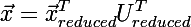

ご覧のとおり、共分散行列と固有ベクトルを計算する際の計算の複雑さはすべて初期化ステップにあります。 共分散行列の計算については説明しません。なぜなら、 定義により単純に計算されます。 行列の固有ベクトルを計算するためのいくつかのアルゴリズムを研究した後、QR分解の反復法に決めました。 これには大きな制限があり、対称行列に対してのみ多少正確な結果が得られますが、幸運なことに:)、共分散行列はまさにそれです。 このアルゴリズムの2番目の制限は、行列がフルランクでなければならないことです。

QR分解

固有ベクトルを検索する反復QRメソッドは明らかにQR分解を使用するため、最初にこのプロセスを実装する必要があります。 このプロセスを実装するために、 Graham-Schmidtアルゴリズムが選択されました。



これを行うには、ベクトルaのベクトルbへの射影を計算する関数が必要です。 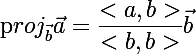、ここで<>-ベクトルのスカラー積を示します。

public static double[] VectorProjection(double[] a, double[] b) { double k = ScalarVectorProduct(a, b)/ScalarVectorProduct(b, b); return ScalarToVectorProduct(k, b); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

テキストのコードサイズが重要な基準を超えないように、ScalarVectorProductなどの単純な関数についても説明しません。



したがって、実際のQR分解手順IList <double []> DecompositionGS（double [] [] a）は行列入力を受け取り、それに応じて2つの行列を返します。

1. 最初の列には、次のような正規直交基底が含まれています。 ;
2. 2番目の行列は上三角になります。

まず、マトリックスを列に分割し、 avリストに書き込みます。

 List<double[]> av = new List<double[]>(); foreach (double[] vector in DecomposeMatrixToColumnVectors(a)) { av.Add(vector); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2つの補助リストを初期化します。

 List<double[]> u = new List<double[]>(); u.Add(av[0]); List<double[]> e = new List<double[]>(); e.Add(ScalarToVectorProduct(1 / NormOfVector(u[0]), u[0]));
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらは、アルゴリズム図で使用されているのと同じ名前の同じリストです。





初期化後、最初のuとeが計算され、ループ内で次の値を計算し続けます。

 for (int i = 1; i < a.Length; i++) { double[] projAcc = new double[a.Length]; for (int j = 0; j < projAcc.Length; j++) { projAcc[j] = 0; } for (int j = 0; j < i; j++) { double[] proj = VectorProjection(av[i], e[j]); for (int k = 0; k < projAcc.Length; k++) { projAcc[k] += proj[k]; } } double[] ui = new double[a.Length]; for (int j = 0; j < ui.Length; j++) { ui[j] = a[j][i] - projAcc[j]; } u.Add(ui); e.Add(ScalarToVectorProduct(1/NormOfVector(u[i]), u[i])); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、出力形式でデータを生成します。

 double[][] q = new double[a.Length][]; for (int i = 0; i < q.Length; i++) { q[i] = new double[a.Length]; for (int j = 0; j < q[i].Length; j++) { q[i][j] = e[j][i]; } } double[][] r = new double[a.Length][]; for (int i = 0; i < r.Length; i++) { r[i] = new double[a.Length]; for (int j = 0; j < r[i].Length; j++) { if (i >= j) { r[i][j] = ScalarVectorProduct(e[j], av[i]); } else { r[i][j] = 0; } } } r = Transpose(r); List<double[][]> res = new List<double[][]>(); res.Add(q); res.Add(r); return res;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

やった！ 次に、このためのテストが必要です。

 [Test(Description = "Test of QRDecompositionGS")] public void QRDecompositionGSTest() { double[][] a = new double[][] { new double[] {12, -51, 4}, new double[] {6, 167, -68}, new double[] {-4, 24, -41} }; IList<double[][]> res = LinearAlgebra.QRDecompositionGS(a); double[][] expQ = new double[][] { new double[] {6.0/7, -69.0/175, -58.0/175}, new double[] {3.0/7, 158.0/175, 6.0/175}, new double[] {-2.0/7, 6.0/35, -33.0/35} }; double[][] expR = new double[][] { new double[] {14, 21, -14}, new double[] {0, 175, -70}, new double[] {0, 0, 35} }; Assert.True(Helper.AreEqualMatrices(expQ, res[0], 0.0001), "expQ != Q"); Assert.True(Helper.AreEqualMatrices(expR, res[1], 0.0001), "expR != R"); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Helper.AreEqualMatrices関数は、要素ごとの行列を3番目のパラメーターまで比較します。

反復QR法

反復QR法は、顕著な定理に基づいており、その本質は、行列Aを次のようにゼロに初期化することです。 そして、次のプロセスを無限に繰り返します：

1. 
2. 

そして、得られたすべてのQを乗算すると、結果は行列になります。列には、元の行列の固有ベクトルがあり、その値はより正確で、プロセスに時間がかかります。 言い換えれば、反復回数が無限になる傾向があるため、積 固有ベクトルの値を正確にする傾向があります。 同時に、後者 主対角線上には、当然のことながら、行列の固有値が含まれます。 このアルゴリズムは、対称行列に対してのみ多少正確に機能することを思い出してください。



そのため、QR反復メソッドIList <double [] []> EigenVectorValuesExtractionQRIterative（double [] [] a、double precision、int maxIterations）は、行列自体を通過する入力としていくつかのパラメーターを受け取ります。

• double precision-達成したい精度。固有ベクトルの値の変化がこの値以下の場合、アルゴリズムは停止します。
• int maxIterations-反復の最大数。

出力では、2つの行列を取得します。

1. 最初の列には、行列aの固有ベクトルが含まれています。
2. 主対角の2番目の行列には、行列aの固有値が含まれます。

そのため、アルゴリズムの記述を開始します。最初に、元の行列の固有ベクトルと固有値を含む行列を作成します。

 double[][] aItr = a; double[][] q = null;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そして、アルゴリズムが停止するまでループを実行します。

 for (int i = 0; i < maxIterations; i++) { IList<double[][]> qr = QRDecompositionGS(aItr); aItr = MatricesProduct(qr[1], qr[0]); if (q == null) { q = qr[0]; } else { double[][] qNew = MatricesProduct(q, qr[0]); bool accuracyAcheived = true; for (int n = 0; n < q.Length; n++) { for (int m = 0; m < q[n].Length; m++) { if (Math.Abs(Math.Abs(qNew[n][m]) - Math.Abs(q[n][m])) > accuracy) { accuracyAcheived = false; break; } } if (!accuracyAcheived) { break; } } q = qNew; if (accuracyAcheived) { break; } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

出力を生成します。

 List<double[][]> res = new List<double[][]>(); res.Add(q); res.Add(aItr); return res;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そしてもちろんテスト：

 [Test(Description = "Test of Eigen vectors extraction")] public void EigenVectorExtraction() { double[][] a = new double[][] { new double[] {1, 2, 4}, new double[] {2, 9, 8}, new double[] {4, 8, 2} }; IList<double[][]> ev = LinearAlgebra.EigenVectorValuesExtractionQRIterative(a, 0.001, 1000); double expEV00 = 15.2964; double expEV11 = 4.3487; double expEV22 = 1.0523; Assert.AreEqual(expEV00, Math.Round(Math.Abs(ev[1][0][0]), 4)); Assert.AreEqual(expEV11, Math.Round(Math.Abs(ev[1][1][1]), 4)); Assert.AreEqual(expEV22, Math.Round(Math.Abs(ev[1][2][2]), 4)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

固有ベクトルは反復ごとに方向を変えることができます。これは、座標の符号を変更することで確認できますが、これが必須ではないことは明らかです。

主成分法の実装

これで、サブジェクトの実装の準備がすべて整いました。



モデル（クラス）の非表示パラメーターは、ソースデータからの共分散行列の固有ベクトルのサブセットになります。

 private IList<double[]> _eigenVectors = null;
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

設計者は入力データの配列と次元を取得します。これには、符号のスペースとQR分解のパラメーターを削減する必要があります。 内部では、共分散行列が計算され、最初のいくつかの固有ベクトルが取得されます。 一般に、目的の情報損失パラメータに最適な固有ベクトル数を選択する方法があります。 情報を一定の割合しか失っていないので、どの次元にスペースを減らすことができますが、この手順を省略します。コースWebサイトのAndrew Ngによる講義でそれについて聞くことができます。

 internal DimensionalityReductionPCA(IList<double[]> dataSet, double accuracyQR, int maxIterationQR, int componentsNumber) { double[][] cov = BasicStatFunctions.CovarianceMatrixOfData(dataSet); IList<double[][]> eigen = LinearAlgebra.EigenVectorValuesExtractionQRIterative(cov, accuracyQR, maxIterationQR); IList<double[]> eigenVectors = LinearAlgebra.DecomposeMatrixToColumnVectors(eigen[0]); if (componentsNumber > eigenVectors.Count) { throw new ArgumentException("componentsNumber > eigenVectors.Count"); } _eigenVectors = new List<double[]>(); for (int i = 0; i < componentsNumber; i++) { _eigenVectors.Add(eigenVectors[i]); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、記事の最初から式を使用して直接変換と逆変換を実装します。

 public double[] Transform(double[] dataItem) { if (_eigenVectors[0].Length != dataItem.Length) { throw new ArgumentException("_eigenVectors[0].Length != dataItem.Length"); } double[] res = new double[_eigenVectors.Count]; for (int i = 0; i < _eigenVectors.Count; i++) { res[i] = 0; for (int j = 0; j < dataItem.Length; j++) { res[i] += _eigenVectors[i][j]*dataItem[j]; } } return res; } public double[] Reconstruct(double[] transformedDataItem) { if (_eigenVectors.Count != transformedDataItem.Length) { throw new ArgumentException("_eigenVectors.Count != transformedDataItem.Length"); } double[] res = new double[_eigenVectors[0].Length]; for (int i = 0; i < res.Length; i++) { res[i] = 0; for (int j = 0; j < _eigenVectors.Count; j++) { res[i] += _eigenVectors[j][i]*transformedDataItem[j]; } } return res; }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

テスト中

テストのために、小さなデータ配列を作成し、matlabの値を確認します（PCA =の自宅のコードを使用）。テスト用のクラスを作成します。

 [TestFixture(Description = "Test of DimensionalityReductionPCA")] public class DimensionalityReductionPCATest { private IList<double[]> _data = null; private IDataTransformation<double[]> _transformation = null; private double[] _v = null; [SetUp] public void SetUp() { _v = new double[] { 1, 0, 3 }; _data = new List<double[]>() { new double[] {1, 2, 23}, new double[] {-3, 17, 5}, new double[] {13, -6, 7}, new double[] {7, 8, -9} }; _transformation = new DimensionalityReductionPCA(_data, 0.0001, 1000, 2); } [Test(Description = "Test of DimensionalityReductionPCA transform")] public void DimensionalityReductionPCATransformTest() { double[] reduced = _transformation.Transform(_v); double[] expReduced = new double[] {-2.75008, 0.19959}; Assert.IsTrue(Helper.AreEqualVectors(expReduced, reduced, 0.001)); double[] reconstructed = _transformation.Reconstruct(reduced); double[] expReconstructed = new double[] {-0.21218, -0.87852, 2.60499}; Assert.IsTrue(Helper.AreEqualVectors(expReconstructed, reconstructed, 0.001)); }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

参照資料

• 機械学習コース
• 反復QRメソッドを説明する記事
• 記事の本文にあるウィキペディアのリンクの束