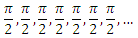
明らかな正解が提案されました。
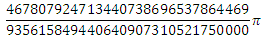
それがどのように受け取られたかを知らなかった人々のために、説明が提供されました。 させて
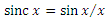（まあ、 x = 0の場合は1、重要ではありません）。 次に、系列の各メンバーは、チェーン内の次の積分の値です。
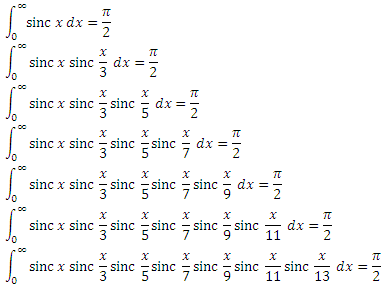
これまでのところ、すべてが順調に進んでいますが、その後突然：
原則として、これは私の数学の友人を楽しませるために十分ですが、そのような積分が一般的にどのように考慮され、なぜそのようなばかげた結果が得られるのかを知りたいと思いました。 他の誰かが昔を振り、ファンタンと一緒にマタンを覚えたいと思うなら、読んでください。
おとぎ話が語り始める
最初に、最初の積分を個別に見てみましょう。
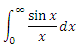
しばらく前、私は考えました：「ねえ、私は完全にマタンを忘れていません！ この積分を不定と見なして、制限を設定します。 確かに部品で数回、そして事は帽子にあります。 今、私は外部の助けなしに紙を決めることにします。」 私はあなたに警告したい：私の間違いを繰り返さないでください。 眠れぬ夜があなたを待っています、そして、あなたはディレクトリを見て、不定積分が初等関数でとられないことを見つけます。 彼のために、彼らは特別な機能さえ導入しました。
ただし、これらの特定の制限により、積分はさまざまな方法で取得できます。 最低限の基本的な知識を必要とする方法で進めます（最も厳しいのは、部品の同じ統合です）。 まず、突然の交換を行います。
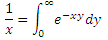
あなたは尋ねる：これはどこから来たのか、なぜ別の積分が必要なのか、それだけでは十分ではないのか？ 落ち着いていて、必要です（ラプラス変換の特性に精通している人は元気よく笑っています）。 元の式で置換を置き換え、統合順序を変更します。
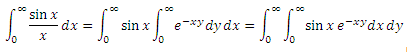
内部には、ほぼ古典的なdx積分があり、これが物理学の学生を怖がらせました。 部品の積分式を2回使用して、不定とみなすこともできます。 次に右側で、ある種の濁度を取得し、再び同じ積分に何かを乗算します。その結果、この積分の方程式を解いて答えを取得し、制限を設定することができます。 誰が気にかけ、自分でそれをし、完成した結果を怠finishedに書き留めます：
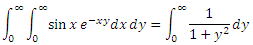
さて、これですべてが簡単になりました。これは、セカンダリスクールの積分テーブルであり、逆正接に相当します。 無限大、半分、ゼロ-ゼロで、答えが得られました。
ちなみに、積分は非常に優れているため、 ディリクレ積分と呼ばれます。 リンクから他の方法を見つけることができます。
すぐにおとぎ話が影響しますが、すぐに物事は行われません
次の旅行のために、4つの事柄が必要です：矩形関数、コサインフーリエ変換、畳み込み、およびParsevalの定理。 最初に、これらの素晴らしいことについていくつかの言葉を述べます。
矩形関数 -ゼロのようなステップがあります：
不連続点での値1/2は、主にフーリエ変換の特性を観察するために必要です;一般に、私たちの問題では、原理的ではありません。
コサインフーリエ変換 。 簡単にするために、数学的精度から少し逸脱し、大まかに定式化します。 十分に優れた偶関数f（x）の場合、次の関係が成り立ちます。
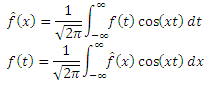
機能
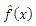また、f（x）のコサインフーリエ変換（FCT）と呼ばれます（fのイメージとも呼ばれます）。 つまり、コサイン変換からのコサイン変換により、元の関数f（x）が再び得られます。
信号処理に精通している人は、矩形関数のFCTが
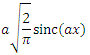。 これは、上記の式と学校の知識を使用して簡単に証明できます。 区間[-a、a]の外側の矩形関数はゼロに等しいため、この区間でcos（xt）dtを単純に積分できます。ここでは、変数とテーブル積分を単純に置き換えることができます。 上記のプロパティは、FCT 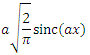長方形の関数です。
畳み込みは、信号処理がなくても実行できるもう1つの素晴らしい機能です。 2つの関数f 1 （x）およびf 2 （x）の場合、次のように畳み込み関数（アスタリスクで示される）を定義できます。
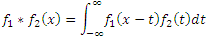
畳み込みには、それが愛されている素晴らしい特性があります。フーリエ変換は、それを乗算に変換し、乗算を畳み込みに変換します。 より正確には、2つの良い偶数関数の積のコサイン変換は、2つのpiの根で割った画像の畳み込みです。
。
Parsevalの定理は、信号エネルギーとそのスペクトルの等価性に関する非常にクールなステートメントであり、目的ごとに異なる方法で記述されています。 このバージョンが必要です：均等でかなり良い機能のために
。
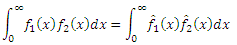Doseleva Makarは庭を掘っていたが、今ではMakarが地方にいる
素晴らしいシーケンスから2番目の積分を取ります。 多くの人がすでに推測しているように、Parsevalの定理を使用して、要因をFCTイメージに置き換えます。
積分の下の最初の長方形関数は、1より小さい引数の場合は1、1より大きい引数の場合は0です。 したがって、積分の制限を調整して積分から積分を削除することを妨げるものはありません。
積分の下に、高さ3、幅1/3の段差が残っていました。 3年生でもこのような積分を取ります。3と1/3を掛けるだけです。 1つは積分から残り、目的のパイが半分になりました！ したがって、私たちはほとんど正直にシリーズから2番目の積分を取りました。 これを非常に正直に行いたい人は、機能の良さを理解し、機能が優れていることを証明する必要があります。
さらに簡単にするために、このステップを積分の下でF 1 （x）として示し、そのグラフを描きます。
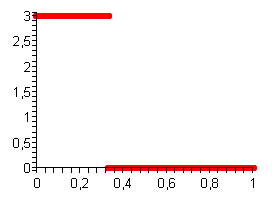
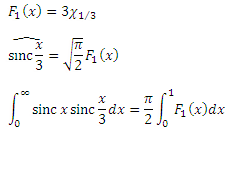
楽しみながら、3つの要素の積分を見ていきましょう。 Parsevalの定理を適用するために、2番目からのすべての要因を1つの要因と見なします。
。 最初の要因のイメージでは、すべてがすでに明確であり、2番目の要因のイメージは畳み込みによって表されます。
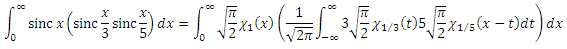
一見不気味です。 しかし、あなたは何かを上げ、何かを切り、私たちのF 1 （x）を置き換えることができます。 それから私達は得る：
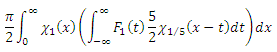
内部積分は、関数F 1 （x）の一種の「青みがかった」長方形フィルターにすぎません。各ポイントについて、近隣のすべての値をプラスマイナス5分の1だけ平均します。 繰り返しますが、統合の限界を突くことにより、矩形関数を取り除くことができます。 外部積分を使用して、同じ手順を実行します。 結果は次のとおりです。
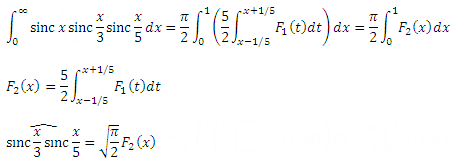
左側には関数F 2 （x）のグラフがありますが、これは実際には平滑化されたF 1 （x）です。 正規化されたカーネルに沿って関数を平滑化した後、その積分が変化しないことを証明するのは簡単です。 さて、実際には-∞から+∞までの積分について話していますが、偶数関数の場合、これはゼロからの積分にも当てはまります。 この場合、カーネルは-1/5から+1/5までのステップに5/2を掛けたものでした。 ステップの下の領域は単一であり、コアが正規化されていることを意味します。 ここでも、Photoshopの青と比較できます。青を適用した後、画像全体が明るくなったり暗くなったりすることはありません。 もしそうなら、積分F 2 （x）は積分F 1 （x）と正確に等しい、つまり1であるため、3番目の積分はパイ半分に等しくなります！
さらに、手順は非常に似ています。 4番目の積分を次のようにグループ化します。
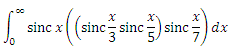。 最初に、括弧のパーセバル定理は畳み込みであり、 F 2 （x）に関して内部括弧のイメージを表現する方法をすでに知っています。 その後、すべてが前回と同じになり、結果として次のようになります。
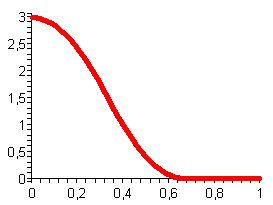
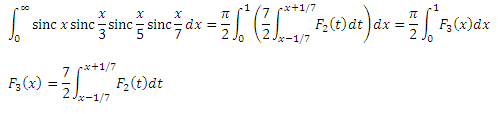
すでにF 3 （x）があります。これは実際には、 2 /7幅のカーネルを持つ平滑化されたF 2 （x）です。 カーネルは正規化されます。これは、積分F 3 （x）が積分F 2 （x）に等しいこと、つまり1であることを意味します。
素晴らしい、ナットのようなこれらの積分をクリックします。 しかし、理論的には、このようになると、それらはすべて無限に等しくなりますか？ さらに見てみましょう。 5番目の積分：
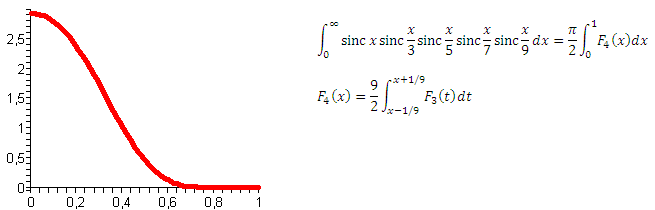
すべてが同じようです。 さて、6番目の積分：
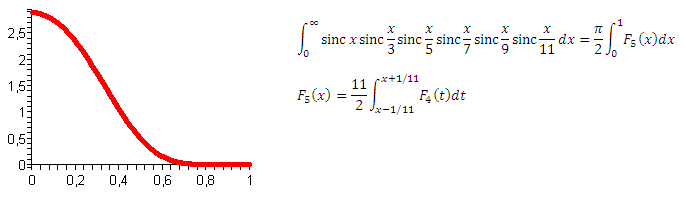
そして、問題はありません。 わかりました、7番目を取る：
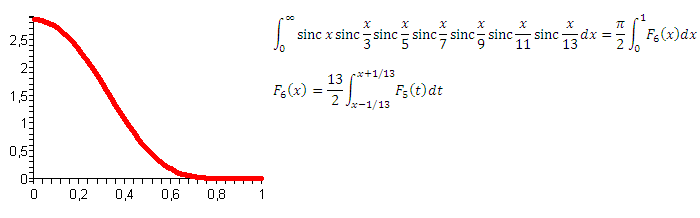
新しいものはありません！ さて、8番目はどうですか？
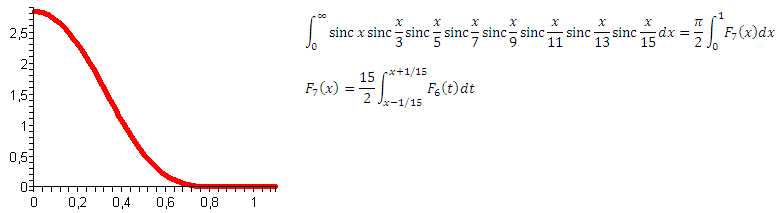
ストップストップストップ！ ここでは、CSIチームなしではできません！
機能がユニットに流れました！ 積分F 7 （x）はまだ1に等しいですが、これは0から∞を積分する場合です。 そして、団結して統合します！ これまで、xが1より大きい場合、すべての関数はゼロでしたが、遅かれ早かれ終了するはずです。
しかし、いつ終わりが来るのかを理解する方法は？ とても簡単です。 F 1 （x）はx <1/3で非ゼロでした。 F 2 （x）はそれを±1/5で平滑化しました。つまり、x <1/3 + 1/5で非ゼロでした。 同様に、これらすべての関数の非ゼロ値の境界を見つけることができ、 F 7 （x）の場合、この境界は初めて1を超えます。
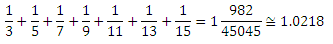
漏れた量を計算することさえ容易であり、それにより8番目の積分の正確な値を計算します。 境界F 1 （x）の左側には定数3があることに注意してください。F2 （x）は、この定数と係数5/2の積分、つまり係数3×5/2の直線を引いたものです。 境界1/3 + 1/5 + 1/7に十分に近いF 3 （x）は、その線と7/2の係数の積分、つまり次のようなものです。
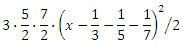。 同様の推論を続けて、境界の近傍でF 7 （x）の式を取得します。
実際、シフトして乗算された6度の通常の放物線。 1からボーダー1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 + 1/15に統合すると、ユニットの外部にリークした機能の数がわかります。 この問題は通常の分数で完全に解決できます。 それはいくらになるでしょう：
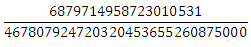
この数値を1から減算し、piを半分に乗算すると、8番目の積分の最終値が得られます。
このような積分は、それらを説明したデイビッドとジョナサンボルワインに敬意を表して、 ボルワイン積分と呼ばれます。 これらの素晴らしい積分の厳密な数学的証明（「良い関数」なし）およびその他の特性が必要な場合は、著者による記事を読んでください 。
結論：レベル80トローリング
これらの積分を開いたJonathan Borveinは、それらをMapleソフトウェアパッケージに導入し、 Mapleが8つの積分すべてを正しく処理することを確認して、開発者に「バグ」について通知しました。なに。 メープルの開発者の1人であるジャック・カレットは 、3日間3晩、ミスを求めて殺されました。 そして彼らは、数学者は退屈な人だと言う！