それでは始めましょう。 義務として、私は非線形ダイナミクス、ビデオ、画像処理を扱います。非線形ダイナミクスのかなり狭い部分、つまりローターの非線形振動も扱います。 ご存知のように、振動信号は時系列に過ぎず、信号は偏差の振幅の値です。たとえば、飛行機のタービンのローターなどです。 ご存知のように、この形式で表現できるのはローター振動だけではありません。 株価の変動、太陽の活動、その他の多くのプロセスは、時間内に配置された数字の単純なベクトルによって記述されます。 これらのプロセスはすべて1つの重要な要因によって結合されていることをさらに言います-それらは非線形であり、一部はカオス的です。これは、実際には、微分方程式の形でその運動の法則を正確に知っていても、システムの状態を任意の長い期間予測できないことを意味します。 そして最も重要なことは、ほとんどの場合、これらの方程式をなんらかの形で書くことさえできないということです。 そして、ここで実験と非線形ダイナミクスが助けになります。
非線形ダイナミクス
センサーから読み取り値を取得(通貨の引用を含むファイルをダウンロード)すると、出力に通常は複雑な形状の1次元信号があります。 信号が周期的であれば良いです。 そうでない場合は? さもなければ、我々は複雑なシステムを扱っており、さらにそれは非線形でカオス的な振動のモードにあるかもしれません。 この場合、複雑なシステムとは、多数の自由度を持つシステムを意味すると理解されています。 しかし、センサーから1次元の信号を取得します。 このシステムの他の自由度について知る方法は?
要点に移る前に、非線形ダイナミクスを分析する別の強力な方法に言及する価値があります。これは、時系列を分析する方法にスムーズに移行しました。 これは、1つの自由度のみからの信号によるシステム軌道のいわゆる復元です。 たとえば、ボールはスレッドの周りを円形に回転します。このプロセスを1つの平面で見ると、1つの軸からの信号しか発射できません。ボールは前後に走ります。 そして今、システム全体のN次元信号を完全に復元できることがわかりました。 しかし、完全ではありませんが、システムのトポロジ特性(つまり、そのジオメトリ)を保存するだけです。 この場合、ボールが周期的な軌道に沿って移動すると、復元された軌道は周期的になります。 メソッド自体は、単純な式に基づいています(2次元システムの場合)。
Y(i)= X(t)、Y1(i)= X(t + n)、nは時間遅延、Y、Y1は既に復元された信号です。 これは、テイケンスの定理で証明されています。 この例では、空間は2次元ですが、実際には、任意の多数の次元の空間にすることができます。 空間の次元を推定する方法は、このトピックのトピックには含まれていません。たとえば、偽の隣人の方法である可能性があることだけに言及します。
繰り返しプロット法
そのため、実際の物理システムのトポロジ特性が保存されているシステムの軌跡を取得しました。これは非常に重要です。 これで、パターンを識別するための画像認識方法の武器庫を設定できます。 しかし、それらのすべては、何らかの方法で、独自のコンピューティングの欠陥があるか、単に実装するのが困難です。 そして1987年に、エクマンと同僚は新しい方法を開発しました。その本質は次のように要約されます。 上記で取得した、次元Nのベクトルのセットである軌道は、次の式を使用して2次元平面にマッピングされます。
R [i、j、m、e] = O(e [i]、-|| S [i]-S [j] ||)ここで、i、jは平面上の点のインデックス、mは埋め込みスペースの次元、 O-ヘビサイド関数|| ... || -ノルムまたは距離(たとえば、ユークリッド)。 結果として視覚化されたマトリックスの外観は、もともと時系列として提示されたシステムのダイナミクスのアイデアを提供します。 上記のすべてを、太陽の活動を説明するウルフ数を使った実験の形で説明します(このシリーズの代わりに、通貨相場を簡単に取ることができます)。
結果
これは信号そのものです。
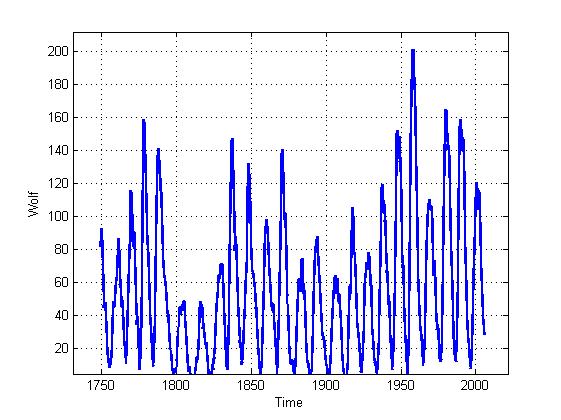
これは2次元空間で復元された軌道です(実際にはより多くの次元が含まれていますが、簡単にするために2次元空間を使用しますが、実践が示すように、定性的評価にはこれで十分です)
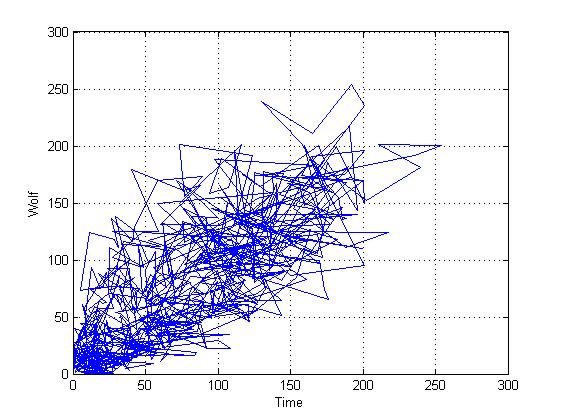
これは、いわゆる距離行列です(i番目の点からj番目の点までの距離という意味で)。 多くの場合、これらの図には、設計で使用(および使用)できる複雑な設計があります。

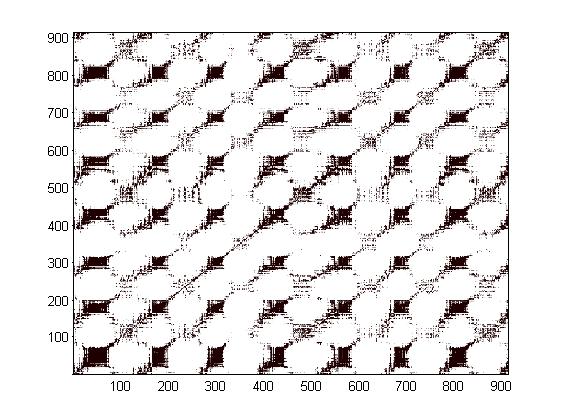
まあ、実際には再帰的なダイアグラム自体。 すべての分析方法を説明するには、このような図では不十分であり、400ページです。 定性分析に加えて、この方法では、ニューラルネットワークの場合に正常に使用できる定量的な指標も使用できます。 しかし、最も重要なことは、すでにこの図を簡単に確認しているということです。 まず、主対角線に垂直なバンドの存在は、システム内のカオス的または確率的プロセスの存在を示します(正確には、追加の研究が必要です)。 黒いドットで不均一に塗りつぶされたゾーンの存在は、不安定なプロセスを示しており、これらのプロセスの境界を時間内に正確に決定できます。
Matlabコード
clear; clc;
%
[X1,X2,X3,X4]=textread('data.txt','%f %f %f %f');
plot(X2,X4);grid;hold; ; ylabel('Wolf');xlabel('Time');
N = length(X1);
M = round(0.3*N);
M1 = N - M;
m = 2; %
t = 10; %
%
X(1,1) = 0;
X(1,2) = 0
j = 1;
%
for i=M1:(N - t)
X(j,1) = X3(i);
X(j,2) = X3(i + t);
j = j + 1;
end
figure;
plot(X(:,1),X(:,2));grid;hold; ; ylabel('Wolf');xlabel('Time');
N1 = length(X(:,1))
D1(1,1) = 0;
D2(1,1) = 0;
e = 30;
% RP -
for i = 1:N1
for j = 1:N1
D1(i,j)=sqrt((X(i,1)-X(j,1))^2+(X(i,2)-X(j,2))^2);
if D1(i,j) < e
D2(i,j) = 0;
else
D2(i,j) = 1;
end;
end;
end;
figure;
pcolor(D2) ;
shading interp;
colormap(pink);
figure;
pcolor(D1) ;
shading interp;
colormap(pink);
hold on
PS。 これは単なる基本的な例であり、もちろん、この方法の完全な能力をカバーするものではありません。 最も単純なケースでは、プロセスを自動化するために、平面上の図形を見つけるためのアルゴリズムを使用できます。 このようなシステムは、航空機のタービン監視システム、およびさまざまな金融プロセスの監視システムに関連する可能性があります。 このトピックの最も興味深い部分-これらの図の定量的指標の計算については触れませんでした。これについては、次のトピックで補正します。
文学
- J.-P. Ecmann N S. Oliffson KamphorstおよびD. Ruelle、動的システムの再発プロット
- www.recurrence-plot.tk
- en.wikipedia.org/wiki/Recurrence_plot