Clever Geek Handbook

通常の法則に従って分散された多次元データ配列をモデル化するアルゴリズム

既製のアルゴリズムを開発または研究する場合、多くの場合、作業の品質を判断する必要があります。 この目的のために実際のソースからのデータを使用することは常に可能とは限りません。なぜならそれらの特性はしばしば未知であり、したがって調査されたアルゴリズムの結果を予測することは不可能だからです。 この場合、データモデリングは、よく知られた分布則の1つに従って適用されます。 調査したアルゴリズムをモデルデータに適用すると、その実行結果がどうなるかを事前に予測できます。 満足できる結果が得られた場合は、実際のデータに適用してみてください。 当然、これはノンパラメトリックアルゴリズムにのみ適用されます。つまり、データ分布の法則とは無関係です。



最も一般的に使用されるモデリングデータは、通常の法則に従って配布されます。 残念ながら、MS Excelおよび一般的な統計パッケージ（SPSS、Statistica）では、1次元の統計分布のみをモデリングできます。 もちろん、多次元分布は、変数が独立している場合のみ、複数の1次元分布で構成できます。 互いに依存する変数を持つデータを調べる必要がある場合は、プログラムを作成する必要があります。



通常、多次元正規分布は 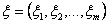数学的期待値のベクトルによって記述される 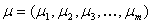および正定共分散行列 ：







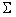どこで ;

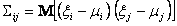i = 1,2,3、... m、j = 1,2,3、...、m;

mは、多次元の正規サンプルの特徴の数です。



ただし、共分散行列の代わりに、相関行列を使用する方が便利です。 および分散ベクトル 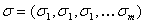、相関係数とは対照的に、相関係数は変数間の関連度を示すためです。 相関行列の形式は次のとおりです。









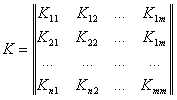
マトリックス係数の変換 行列係数へ 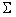次の式に従って発生します。











ベクトルをモデル化するには 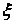線形ベクトル変換を使用できます そのコンポーネントは、ゼロに等しい数学的期待値パラメーターと1に等しい分散を持つ正規分布ランダム変数です（つまり、 ） Box-Muller変換など、1次元の正規確率変数をモデル化する方法は多数あります。2つの乱数を使用する そして 間隔（0; 1）に分布し、2つの数値が同時に取得され、パラメーターを使用して通常の法則に従って分布します ：















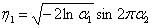
変換 で 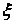式によって生成されます：











この変換では 行列から派生した下三角行列があります 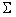コレスキー分解 ：











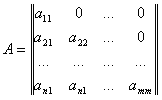
各行列要素 再帰的手順を使用して決定：











ここで、インデックスは範囲内で異なります 、および上限ゼロの礼拝堂との合計がゼロに等しい（つまり、 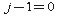それから 、 ）



説明した変換は、C ++の2つの関数の形式で実装できます。アルゴリズムを実装するメイン関数normal_model（）と、マトリックスの行列式を返す補助matrix_determinant（）です。



normal_model（）関数は、結果を持つマトリックスの次元から必要な変数と値の数を決定します。 成功した場合はtrue、失敗した場合はfalseを返します。 



//   ,    . //double MatrixMath [mq] -  .  //double MatrixDisp [mq] -   //vector<vector<double> > &correlation_matrix -   //vector<vector<double> > &MatrixRes -    bool normal_model (double MatrixMath[], double MatrixVar[], vector<vector<double> > &correlation_matrix, vector<vector<double> > &MatrixRes){ int mq =MatrixRes[0].size();//  int count=MatrixRes.size();//  double MatrixA[mq][mq]; //   A double MatrixN[count][mq]; //  ,       0, 1 int i,j,k; double suma, sumaa; double alfa1, alfa2; //.  ,    (0;1] vector<vector<double> > MatrixK(mq); //  K for (i=0;i<mq;i++){ MatrixK[i].resize(mq); } //     for (i=0; i<mq; i++){ for (j=0; j<mq; j++){ MatrixK[i][j]= correlation_matrix[i][j]* sqrt(MatrixVar[i]*MatrixVar[j]); } } if (matrix_determinant(MatrixK)<=0) return false; // .      ; //  A for (i=0; i<mq; i++){ for (j=0; j<=i; j++){ sumA=0; sumAA=0; for (k=0; k<j; k++){ sumA+= MatrixA[i][k] * MatrixA[j][k]; sumAA+= MatrixA[j][k] * MatrixA[j][k]; } MatrixA[i][j]=(MatrixK[i][j] - sumA)/ sqrt(MatrixK[j][j] - sumAA); } } //  ,       0, 1 srand(time(NULL)); for (i=0; i<count; i+=2){ for (j=0; j<mq; j++){ alfa1 = (double)rand()/(RAND_MAX+1.0); alfa2 = (double)rand()/(RAND_MAX+1.0); if (!alfa1 || !alfa2){ j--; }else{ MatrixN[i][j] = sqrt(-2*log(alfa1))*sin(2*M_PI*alfa2); if (i+1<count) MatrixN[i+1][j] = sqrt(-2*log(alfa1))*cos(2*M_PI*alfa2); } } } //   ,       0, 1      for (i=0; i<count; i++){ for (j=0; j<mq; j++){ MatrixRes[i][j]=MatrixMath[j]; for (k=0; k<mq; k++){ MatrixRes[i][j]+=MatrixA[j][k] * MatrixN[i][k]; } } } return true; } //    m  N x N double matrix_determinant (vector<vector<double> > & m){ double result=0; if (m.size()==1){ return m[0][0]; }else if(m.size()==2){ return m[0][0] * m[1][1] - m[0][1] * m[1][0]; }else if(m.size()==3){ return m[0][0] * m[1][1] * m[2][2] + m[0][1] * m[1][2] * m[2][0] + m[0][2] * m[1][0] * m[2][1] - m[2][0] * m[1][1] * m[0][2] - m[1][0] * m[0][1] * m[2][2] - m[0][0] * m[2][1] * m[1][2]; }else{ vector<vector<double> > m1(m.size()-1);// N-1 x N-1,     N-1 for (int i=0; i<m.size()-1; i++){ m1[i].resize(m.size()-1); } for (int i=0; i< m.size(); i++){ for (int j=1; j<m.size(); j++){ for (int k=0; k<m.size(); k++){ if (k<i){ m1[j-1][k] = m[j][k]; }else if(k>i){ m1[j-1][k-1] = m[j][k]; } } } result+= pow(-1,i) *m[0][i] * matrix_determinant(m1); } } return result; }


仕事の結果はここで見つけることができます 。 この関数には、fastcgiメカニズムを介してアクセスします。



使用された文献：

  1. Martyshenko C.N.、Martyshenko N.S.、Kustov D.A. 多次元データのモデリングとコンピューター実験。 エンジニアリングおよびテクノロジー、2007年-第2。 S. 47-52。
  2. Ermakov S.M.、Mikhailov G.A.、Statistical Modeling）、モスクワ：Nauka、1982年。
  3. V.フェラー、確率論とその応用の紹介、トランス。 英語から。、t。1-2、M.、1964-67。
  4. Rencher、Alvin C.（2002）、Method of Multivariate Analysis、第2版、John Wiley＆Sons。


More articles:


All Articles