- すべての興味深いアルゴリズムとその実装をC ++(C ++ 11標準)で共有します。
- このアルゴリズムに名前および/または正式な説明があるかどうかを調べます。
背景
それはすべて、Intelが開催したコンテストで始まりました。これについては、 投稿から学びました。 競争の本質は、2行で最大の長い共通部分文字列を見つける問題を解決するアルゴリズムを開発および実装することでした(ここでタスク全体を書き換えることは意味がないと思います)。 参照コードはその問題に添付されていました。 「等しくする」必要がある決定。 少し後に、このコンテスト専用のフォーラムから、参照コードはインテルのWebサイトで定式化された形式ではこの問題を解決しないことが明らかになりました。 つまり 競争の要点は次のとおりでした。「参照コードの出力を同じ入力パラメーターで正確に繰り返すプログラムを作成し、より高速かつ並列にするだけです」。
まあ、大丈夫、問題の説明と状況の不条理にもかかわらず、私はすぐに競争への参加をやめました。なぜなら、学生と卒業生だけがそこに参加できるからです。 サイトで説明されているタスク自体が好きでした。
問題の声明
このタスクの説明から理解した方法を次に示します。
S1とS2の 2つの行があり、最大の長い共通部分文字列(以降、必要な部分文字列-サブセットと呼びます)を見つける必要があります。その長さはM以上です。 結果としてその座標を導き出します。
座標は4つの整数です。
最初の2つは行S1に関連しています-これらは、見つかった部分文字列の最初と最後の文字の位置番号です。
2番目の2つの数値は同じ意味を持ち、2番目の行-S2にのみ適用されます。
たとえば、次の入力パラメーターがある場合:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
答えは次のとおりです。
0 3 5 8
(問題の元のステートメントでは、座標は1から表示する必要がありますが、これらはすでに結果の出力の詳細であり、アルゴリズム自体にはまったく適用されません)。
問題の要件は、アルゴリズムを並列化するために使用できるスレッドの数である追加の入力パラメーターKも示しています。
入り口で私たちに与えられたものを要約します:
- S1 、 S2-検索する2行。
- Mは、目的のサブストリングの可能な最小の長さです。
- Kは、並列化に使用できるスレッドの数です。
アルゴリズム
実際、ソリューションのアイデアは非常にシンプルで、3つのステップで構成されています。
- S1を最小の(長さM )セグメントに分割します。
- S2のプロジェクトセグメント。
- 取得した投影で、可能な限り長いサブセット(連続するセグメントの最大数から成る)を見つけます。
次の例のアルゴリズムの動作を検討してください。
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
K = 2
1)S1をそれぞれ長さM = 2のセグメントに分割します。
AB 、 BC 、 CC 、 CA
2)結果の各セグメントをS2に投影します。

またはオフセットの形式で:

したがって、 S1からS2への投影を取得します。

これから、この投影法を交差点マップと呼びます。
実際、交差マップは、長さがMであるすべてのセグメントの座標行列です。 つまり 各行列要素は行S2の座標を特徴づけ、一方、行列の行番号は行S1の座標を特徴づけます。 交差点マップを自由に使用できるので、すべての交差点(サブセット)を見つけて、それらから最大のものを選択できます。
3)最大サブセット(セグメントのセット)を検索します。
シンボリック形式で交差点マップを見ると、すでに視覚的に最も長いサブセットを見つけることができます:
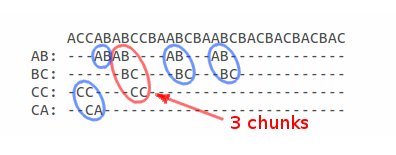
各セグメントがサブセットの始まりとして機能できることを考慮すると、交差マップを使用して、すべてのサブセットの長さを計算できます。サブセットの始まりは、この投影を構成するセグメントです。
次の図は、サブセットの長さを計算する方法を示しています。サブセットの開始は、座標5のセグメントです。

つまり 座標5から始まるサブセットの最大長はlen = 4です。座標3から始まるサブセットの場合、長さは2などになります。
同様に、交差マップの各セグメントを実行すると、最大の長いサブセットは、それぞれ行S1とS2の座標を持つ0と5の長さ4のサブセットであることがわかります。
並列化
ご覧のとおり、この問題を解決するためのすべてのステップ(ステップ1、2、3)は簡単に並列化でき、Map-Reduceが可能です。
1、2)各スレッドには独自のセグメント(または複数のセグメント)が割り当てられ、セグメントの投影を構築します。 全体として、すべてのセグメントに対して対応する投影が取得された後、既成の交差マップが取得されます。

3.1)各スレッドには、独自のシリアル番号(n)が割り当てられます。 次に、n番目の位置から始まるn番目のストリームが、交差点マップの各K番目の要素を処理します。 したがって、交差マップをいくつかの(フローの数)部分に分割します。 上記のように、これらのパーツのうち、最大のサブセットが選択されます。
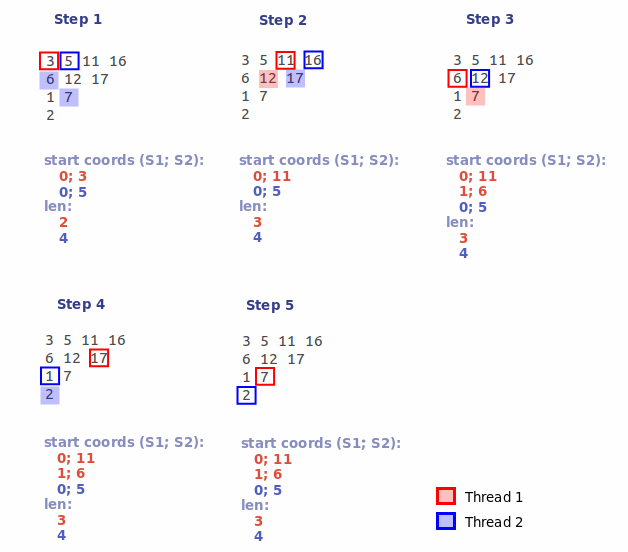
3.2)すべてのスレッドが完了した後、サブセットのいくつかのグループを取得します。 取得したグループから、最大セグメント長を持つグループを選択します。 この例では、2つのグループがあります。長さ3文字のセグメントを含むストリーム#1によって形成されるグループ(初期座標: 0; 11 and 1; 6 )、および長さ4文字のセグメントを含むストリーム#2によって形成されるグループ(座標0; 5を使用)。 2番目のグループのセグメント長が最も長いため、最初のグループはすぐに破棄されます。
その結果、サブセットの初期座標( 0; 5 )を取得し、その長さは4です。 最終的な座標を見つけるには、次の式を使用します:end_coord = start_coord + len-1。
したがって、答えは0 3 5 8になります。
おわりに
C ++でのこのアルゴリズムの実装の詳細については触れないことにしました。これは既にこの記事の範囲を超えているからです。 このアルゴリズムのC ++(C ++ 11)の実装については、GCCでコンパイルするために、 -pthreadおよび-std = c ++ 0Xフラグを設定することを忘れないでください。
質問
このアルゴリズムは、問題の明らかな解決策として思い浮かびましたが、正式な名前や正式な説明があるかどうかわかりませんか?