互いに素な数p 1 、... p nのシステムでは、範囲[0; M)、ここでM = p 1 * p 2 * ... * p nは 、ベクトル(a 1 、a 2 、...、a n )の形式で1対1で表現できます。ここで、 ai = X%p i (以下「%」) Xをp iで整数除算した余りを取得する操作)。
p 1 、... p n-システムモジュール
a 1 、a 2 、...、a n-与えられたモジュールシステムの数の剰余(控除)
一見、このようなシステムがどのような利点をもたらすかは明らかではありませんが、マイクロエレクトロニクスの一部の分野でモジュラー演算を効果的に使用できるようにする2つの特性があります。
- 加算および乗算の放電の転送の欠如。 相互に単純な数の体系(p 1 、p)に従って、残基の体系(x 11 、x 12 、...、x 1n )および(x 21 、x 22 、...、x 2n )として表される2つの数値X 1およびX 2を与えます2 、...、p n )。 この場合:
X 3 = X 1 + X 2 =((x 11 + x 21 )%p 1 、(x 12 + x 22 )%p 2 、...、(x 1n + x 2n )%p n )
X 4 = X 1 * X 2 =((x 11 * x 21 )%p 1 、(x 12 * x 22 )%p 2 、...、(x 1n * x 2n )%p n )
つまり、2つの数値を加算または乗算するには、ベクトルの対応する要素を加算または乗算するだけで十分です。これは、マイクロエレクトロニクスの場合、これを並列に実行でき、小さい次元p 1 、p 2 、...、p nにより非常に迅速に実行できることを意味します。 - ベクトルのある位置でのエラーは、ベクトルの他の位置での計算には影響しません。 位置番号システムとは対照的に、ベクトルのすべての要素は同等であり、そのうちの1つのエラーはダイナミックレンジの縮小につながります。 この事実により、フォールトトレランスとエラー修正を強化したデバイスを設計できます。
| 通常の乗算 | モジュラー乗算 |
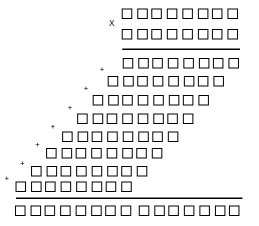 |  |
しかし、すべてが私たちが望むほどスムーズではありません。 位置番号システムとは異なり、次の操作(「非モジュラー」と呼ばれる)は位置番号システムよりも複雑です:数値の比較、オーバーフロー制御、除算、平方根など。 マイクロエレクトロニクスでモジュラー演算を使用する最初の成功した試みは1950年代にさかのぼりますが、非モジュラー操作の難しさにより、関心はやや落ち着きました。 ただし、現在、モジュラー演算は次の理由で再びマイクロエレクトロニクスに戻っています。
- 低消費電力で高速が必要なモバイルプロセッサの普及。 算術加算/乗算演算で転送が行われないため、エネルギー消費が削減されます。
- チップ上の要素の密度が高くなると完全なテストができない場合があるため、エラーの可能性に対するプロセッサの安定性の重要性が高まっています。
- 高速性を必要とし、主に数値の加算と乗算を含む、ベクトルに対する多数の演算を備えた特殊なプロセッサの出現(例として、行列乗算、ベクトルのスカラー積、フーリエ変換など)。
現在、モジュラー演算は、デジタル信号処理、暗号化、画像処理/オーディオ/ビデオなどの分野で使用されています。
直接変換
位置番号システム(通常はバイナリ形式)から残差の番号システムへの直接変換は、システムの各モジュールの除算の剰余を見つけることにあります。
例 :モジュールのシステム(3、5、7)から数値X = 25の表現を検索するとします。 X =(25%3、25%5、25%7)=(1、0、4)。
特定のモジュールのマイクロエレクトロニクスで残留物を見つける実装は、残留物の次の特性に基づいています。
(a + b)%p =(a%p + b%p)%p
(a * b)%p =(a%p * b%p)%p
X%p =(x n-1 * 2 n-1 + x n-2 * 2 n-2 + x 0 * 2 0 )%p =((x n-1 )%p * 2 n-1 %p)+((x n-2 )%p * 2 n-2 %p)+ ... + x 0 %p)%p。 この場合、x n-1 、... x 0は実際には0または1であるため、(2 i %p)という形式の剰余を追加する必要があります。
例 :25を指定するか、2進数システム11001で、7を法とする剰余を求めます。
25%7 =(1 * 2 4 + 1 * 2 3 + 0 * 2 2 + 0 * 1 + 1 * 2 0 )%7 =(2 4 %7 + 2 3 %7 + 1%7)%7 = (2 + 1 + 1)%7 = 4
使用されるモジュールのシステムは、特定のタスクに対して選択されます。 たとえば、32ビットの数値を表すには、次のモジュールシステムで十分です。(7、11、13、17、19、23、29、31)-それらはすべて相互に単純で、製品は6685349671> 4294967296です。各モジュールはつまり、加算と乗算の演算は5ビットの数値に対して実行されます。
特に重要なのは、次の形式のモジュールシステムです:(2 n -1、2 n 、2 n +1)それらの直接および逆変換が最も簡単な方法で実行されるという事実のため。 2 nで割った余りを取得するには、数値のバイナリ表現の最後のn桁を取得するだけで十分です。
算術演算
例 :モジュールのシステム(3、5、7)を指定します。つまり、結果が3 * 5 * 7 = 105を超えない操作を実行できます。2つの数字8と10を掛けます。
8 =(8%3、8%5、8%7)=(2、3、1)
10 =(10%3、10%5、10%7)=(1、0、3)
8 * 10 =((2 * 1)%3、(3 * 0)%5、(1 * 3)%7)=(2、0、3)
確認する
80 =(80%3、80%5、80%7)=(2、0、3)
逆変換
残差クラスの番号システムから位置番号システムへの逆変換は、次の2つの方法のいずれかで実行されます。
- 中国の剰余定理または直交基底のシステムに基づく
- ポリアディックコードに基づく(他の名前は混合基数システム、混合ベースシステム)
実際、さまざまな文献で提案されている残りの方法は、これら2つの方法の混合物です。
中国の剰余定理に基づく方法は、次の考え方に基づいています。
X =(x 1 、x 2 、... x n )=(x 1、0、...、0)+(0、x 2 、...、0)+ ... +(0、0、...、x n )= x 1 *(1、0、...、0)+ x 2 *(0、1、...、0)+ ... + x n *(0、0、...、1)。
つまり、逆変換の場合、直交基底B1 =(1、0、...、0)、B2 =(0、1、...、0)、...、BN =(0、0、...、1)のシステムを見つける必要があります。 これらのベクトルは、与えられた基底に対して一度見つけられ、それらの検索のために、次の形式の方程式を解く必要があります:(M i * b i )%p i = 1、ここでM i = M / p iおよびb iは所望の数です。 この場合、位置表現B i = M i * b iおよび
X =(x 1 *(M 1 * b 1 )+ x 2 *(M 2 * b 2 )+ ... + x n *(M n * b n ))%M
例 :モジュールのシステム(3、5、7)が与えられると、M iとb iの値が見つかります(0 <i <= 3)
M = 3 * 5 * 7 = 105
M 1 = 105/3 = 35
M 2 = 105/5 = 21
M 3 = 105/7 = 15
(35 * b 1 )%3 = 1 => b 1 = 2
(21 * b 2 )%5 = 1 => b 2 = 1
(15 * b 3 )%7 = 1 => b 3 = 1
次に、残差クラスのシステムでいくつかの数を変換します。 置く
X =(2、3、1)=(2 * 35 * 2 + 3 * 21 * 1 + 1 * 15 * 1)%105 =(140 + 63 + 15)%105 = 218%105 = 8
この方法の欠点は、逆変換が大きな数(M 1 、...、M n )の乗算と加算、および大きな数Mを法とする剰余を取る操作を必要とすることです。
ポリアディックコードに基づく方法は、任意の数Xを[4]のように互いに素な数p 1 、... p nのシステムで表現できるという考えに基づいています。
X = a 1 + a 2 * p 1 + a 3 * p 1 * p 2 + ... + a n-1 * p 1 * p 2 * ... * p n-2 + a n * p 1 * p 2 * ... * p n-1 、ここで0 <a i <p i
- X%p 1 = x 1 = a 1
- (X-a 1 )%p 2 =(x 2 -a 1 )%p 2 =(a 2 * p 1 )%p 2 => a 2 =((p 1 -1 )%p 2 *(x 2 -a 1 ))%p 2
- (X-a 1 -a 2 * p 1 )%p 3 =(a 3 * p 1 * p 2 )%p 3 => a 3 =((p 2 -1 )%p 3 *((p 1- 1 )%p 3 *(x 3 -a 1 )-a 2 ))%p 3
- ...
この方法を使用するには、(p i -1 )%p k -1の形式の定数が必要です。 また、 1の値が表示されるとすぐに3の計算を開始できることに気付くことができます。 コンベアコンバーターは、この方法に基づいて構築できます。
例 :同じ例を考えてみましょう-モジュールシステム(3、5、7)で数値X =(2、3、1)の位置表現を見つけます
- a 1 = x 1 = 2
- a 2 =((p 1 -1 )%p 2 *(x 2 -a 1 ))%p 2 =((3 -1 )%5 *(3-2))%5 = 2 * 1 = 2
- a 3 =((p 2 -1 )%p 3 *((p 1 -1 )%p 3 *(x 3 -a 1 )-a 2 ))%p 3 =((5 -1 )%7 * ((3 -1 )%7 *(1-2)-2))%7 =(3 *(5 *(1-2)-2))%7 =(3 *(-7))%7 = 0
- X = a 1 + a 2 * p 1 + a 3 * p 1 * p 2 = a 1 + 3 * a 2 + 15 * a 3 = 2 + 3 * 2 + 15 * 0 = 8
注 :(3 -1 )%5の形式の定数を見つけるには、方程式(3 * x)%5 = 1を解く必要があります。ここで、0 <= x <5
PS
トピックが十分に大きく、すべてを1つの記事に収めることができないため、この記事はやや面倒です。 次の記事では、モジュラー算術のさまざまな側面をより詳細に説明しようとします。 Habrでは、このトピックに関連するものはまったく見つけられませんでした。他の記事の簡単なリファレンスだけを見つけたので、簡単な例を使って短いレビューを書くことにしました。 このトピックに興味がある人は、参考文献のリスト(英語)から本番号[3]を読むことをお勧めします。多くの例を含むアクセス可能な言語で書かれています。
文学
[1] en.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0% B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81% D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
[2] en.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1% 82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0% D1%82%D0%BA%D0%B0%D1%85
[3] Amos Omondi、Benjamin Premkumar、Residue Number Systems:Theory and Implementation、2007。
[4] MAソダーストランド、WKジェンキンス、ジョージアジュリエン、FJテイラー。 1986.剰余数システム算術:デジタル信号処理の最新アプリケーション、IEEE Press、ニューヨーク。