私たちのほとんどは、何らかの方法で文字列を操作します。 これを避けることはできません-コードを書くと、毎日行を折りたたみ、コンポーネントに分割し、インデックスで個々の文字を参照する運命にあります。 私たちは、文字列が固定長の文字の配列であるという事実に長い間慣れ親しんでおり、これには、文字列の操作に対応する制限が伴います。
そのため、2行をすばやく結合することはできません。そのためには、まず必要な量のメモリを割り当ててから、そこに連結された行からデータをコピーする必要があります。 明らかに、このような操作にはO(n)のオーダーの複雑さがあります。ここで、nは行の全長です。
それがコードです
string s = ""; for (int i = 0; i < 100000; i++) s += "a";
とてもゆっくり働きます。
巨大な文字列をすばやく連結したいですか? 文字列がストレージに連続したメモリ領域を必要とするという事実が気に入らないのですか? バッファを使用して文字列を作成するのにうんざりしていませんか?
私たちを救うデータ構造は、 ロープ文字列 、または「ロープ文字列」と呼ばれます。 その動作の原理は非常に単純であり、直感的な考慮事項から文字通り推測することができます。
アイデア
2行追加する必要があるとします。
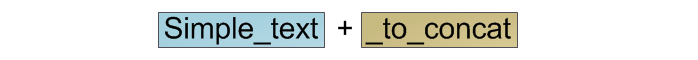
古典的な行の場合、必要なサイズのメモリ領域を選択し、最初の行の内容を最初に、2番目の行の内容を最後にコピーします。
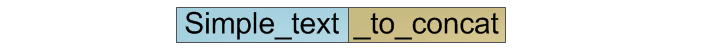
上記のように、この操作の複雑さはO(n)です。
しかし、結果の文字列が2つのソース文字列の連結であるという情報を使用するとどうなりますか? 実際、文字列インターフェイスを提供し、そのコンポーネントに関する情報を保存するオブジェクトを作成します-ソース文字列:

この文字列の結合方法はO(1)で機能します-ソース文字列のラッパーオブジェクトを作成するだけです。 このオブジェクトも文字列であるため、他の文字列と組み合わせて、必要な連結を取得できます。
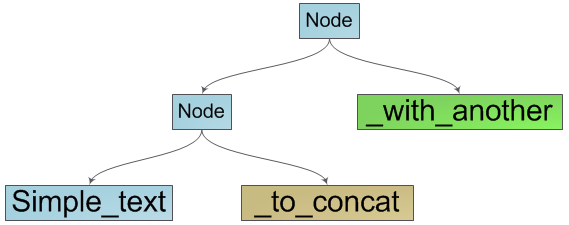
私たちの構造が二分探索木であり、その葉が私たちの行の基本的な構成要素である文字群であることはすでに明らかです。 また、文字列の文字を列挙する方法も明らかになります。これは、ツリーの葉の文字の順次列挙によるツリーの深さのトラバースです。
索引付け
ここで、インデックスによって文字列文字を取得する操作を実装します。 これを行うために、ツリーのノードに重みという追加の特性を導入します。 シンボルの一部がツリーノード(ノード-リーフ)に直接格納されている場合、その重みはこれらのシンボルの数に等しくなります。 それ以外の場合、ノードの重みはその子孫の重みの合計に等しくなります。 つまり、ノードの重みは、それが表す文字列の長さです。
Nodeノードで表される文字列のi番目の文字を取得する必要があります。 その後、2つのケースが発生する可能性があります。
- ノード-シート。 その後、データが直接含まれ、「内部」文字列のi番目の文字を返すだけで十分です。
- ノードは複合です。 次に、ノードのどの子孫が検索を続行する必要があるかを見つける必要があります。 左の子の重みがiより大きい場合-求められている文字は左の部分文字列のi番目の文字です。それ以外の場合、右の部分文字列の(iw)番目の文字です。wは左の部分木の重みです。
これで、O(1)の文字列を連結し、O(h)(ツリーの高さ)の文字列にインデックスを付けることができます。 しかし、完全に幸福にするためには、2行に分割し、部分文字列を削除して挿入する操作をすばやく実行する方法を学ぶ必要があります。
解散
したがって、文字列があり、その位置kのいくつかで2つの部分文字列に分割することが非常に必要です(図の数字は、対応するツリーのサイズです)。
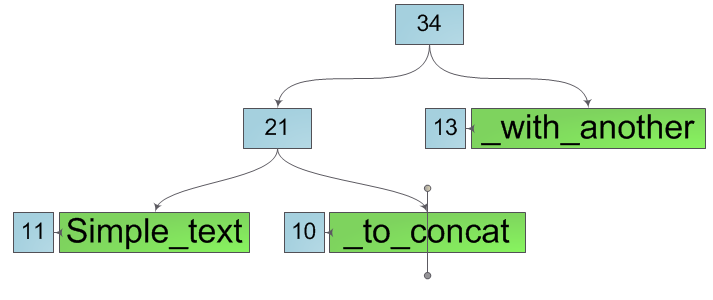
「改行」の場所は、常にツリーの葉の1つにあります。 このシートを、元のシートのサブストリングを含む2つの新しいシートに分割します。 さらに、この操作では、シートの内容を新しいものにコピーする必要はありません。オフセットや長さなどのシートの特性を入力し、新しいシートの元の文字の配列へのポインターを保存します。
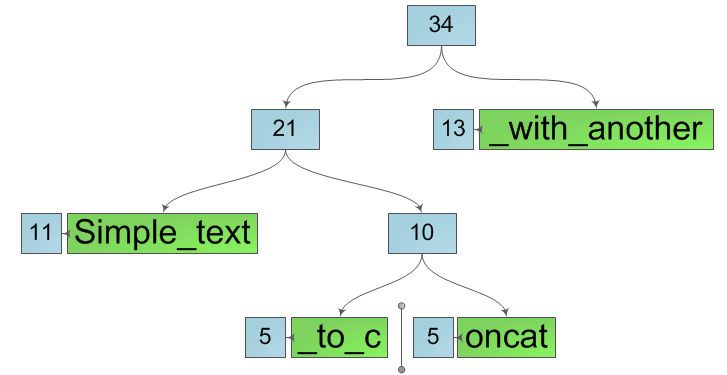
次に、リーフからルートまでのパスに沿ってすべてのノードを分割し、代わりに、作成される左右の部分文字列にそれぞれ属するノードのペアを作成します。 また、現在のノードを変更するのではなく、新しいノードを2つだけ作成します。 これは、行分割操作が元のサブストリングに影響を与えることなく新しいサブストリングを生成することを意味します。 元の行を分割した後、次の図のように2つの新しい行を取得します。

そのような線の内部構造が最適ではないことに気付くのは簡単です-明らかに余分なものもあります。 ただし、この迷惑な省略を修正するのは簡単です。両方の部分文字列のカットからルートまで歩いて、ちょうど1つの子孫を持つ各ノードをこの同じ子孫に置き換えるだけで十分です。 その後、すべての余分なノードが消え、最終的な形式で必要なサブストリングが取得されます。

文字列分割操作の複雑さは明らかにO(h)です。
削除して貼り付け
すでに実装されている分割およびマージ操作のおかげで、削除と挿入は基本的な方法で行われます-部分文字列を削除するには、削除されたセクションの最初と最後でソース行を分割し、最後の行を接着します。 特定の位置の行に挿入するには、元の行をその中の2つの部分文字列に分割し、挿入したものと目的の順序で接着します。 どちらの操作にもO(h)の漸近的な動作があります。
最適化
バランス調整
「木」という言葉を聞いた熱心な読者は、必然的に他の2つ、「対数」と「バランス」を思い出すでしょう。 そして、いつものように、切望された対数漸近を達成するためには、私たちのツリーのバランスをとる必要があります。 実際、文字列をマージする現在の方法では、ツリーの内部構造は、たとえば次の図のように「はしご」のように見えます。
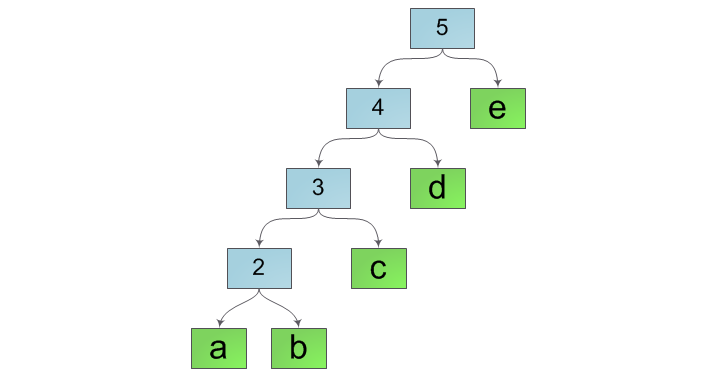
これを回避するために、行の各組み合わせで結果のバランスを確認し、必要に応じてツリー全体を再構築してバランスを取ります。 バランスの良い条件は、文字列の長さが少なくともフィボナッチ数の(h + 2)でなければならないことです。 この状態の理論的根拠と接着操作に対するいくつかの追加修正は、Bohem、Atkinson、およびPlassの「 Ropes:an Alternative Alternative to Strings」で与えられました。
細い線の直接連結
ツリーノードをメモリに保存することはまったく無料ではありません。 行に1つの文字を追加すると、ツリーノードに関する情報の保存に、行の文字自体よりも1桁多くのメモリが費やされます。 このような状況を回避し、ツリーの高さを減らすために、「クラシック」な方法で特定の長さ(たとえば32)より短い行を接着することをお勧めします。 これによりメモリが大幅に節約され、全体的なパフォーマンスにもほとんど影響しません。
最終位置キャッシング
ほとんどの場合、文字列の文字を順番に繰り返し処理します。 この場合、インデックスiおよびi + 1でシンボルを要求すると、それらが物理的に木の同じ葉にある可能性が非常に高くなります。 これは、これらの文字を検索するときに、ツリーのルートからリーフまで同じパスを繰り返すことを意味します。 この問題の明らかな解決策はキャッシュです。 これを行うには、次の文字を検索するときに、それが配置されているシートと、このシート自体に含まれるインデックスの範囲を覚えておいてください。 次に、次の文字を検索するとき、最初にインデックスが保存された範囲にあるかどうかを確認し、そうであれば、保存されたシートで直接検索します。 最後の1つの位置ではなく、たとえば循環リスト内のいくつかの位置を記憶して、さらに先へ進むこともできます。
以前の最適化と合わせて、この手法を使用すると、インデックスの漸近性をO(ln(n))からほぼO(1)に改善できます。
まとめ
結果として何が得られますか? 挿入、削除、連結(古典的な文字列のO(n)ではなく)の対数漸近的な振る舞いと、ほぼO(1)のインデックス付けを行う、ストレージに連続したメモリ領域を必要としない永続的な文字列実装を取得します。
最後に、英語のウィキの記事 、Java実装 、SGI WebサイトのC ++実装の説明など、便利なリンクをいくつか紹介します 。
ロープを使って、ルカ!