今日は、ロスレスデータ圧縮のトピックに触れたいと思います。 ハブには特定のアルゴリズムに特化した記事が既にあるという事実にもかかわらず、私はこれについてもう少し詳しく話したいと思いました。
誰もが自分にとって興味深いものを見つけることができるように、数学的な説明と通常の方法で説明の両方を提供しようとします。
この記事では、圧縮の基本的な瞬間とアルゴリズムの主要なタイプに触れます。
圧縮 最近必要ですか？
はい、もちろんです。 もちろん、大容量の記憶媒体と高速データ伝送チャネルの両方にアクセスできるようになったことは誰もが理解しています。 ただし、同時に、送信される情報の量も増えています。 数年前に1枚のディスクに収まる700メガバイトの映画を見ていた場合、今日ではHD品質の映画が数十ギガバイトを占めることがあります。
もちろん、すべてを圧縮することの利点はすべてではありません。 ただし、必要でない場合でも、圧縮が非常に役立つ状況があります。
- ドキュメントの電子メール送信（特にモバイルデバイスを使用した大量のドキュメント）
- ウェブサイトでドキュメントを公開するとき、トラフィックを節約する必要性
- ストレージの変更または追加が困難な場合は、ディスク容量を節約してください。 たとえば、これは設備投資の予算を得ることが容易ではなく、十分なディスク容量がない場合に発生します。
もちろん、圧縮が役立つさまざまな状況を思いつくことができますが、これらのいくつかの例で十分です。
すべての圧縮方法は、非可逆圧縮と非可逆圧縮の2つの大きなグループに分けることができます。 ロスレス圧縮は、情報をビット単位で正確に復元する必要がある場合に使用されます。 このアプローチは、たとえばテキストデータを圧縮する場合に唯一可能なアプローチです。
ただし、場合によっては、正確な情報の回復は不要であり、非可逆圧縮とは異なり、通常は実装が簡単で高度なアーカイブを提供する非可逆圧縮を実装するアルゴリズムを使用できます。
| 非可逆圧縮 |
| 「十分な」データ品質を維持しながら、最高の圧縮率。 これらは主に、アナログデータ（音声、画像）の圧縮に使用されます。 このような場合、解凍されたファイルはビット単位の比較レベルで元のファイルと大きく異なる可能性がありますが、ほとんどの実際のアプリケーションでは人間の耳や目とは事実上区別できません。 |
| ロスレス圧縮 |
| データはビット単位で正確に復元されるため、情報が失われることはありません。 ただし、ロスレス圧縮は通常、最悪の圧縮率を示します。 |
それでは、ロスレス圧縮アルゴリズムに移りましょう。
ユニバーサルロスレス圧縮方法
一般的な場合、圧縮アルゴリズムが構築される3つの基本的なオプションがあります。
メソッドの最初のグループはストリーム変換です。 これは、処理済みの新しい着信非圧縮データの説明を意味します。 この場合、確率は計算されません。文字エンコードは、LZメソッド（Abraham LempelとJacob Zivaにちなんで名付けられた）などですでに処理されたデータに基づいてのみ実行されます。 この場合、エンコーダーに既に知られている特定の部分文字列の2番目以降の出現は、その最初の出現への参照に置き換えられます。
方法の2番目のグループは、統計的圧縮方法です。 順番に、これらの方法は適応（またはフロー）とブロックに分けられます。
最初の（適応）バージョンでは、新しいデータの確率の計算は、エンコード中にすでに処理されたデータに基づいています。 これらの方法には、ハフマンアルゴリズムとシャノンファノアルゴリズムの適応バージョンが含まれます。
2番目（ブロック）の場合、各データブロックの統計は個別に計算され、最も圧縮されたブロックに追加されます。 これらには、Huffman、Shannon-Fano、算術コーディング法の静的バージョンが含まれます。
3番目のグループのメソッドは、いわゆるブロック変換メソッドです。 受信データはブロックに分割され、ブロック全体が変換されます。 同時に、特にブロックの順列に基づく一部の方法では、データ量が大幅に（またはまったく）減少しない場合があります。 ただし、このような処理の後、データ構造は大幅に改善され、他のアルゴリズムによるその後の圧縮はより成功し、高速になります。
データ圧縮の基礎となる一般原則
すべてのデータ圧縮方法は、単純な論理原理に基づいています。 最も頻繁に発生する要素はより短いコードでエンコードされ、より頻繁に発生しない要素はより長いコードでエンコードされると想像すると、すべての要素が同じ長さのコードで表される場合よりも、すべてのデータを保存するスペースが少なくなります
要素の出現頻度とコードの最適な長さとの正確な関係は、いわゆるシャノンのソースコーディング定理に記述されています。これは、最大無損失圧縮限界とシャノンエントロピーを決定します。
ちょっとした数学
要素s iの発生確率がp（s i ）に等しい場合、この要素-log 2 p（s i ）ビットを表すことが最も有利です。 エンコード中にすべての要素の長さをlog 2 p（s i ）ビットに減らすことができる場合、エンコードされたシーケンス全体の長さは、考えられるすべてのエンコード方法で最小になります。 さらに、すべての要素の確率分布F = {p（s i ）}が一定で、要素の確率が相互に独立している場合、コードの平均長さは次のように計算できます。
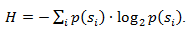
この値は、確率分布Fのエントロピー、または特定の時点でのソースのエントロピーと呼ばれます。
ただし、通常、要素の出現確率は独立ではなく、いくつかの要因に依存します。 この場合、新しいエンコードされた要素s iごとに、確率分布Fは値F kを取ります。つまり、各要素F = F kおよびH = H kです。
言い換えれば、ソースは状態kにあり、すべての要素s iの確率p k （s i ）の特定のセットに対応しています。
したがって、この修正が行われると、平均コード長は次のように表現できます。
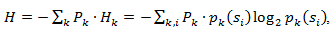
ここで、P kは状態kのソースを見つける確率です。
そのため、この段階では、圧縮は頻繁に発生する要素を短いコードに、またはその逆に置き換えることに基づいており、コードの平均長を決定する方法も知っています。 しかし、コード、コーディング、およびそれはどのように起こるのでしょうか？
メモリレスエンコーディング
メモリなしのコードは、データを圧縮できる最も単純なコードです。 メモリレスコードでは、エンコードされたデータベクトルの各文字は、バイナリシーケンスまたは単語のプレフィックスセットのコードワードに置き換えられます。
私の意見では、最も明確な定義ではありません。 このトピックをより詳細に検討してください。
アルファベットを与えましょう
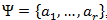いくつかの（有限の）文字で構成されます。 このアルファベット（A = a 1 、a 2 、...、a n ）からの文字の各有限シーケンスをwordと呼び、数字nはこのワードの長さと呼びます。
また、別のアルファベットを与えましょう
。 同様に、このアルファベットの単語をBとして指定します。
アルファベットのすべての空でない単語のセットにさらに2つの表記を導入します。 させて
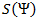-最初のアルファベットの空でない単語の数、および 
-2番目。
また、最初のアルファベットの各単語Aに2番目のアルファベットの単語B = F（A）を関連付けるマッピングFを指定します。 次に、単語Bは単語Aのコードと呼ばれ、元の単語からそのコードへの遷移はコーディングと呼ばれます。
単語は1文字で構成することもできるため、最初のアルファベットの文字と2番目のアルファベットの対応する単語の対応を特定できます。
a 1 <-> B 1
a 2 <-> B 2
...
a n <-> B n
この対応は回路と呼ばれ、byで示されます。
この場合、単語B 1 、B 2 、...、B nは基本コードと呼ばれ、それらの助けを借りたエンコーディングのタイプはアルファベットエンコーディングと呼ばれます 。 もちろん、私が上で説明したことをすべて知らなくても、私たちのほとんどはこのタイプのコーディングに出くわしました。
そこで、 アルファベット、単語、コード、 コーディングの概念を決定しました。 ここで、 プレフィックスの概念を紹介します 。
単語Bの形式をB = B'B ''とします。 次に、B は単語Bの先頭または接頭辞と呼ばれ、Bはその末尾です。 これはかなり単純な定義ですが、単語Bについては、特定の空の単語ʌ（「スペース」）と単語B自体の両方が開始と終了の両方と見なされることに注意してください。
したがって、メモリのないコードの定義を理解することに近づきます。 理解する必要がある最後の定義は、プレフィックスセットです。 スキームAには、1≤i、j≤r、i≠jの場合、単語B iが単語B jの接頭辞ではない場合、接頭辞のプロパティがあります。
簡単に言えば、プレフィックスセットは、他の要素のプレフィックス（または先頭）である要素がない有限セットです。 このようなセットの簡単な例は、たとえば通常のアルファベットです。
そこで、基本的な定義を見つけました。 では、メモリレスコーディング自体はどのように発生しますか？
3段階で発生します。
- 元のメッセージの文字のアルファベットΨがコンパイルされ、アルファベット文字はメッセージ内での出現確率の降順にソートされます。
- アルファベットΨの各シンボルa iは、プレフィックスセットΩの特定の単語B iに関連付けられています。
- 各文字はエンコードされ、その後に1つのデータストリームのコードの組み合わせが続きます。これは圧縮の結果です。
この方法を説明する標準的なアルゴリズムの1つは、ハフマンアルゴリズムです。
ハフマンアルゴリズム
ハフマンアルゴリズムは、入力データブロック内の同じバイトの出現頻度を使用し、短い長さのビットチェーンの頻繁なブロックと一致します。 このコードは最小限の冗長性です。 入力ストリームに関係なく、出力ストリームのアルファベットがゼロと1文字の2文字のみで構成されている場合を考えます。
まず、ハフマンアルゴリズムでコーディングする場合、回路constructを構築する必要があります。 これは次のように行われます。
- 入力アルファベットのすべての文字は、確率の降順で並べられます。 出力ストリームのアルファベットからのすべての単語（つまり、エンコードするもの）は最初は空と見なされます（出力ストリームのアルファベットはシンボル{0,1}のみで構成されていることを思い出します）。
- 発生確率が最も低い入力ストリームの2つのシンボルa j-1およびa jは、確率pが含まれるシンボルの確率の合計に等しい1つの「擬似シンボル」に結合されます。 次に、単語B j-1の先頭に0を追加し、単語B jの先頭に1を追加します。これは、それぞれ文字コードa j-1およびa jになります。
- これらの文字を元のメッセージのアルファベットから削除しますが、生成された擬似シンボルをこのアルファベットに追加します（当然、確率を考慮して、正しい場所でアルファベットに挿入する必要があります）。
アルファベットのすべての元の文字を含むアルファベットに擬似文字が1つだけ残るまで、手順2と3を繰り返します。 さらに、各ステップおよび各文字で、対応する単語B iが（1または0を追加することにより）変化するため、この手順が完了すると、アルファベットa iの各初期文字は特定のコードB iに対応します。
より良い説明のために、小さな例を考えてみましょう。
4つの文字（{a 1 、a 2 、a 3 、a 4 }）のみで構成されるアルファベットがあるとします。 また、これらのシンボルの発生確率はそれぞれ等しいと仮定します。p1 = 0.5; p 2 = 0.24; p 3 = 0.15; p 4 = 0.11（すべての確率の合計は明らかに1に等しい）。
したがって、このアルファベットの回路を構築します。
- 確率が最も低い2つの文字（0.11と0.15）をp '擬似文字に結合します。
- 結合された文字を削除し、結果の擬似文字をアルファベットに挿入します。
- 最小確率（0.24および0.26）の2つの文字をp ''擬似文字に結合します。
- 結合された文字を削除し、結果の擬似文字をアルファベットに挿入します。
- 最後に、残りの2文字を組み合わせて、ツリーの最上部を取得します。
このプロセスを説明すると、次のようなものが得られます。
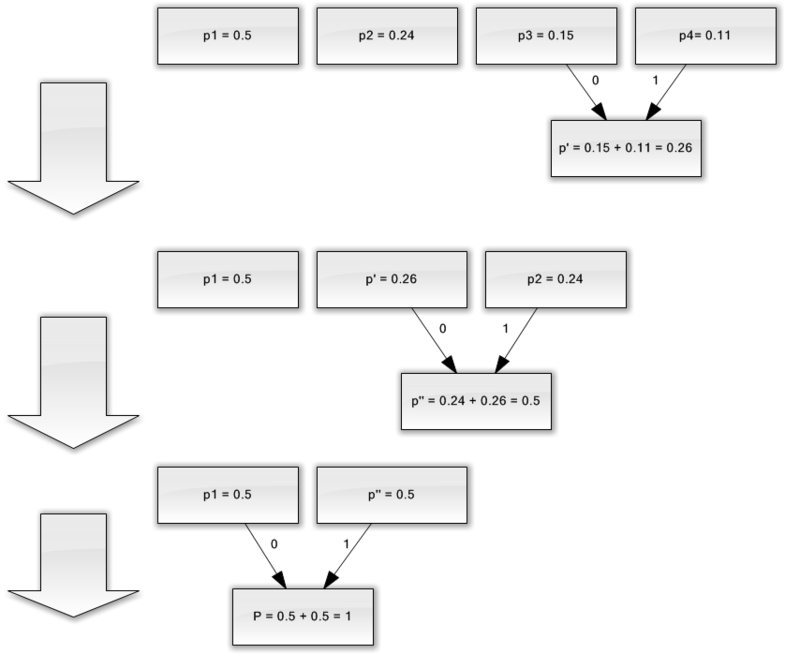
ご覧のとおり、各マージで、コード0と1をマージする文字に割り当てます。
したがって、ツリーが構築されると、各文字のコードを簡単に取得できます。 この場合、コードは次のようになります。
1 = 0
a 2 = 11
3 = 100
a 4 = 101
これらのコードはいずれも他のコードのプレフィックスではないため（つまり、悪名高いプレフィックスセットを取得したため）、出力ストリーム内の各コードを一意に識別できます。
そのため、最も頻繁に使用される文字は最短のコードでエンコードされ、その逆も同様です。
最初に各文字を格納するために1バイトが使用されたと仮定すると、データをどれだけ削減できたかを計算できます。
入力に1000文字の文字列があり、文字a 1が500回、 2 240、3 150、および4 110回発生したとします。
最初、この文字列は8000ビットを占めていました。 コーディング後、長さ∑p i l i = 500 * 1 + 240 * 2 + 150 * 3 + 110 * 3 = 1760ビットの文字列を取得します。 そのため、ストリームの各シンボルのエンコードに平均1.76ビットを費やして、データを4.54回圧縮することができました。
シャノンによると、コードの平均長は
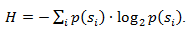。 この方程式に確率値を代入すると、1.75496602732291に等しいコードの平均長が得られます。これは、得られた結果に非常に近いものです。
ただし、データ自体に加えて、エンコードされたデータの最終サイズをわずかに増やすエンコードテーブルを格納する必要があることに注意してください。 明らかに、さまざまなケースでアルゴリズムのさまざまなバリエーションを使用できます-たとえば、事前定義された確率テーブルを使用する方が効率的である場合や、圧縮可能なデータを介して動的にコンパイルする必要がある場合があります。
おわりに
そのため、この記事では、ロスレス圧縮が発生する一般的な原理について話をしようとし、標準アルゴリズムの1つであるハフマンコーディングについても調べました。
記事がhabro-communityの趣味であれば、ロスレス圧縮に関してさらに多くの興味深いことがあるので、続編を書いてうれしいです。 これらは、古典的なアルゴリズムと予備的なデータ変換（たとえば、バロウズウィーラー変換）の両方であり、もちろん、音声、ビデオ、画像を圧縮するための特定のアルゴリズム（私の意見では最も興味深いトピック）です。
文学
- Vatolin D.、Ratushnyak A.、Smirnov M. Yukin V.データ圧縮方法。 デバイスアーカイバ、画像およびビデオ圧縮。 ISBN 5-86404-170-X; 2003年
- D.サロモン。 データ、画像、音声の圧縮。 ISBN 5-94836-027-X; 2004
- www.wikipedia.org