このトピックに興味を持って、私はこのアルゴリズムを実践しようとしましたが、途中で多くの熊手が私を待っていました。 まず第一に、何を正確に比較する必要がありますか? 時間領域の直接音声信号は長く、あまり効果的ではありません。 スペクトログラムはすでに高速ですが、それほど効率的ではありません。 最も合理的な表現の検索は、 MFCCまたはメル周波数ケプストラム係数につながりました。これらは、音声信号の特性としてよく使用されます。 ここでそれらが何であるかを説明しようとします。
基本的な概念
説明は、タイトルの最初の単語から始まります。 チョークとは? ウィキペディアは、チョークは聴覚器官によるこの音の知覚に基づくピッチの単位であると語っています。 ご存知のように、人間の耳の周波数応答は直接的なものとは似ておらず、振幅は音量の正確な測定値ではありません。 したがって、経験的に選択されたボリュームの単位、たとえばbackgroundを導入しました。
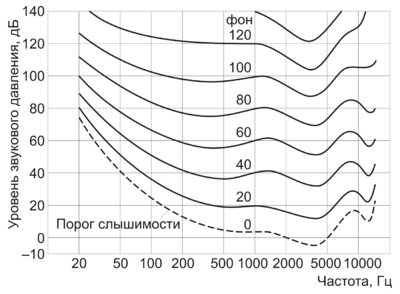
同様に、人間の聴覚で知覚される音のピッチは、その周波数にまったく直線的に依存しません。
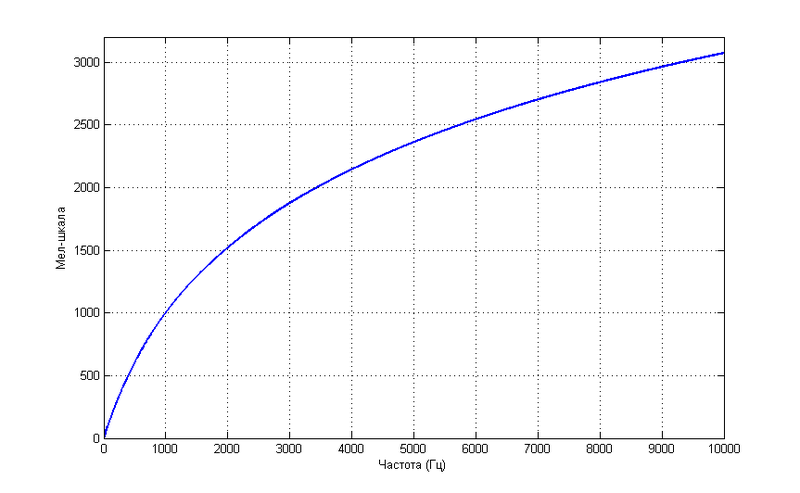
このような依存関係は、より正確であるふりをするものではありませんが、単純な式で記述されます

このような測定単位は、認識問題の解決によく使用されます。これは、既知の音声認識システムの中でこれまでのところリードしている人間の知覚のメカニズムに近づくことができるためです。
名前の2番目の単語- ケプストラムについて少し説明する必要があります。
音声形成の理論によれば、音声は器官系である肺、気管支、気管から放出され、声道に変換される音波です。 励起源と声道の形態が比較的独立していると仮定すると、人の音声装置は、トーンジェネレータとノイズジェネレータ、およびフィルタの組み合わせとして表すことができます。 概略的には、これは次のように表すことができます。

1.パルスシーケンスジェネレーター(トーン)
2.乱数ジェネレーター(ノイズ)
3.デジタルフィルター係数(音声パスパラメーター)
4.非定常デジタルフィルター
フィルターの出力(4)の信号は、畳み込みとして表すことができます。

ここで、s(t)は音響波の初期形態、h(t)はフィルター特性(声道のパラメーターに依存)です。
周波数領域では、このように見えます

代わりに製品をプロローグして合計を取得することができます

次に、この合計を変換して、元の信号とフィルターの特性の互いに素なセットを取得する必要があります。 これにはいくつかのオプションがあります。たとえば、逆フーリエ変換はこれを提供します

また、目標に応じて、直接フーリエ変換または離散コサイン変換を使用できます
基本的な概念を少し明確にしたいと思います。 音声信号をMFCC係数のセットに変換する方法を理解する必要があります。
例
テストとして、単純な数値1を取得します。これは、その一時的な表現です。
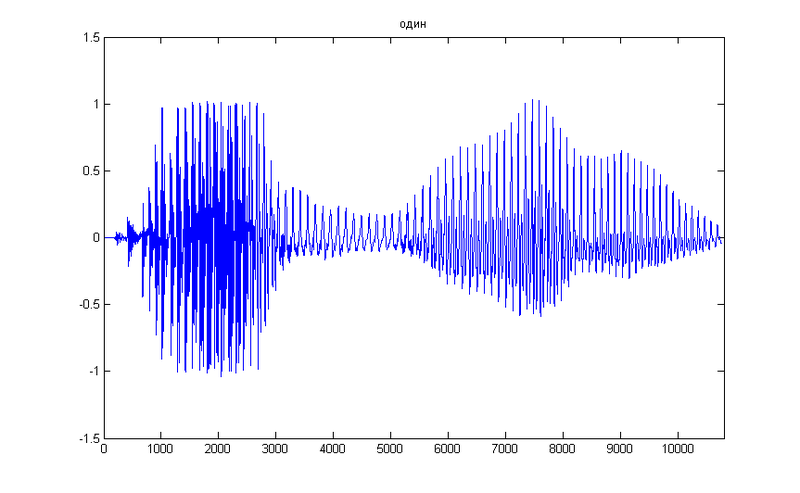
まず、フーリエ変換を使用して取得した元の信号のスペクトルが必要です。 例の単純化のために、信号を部分に分割しないため、時間軸全体に沿ってスペクトルを取得します

ここからが楽しみです。結果のスペクトルをチョークスケールで配置する必要があります。 これを行うには、チョーク軸上に等間隔のウィンドウを使用します。

このグラフを周波数スケールに変換すると、そのような写真を見ることができます

このグラフでは、ウィンドウが低周波領域で「収集」され、認識に必要な場所でより高い「解像度」を提供していることがわかります。
信号スペクトルのベクトルとウィンドウ関数を単純に乗算することにより、各分析ウィンドウに入る信号エネルギーを見つけます。 いくつかの係数のセットを入手しましたが、これらは私たちが探しているMFCCではありません。 これまでのところ、それらはメル周波数スペクトル係数と呼ばれていました。 平方と対数。 残っているのは、それらからケプストラムまたは「スペクトルスペクトル」を取得することだけです。 このために、もう一度フーリエ変換を適用できますが、 離散コサイン変換を使用することをお勧めします 。
その結果、およそ次のタイプのシーケンスが得られます。

おわりに
したがって、認識されると、音声信号の数千のサンプルを正常に置き換える非常に小さな値のセットがあります。 本は、単語認識問題について、計算された24個の係数のうち最初の13個を取得することが可能であると書いていますが、私の場合、16から始まる適切な結果が得られます。
より良い結果を得るには、ソースワードを短い期間のセグメントに分割し、それぞれの係数を計算します。 重み付けウィンドウ関数も役立ちます。 結果はすべて、認識アルゴリズムに依存します。
フォーミュラ
記事の主要部分に多数の式をロードしたくありませんが、突然誰かの興味を引くことになります。 したがって、私はそれらをここに持ってきます。
元の音声信号は離散形式で次のように書き込まれます。
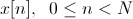
フーリエ変換を適用します
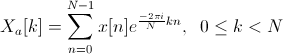
ウィンドウ関数を使用してフィルター櫛を作る

どの周波数f [m]について、等式から得ます

B(b)-頻度値のチョークスケールへの変換

各ウィンドウのエネルギーを計算する

DCTを適用する

MFCCキットを入手する
ソース
[1]ウィキペディア
[2] Xuedong Huang、Alex Acero、Hsiao-Wuen Hon、音声言語処理:理論、アルゴリズム、およびシステム開発ガイド、Prentice Hall、2001、ISBN:0130226165