
繰り返しますが、遠くから始めましょう。1つの製品の評価がどのように構成されるかを見てみましょう。 第一に、ユーザーが親切で、すべての人に良い評価を与えていることです。 または、逆に、怒りと評価のピンチ。 この基本的な要素を考慮しないと、何も機能しません。平均を調整しないと、さまざまなユーザーの評価を比較できません。 一方、一部の製品は他の製品よりも単純に優れている(または少なくともより優れたプロモーションが行われている)ため、同様の方法でこれも考慮する必要があります。
したがって、いわゆるベースライン予測子を導入することから始めます
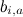 個々のユーザーの基本的な予測子で構成されます
個々のユーザーの基本的な予測子で構成されます 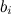 個々の製品の基本的な予測因子
個々の製品の基本的な予測因子 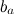 、およびベースμの全体的な平均評価だけでなく:
、およびベースμの全体的な平均評価だけでなく:
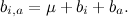
基本的な予測子のみを検索する場合、そのようなμを検索する必要があります。
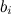 そして
そして 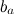 そのために
そのために 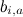 既存の評価に最も近い。
既存の評価に最も近い。
その後、実際の要因を追加することが可能になります-これで、基本的な予測子の調整を行ったので、残差はそれらの間で比較でき、合理的な要因を取得することができます。
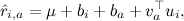
どこで
 製品aを表す因子のベクトルです。
製品aを表す因子のベクトルです。 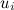 ユーザーiを表す因子のベクトルです。
ユーザーiを表す因子のベクトルです。
たとえば、基本的な予測変数を見つけるのは非常に簡単に思えます。データベース全体の平均評価を計算してみましょう。
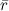 、それをμとして、各評価からそれを引き、平均評価を計算します
、それをμとして、各評価からそれを引き、平均評価を計算します 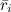 ユーザーによる
ユーザーによる  製品ごと。 ただし、これらの予測変数をこのように考慮することは誤りです。実際、これらの予測変数は互いに依存しており、一緒に最適化する必要があります。
製品ごと。 ただし、これらの予測変数をこのように考慮することは誤りです。実際、これらの予測変数は互いに依存しており、一緒に最適化する必要があります。
これで元の問題に戻って正確に述べることができます。近似する最適な予測子を見つける必要があります
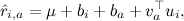
ここで「最高」とはどういう意味ですか? この質問に対する答えの最初の近似は次のとおりです。「最良の」とは、利用可能なデータで最も間違いを犯さないものです。 エラーを特定する方法は? たとえば、偏差の平方を追加することができます(ところで、平方はなぜですか?また、次のシリーズでこれについて説明します)。

しかし、そのような関数を最小化する方法は? はい、非常に簡単です-勾配降下法により、各引数に関して偏導関数を取得し、これらの偏導関数の方向と反対の方向に移動します。 エラー関数は2次曲面なので、ここで驚くことはありません。
ただし、ここで、取得した誤差関数Lから勾配降下の公式を書き出して実装すると、実際のデータセットでの実際の結果は満足できないでしょう。 一般的に言えば、予測子と因子の適切な値を訓練するために、機械学習の他の重要な概念である過適合と正則化を理解することは素晴らしいことであり、次のシリーズの1つで実際にこれを見るでしょう。 それまでの間、訓練された変数の値が大きすぎる場合は、まだ微調整する必要があると考えてください。 たとえば、すべての因子と予測変数の二乗和を誤差関数に単純に追加できます。
その結果、エラー関数は次のようになります
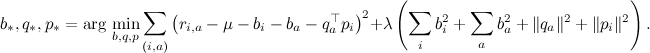
ここで、λは正則化パラメーターです。
最適化された変数ごとに偏微分を取得すると、(確率的)勾配降下の簡単な規則が得られます。

すべてのjについて 、ここで
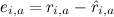 このテスト例のエラーで、γは学習率です。 このモデルはSVD ++と呼ばれ、Netflix賞の受賞モデルの基礎を築いたのは彼女でした(もちろん、彼女は一人で勝つことはできませんでした-なぜそれについても後で話しますか、何をすべきか)。
このテスト例のエラーで、γは学習率です。 このモデルはSVD ++と呼ばれ、Netflix賞の受賞モデルの基礎を築いたのは彼女でした(もちろん、彼女は一人で勝つことはできませんでした-なぜそれについても後で話しますか、何をすべきか)。
次回は、特定の例を分析しようとします。SVDを選好マトリックスに適用し、何が起こるかを分析し、主な困難を強調します。 おもしろいですね!