インターネットにはカルマンフィルターに関する記事や書籍が多数ありますが(主に英語)、これらの記事にはかなり高いしきい値があり、多くのあいまいな場所がありますが、実際には非常に明確で透明なアルゴリズムです。 私は彼について簡単な言葉で話そうとしますが、徐々に複雑さが増します。
それは何のためですか?
どの測定装置にも多少の誤差があり、それは多数の外部および内部の影響の影響を受ける可能性があり、その情報はノイズが多いという事実につながります。 データのノイズが多いほど、そのような情報を処理するのが難しくなります。
フィルターは、ノイズと過剰な情報を除去するデータ処理アルゴリズムです。 カルマンフィルターでは、システムの性質、変数の関係に関する先験的な情報を設定し、これに基づいてより正確な推定値を構築することが可能ですが、最も単純な場合(先験的な情報を入力せずに)でも優れた結果が得られます。
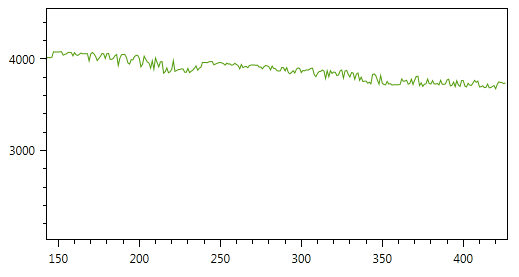
最も単純な例を考えてみましょう-タンク内の燃料レベルを制御する必要があるとします。 このため、容量性センサーがタンクに設置されており、メンテナンスが非常に簡単ですが、燃料補給への依存(燃料の誘電率は温度などの多くの要因に依存します)、タンク内の「チャター」の大きな影響など、いくつかの欠点があります。 その結果、そこからの情報は、適切な振幅を持つ典型的な「のこぎり」を表します。 このようなセンサーは、多くの場合、重い採掘設備に設置されます(タンクの容量と混同しないでください)
カルマンフィルター
少し脱線して、アルゴリズム自体に精通しましょう。 カルマンフィルターは、システムの動的モデル(運動の物理法則など)、既知の制御アクション、および最適な状態推定を形成するための多くの連続測定を使用します。 このアルゴリズムは、予測と調整の2つの繰り返しフェーズで構成されています。 最初に、次の瞬間の状態の予測が計算されます(測定の不正確さを考慮して)。 第二に、センサーからの新しい情報が予測値を修正します(この情報の不正確さとノイズも考慮に入れます):

線形代数がわからない場合は、方程式は行列形式で表示されます。大丈夫です。変数が1つの場合、行列のない単純化されたバージョンがあります。 単一変数の場合、行列はスカラー値に縮退します。
まず表記法を見てみましょう。下付き文字は時点を示します。kは現在の値、(k-1)は前のもの、上側のインデックスのマイナス記号はこれが予測される中間値であることを示します。
変数の説明は、次の図に示されています。
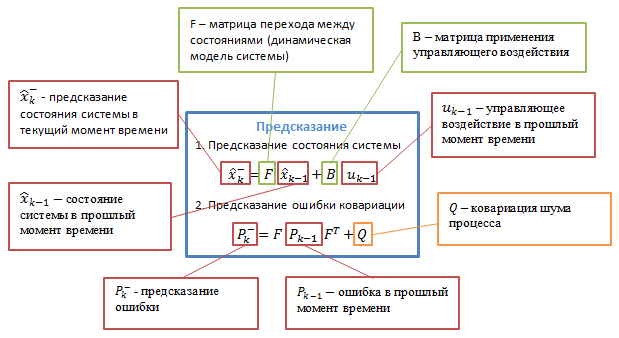
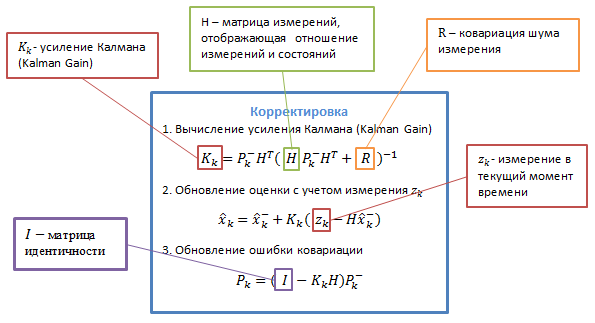
これらすべての不可解な遷移行列が意味することを長い間、退屈に説明することは可能ですが、私の意見では、実際の例を使用してアルゴリズムを試してみることをお勧めします。
でテストします
システムの状態は1つの変数(タンク内の燃料量)で表されるため、燃料レベルセンサーを使用した例に戻りましょう。マトリックスは通常の方程式に縮退します。
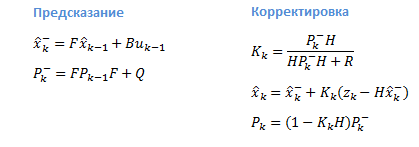
プロセスモデルの定義
フィルターを適用するには、システムのダイナミクスとF、B、Hの測定値を決定する変数の行列/値を決定する必要があります。
F-燃料の場合、システムのダイナミクスを記述する変数-サンプリング時間(アルゴリズムのステップ間の時間)のアイドル時の燃料消費を決定する係数にすることができます。 ただし、燃料消費量に加えてガソリンスタンドもあります。したがって、簡単にするために、この変数を1に設定します(つまり、予測値が前の状態に等しいことを示します)。
Bは、制御アクションの適用を決定する変数です。 エンジン速度またはアクセルペダルの踏み込み量に関する追加情報がある場合、このパラメーターはサンプリング中の燃料消費量の変化を決定します。 モデルには制御アクションがないため(それらに関する情報はありません)、B = 0を使用します。
Hは、測定値とシステムの状態との関係を定義する行列です。説明がない限り、この変数も1になります。
平滑化特性の決定
R-測定誤差は、測定器をテストし、測定の誤差を決定することにより決定できます。
Q-プロセスの分散を決定する必要があるため、プロセスノイズの決定はより難しいタスクです。これは常に可能とは限りません。 いずれの場合でも、このパラメーターを選択して、必要なレベルのろ過を提供できます。
コードで実装します
残りの不明瞭さを払拭するために、C#で単純化されたアルゴリズムを実装します(行列と制御アクションなし):
class KalmanFilterSimple1D { public double X0 {get; private set;} // predicted state public double P0 { get; private set; } // predicted covariance public double F { get; private set; } // factor of real value to previous real value public double Q { get; private set; } // measurement noise public double H { get; private set; } // factor of measured value to real value public double R { get; private set; } // environment noise public double State { get; private set; } public double Covariance { get; private set; } public KalmanFilterSimple1D(double q, double r, double f = 1, double h = 1) { Q = q; R = r; F = f; H = h; } public void SetState(double state, double covariance) { State = state; Covariance = covariance; } public void Correct(double data) { //time update - prediction X0 = F*State; P0 = F*Covariance*F + Q; //measurement update - correction var K = H*P0/(H*P0*H + R); State = X0 + K*(data - H*X0); Covariance = (1 - K*H)*P0; } } // ... var fuelData = GetData(); var filtered = new List<double>(); var kalman = new KalmanFilterSimple1D(f: 1, h: 1, q: 2, r: 15); // F, H, Q R kalman.SetState(fuelData[0], 0.1); // State Covariance foreach(var d in fuelData) { kalman.Correct(d); // filtered.Add(kalman.State); // }
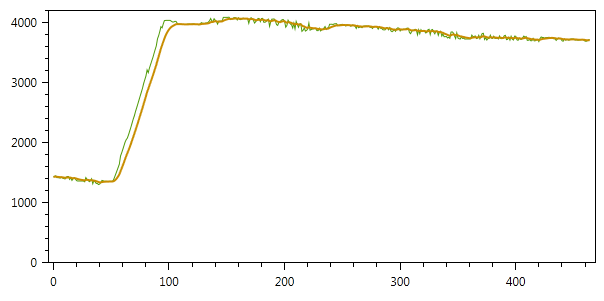
これらのパラメーターを使用したフィルター処理の結果を図に示します(平滑化の程度を調整するために、パラメーターQおよびRを変更できます)。
記事の外では、最も興味深いものが残っていました-いくつかの変数にカルマンフィルターを適用し、それらの関係と未観測変数の値の自動出力を設定します。 時間が来たらすぐにトピックを続けようとします。
質問や説明がある場合は、説明が非常に面倒で複雑ではないことを願っています-コメントへようこそ
UPD:ソースのリスト:
CS373-ロボットカーのプログラミング -強くお勧めします
ウィキペディア(ロシア語)
ウィキペディア
ハブ上: 1および2
より深刻なソース:
グレッグ・ウェルチ、ゲーリー・ビショップ、カルマン・フィルター入門、2001
MSGrewal、AP Andrews、「カルマンフィルタリング-MATLABを使用した理論と実践」、Wiley、2001
UPD2:この記事の例は、純粋にデモです。 フィルターの主な用途は、より複雑なシステムです。 たとえば、車の座標を決定する場合、GPS座標、ステアリング角度、エンジン速度などをリンクできます。これにより、座標の精度が向上します。