Clever Geek Handbook

相互作用するシーケンシャルプロセス（CSP）の理論の紹介



まえがき



このテキストは翻訳であり、 チャールズE.ホア による本の冒頭の章の要約された語りです。 目標は、ロシア語圏の聴衆を、プロセスの微積分のこの代数に慣れさせることです。この代数は、並列システムの広範な使用に関連して現代の計算科学で広く使用されています。 CSPの最も近く最も理解しやすい実用的なアプリケーションは、次のプログラミング言語になると思います。



CSPは、並列システムの相互作用を記述することができる正式な数学言語です。その主な用途は、 Transputerなどのシステムの並列動作の正式な仕様であり、さらに、信頼性の高い電子商取引サイトの開発に使用されます。

この記事では、この代数の基本について説明しますが、それなしではさらに学習することはできません。基本的に、これは本の最初の章の前半をカバーするプロセスの基本的な説明です。



はじめに



しばらくの間、コンピューターとプログラミングについて知っていることはすべて忘れてください。代わりに、特定の行動パターンに従って、私たちまたは相互に対話できる私たちの周りのオブジェクトについて考えてください。 お菓子の時計、電話、または自動販売機を想像してください。 最後のオブジェクトを例に取りましょう。それを説明するために、オートマトンの動作を決定し、それらに名前を付けます。 次に、コイン用のチョコレートバーを販売する単純な機械の場合、2つのアクションがあります。



小さなチョコレート（ルーブル用）と大きなチョコレート（ルーブル用）の2つのチョコレートを販売するより複雑な機械の場合、次のアクションを取得します。



このオブジェクトの説明に興味があるイベント名のセットは、 アルファベットと呼ばれます 。 アルファベットは、オブジェクトの不変の事前定義済みプロパティです。 チョコレート販売機が突然ラジコンタンクを提供することは不可能であるのと同様に、オブジェクトがアルファベットの外でアクションを実行することは論理的に不可能です。 しかし、同時に、チョコレートを販売するように設計されたマシンは、チョコレートが壊れたり、単にチョコレートが欲しくないという理由で単一のチョコレートを販売することはできませんが、このイベントにもかかわらず、 chocはマシンのアルファベットのままです。起こりません。



通常、アルファベットを選択するとき、状況を意図的に単純化し、オブジェクトのプロパティとアクションを意図的に無視します。これらはほとんど関心がありません。 たとえば、チョコレート販売機の重量、色、形状は説明されていません。チョコレートの供給を補充するなど、彼女の人生の確かに重要な瞬間も同様です。 このマシンを使用するとき、これらすべては特にエンドユーザーを心配しません。



各イベントはアトミックです。つまり、 すぐに起こります。 時間内に継続するイベントを記述するために、初期イベントと最終イベントのペアが使用されます。 それらの間隔で、他のイベントも発生する可能性があります。つまり、時間内に継続するイベントが重複する可能性があります。



別の詳細は、正確な実行時間から意図的に注意をそらすことです。これにより、説明が簡素化され、システムの計算速度に関係なく理論を適用できます。 実行時間が重要な場合、この問題は、システム設計の論理的な正確さとは別に検討する必要があります。



一時的な問題を無視すると、イベントの同時性を考慮しなくなります。 重要な場合（同期など）、これらのイベントを1つとして表示します。



アルファベットを選択するとき、外部から発生するイベント（ coin ）とオブジェクト自体が生成するイベント（ choc ）を分離する必要はありません。



オブジェクトの動作を説明するプロセスという用語を紹介します。これは、オブジェクトのアルファベットからの限られた数のイベントの観点から説明できます。 次の契約を順守します。

  1. 小さな文字で始まる単語は、個々のイベントを示します。たとえば、 coin 、 choc 、 in2p 、 out1p 、および個々の文字a 、 b 、 cなど。
  2. 大文字はプロセスを示します。例：

    • VMS-シンプルなトレーディングマシン
    • VMC-より複雑なトレーディングマシン
    さらに、文字P 、 Q 、 R （法律で使用）は、いくつかの任意のプロセスを示します

  3. 文字x 、 y 、 zはイベント指定変数です
  4. 文字A 、 B 、 Cは多くのイベントを示します。
  5. 文字X 、 Yはプロセス変数です
  6. プロセスアルファベットPは、たとえば次のようにαP（アルファP）として示されます。

    • αVMS= { コイン 、チョコ}
    • αVM= { in1p 、 in2p 、 small 、 large 、 out1p }
Aのイベントのいずれにも決して参加しないアルファベットAのプロセスは、 STOP Aとして指定されます。



プレフィックス


xをイベント、Pをプロセスとすると、次のようになります。

（ x → P ）（「x then P」と発音）


最初にイベントxを発生させ、次にPのように動作するオブジェクトを記述します。 定義により、プロセスPのアルファベットは（ x → P ）と同じですが 、もちろん、このエントリはxがこのアルファベットに属している場合にのみ使用でき、正式には次のように記述できます。

α（ x → P ）=αP条件x∈αPの下で


例：

  1. 1本のチョコレートバーが戻った後に壊れる簡単なトレーディングマシン：

    （コイン→ STOPαVMS ）
  2. 2人にサービスを提供した後に故障した簡単なトレーディングマシン：

    （コイン→（choc→（coin→（choc→ STOPαVMS ））））
    当初、機械はコインを受け入れることができますが、チョコレートバーを与えることはできませんが、コインが挿入された後、チョコレートバーが取り除かれるまで機械はコインを受け入れません。
  3. ポインターは、迷路に沿って、白いセルに沿って右上にのみ移動できます。

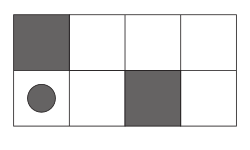
    αCTR= {上、右}

    CTR =（右→上→右→右→停止αCTR ）
3番目の例では、→が右側で結合しているという合意を受け入れることで括弧を省略して表記を簡略化しました。



次のエントリは構文に誤りがあることに注意してください。

P→Q

x→y
→左側のイベントを必ず受け入れる必要があります。 プレフィックスのチェーンはプロセスで終了する必要があります。 正しいエントリの例は、同等のエントリです。

x→（y→停止）

x→y→停止
したがって、イベントと1つ以上のイベントに参加しているプロセスを明確に区別します。



再帰


プレフィクスエントリを使用すると、最終プロセスの動作を説明できますが、自動販売機の場合、何百、何千もの販売で彼の生涯を説明するのは退屈です。 したがって、繰り返しのアクションを記述する方法が必要です。これにより、無限に続くプロセスを記述するための副次的な機会が得られます。



通常のカチカチ時計を検討し、そのカチカチだけに興味があることを考慮して、

αCLOCK= {tick}
クロックがチェックされた後、それらは同じクロックのままであり、ティックがクロックになった後のオブジェクトはクロックであると言えます。

CLOCK =（ティック→CLOCK）
右側のCLOCKを置き換えることにより、以下を受け取ります。 

 時計
     =（ティック→クロック）[初期方程式]
     =（ティック→（ティック→クロック））[1回のルックアップ]
     =（tick→（tick→（tick→CLOCK）））[2つの順列]
したがって、クロックの動作は、無限の数の繰り返しティックとして説明できます。

ダニ→ダニ→ダニ→・・・
この自己参照方法は、方程式の右側に接頭辞で始まる表現がある場合にのみ機能します。たとえば、方程式は次のようになります。

X = X
実際には何も決定しません すべてのプロセスがそれに対応します。 接頭辞「protected」で始まるプロセスの説明をさらに呼び出します。 したがって、F（X）がプロセス名XとαX= Aを含む保護された式である場合、方程式は次のようになります。

X = F（X）
アルファベットAを使用した独自のソリューションがあります。この方程式を次のように記述すると便利な場合がよくあります。

μX：A•F（X）
Xは変更可能なローカル変数です。

μX：A•F（X）=μY：A•F（Y）
これらの式の等価性は、方程式が

X = F（X）

Y = F（Y）
同じ解決策があります。



将来的には、プロセスを設定する両方の方法を使用します：方程式とμを使用します。 2番目のケースでは、アルファベットAの言及をしばしば省略します。 コンテキストから明らかです。



例：

  1. 無限の時計：

    クロック=μX：{tick}•（tick→X）
  2. 無数のチョコレートを販売する自動販売機：

    VMS =μX：（コイン→（choc→X））
    前述のように、このエントリは、より正式なエントリの短縮版です。

    VMS =μX：{コイン、choc}•（コイン→（choc→X））
  3. 5ルーブルコイン交換機：

    αCH5A= {in5p、out2p、out1p}

    CH5A =（in5p→out2p→out1p→out2p→CH5A）
  4. 同じアルファベットの交換機の別のバリアント：

    CH5A =（in5p→out1p→out1p→out1p→out2p→CH5A）


保護された式には解決策があり、置換メソッドを介して指で一意に表示することが可能であり、プロセスを式に置き換えて、それを拡張し、無期限に継続できるので、プロセスの任意の長い（しかし有限の）説明を書くことができ、 arbitrarily意的に長い時間のプロセスは同じように振る舞います、そして我々はそれらが同じであると言います。 本の以下の章に正確な数学的定義がなければ、より正式な証明は不可能です。



おわりに



この記事では、本の最初の章までは取り上げませんでしたが、CSPが何であり、どの言語を使用しているかについてのおおよその理解が得られることを願っています。 将来、最初の章では、選択肢（分岐を記述するため）、間接再帰（より複雑なプロセスを記述するため）が導入されます。 この原始的な装置に基づいて、プロセス代数の基本的な法則が証明されています。 最初の章の後半は、プロセスのトレース（実行されたプロセスのアクションの記録）および関連する操作に専念します。


More articles:


All Articles