🤣 🕺🏼 👩🏽‍🎓 幾何学的述語の正確な計算 👨🏻‍🏫 💅🏼 👬

皆さん、こんにちは。計算幾何学の基本的な側面、つまり述語の正確な計算に関する記事を読むことをお勧めします。

おそらくあなたの多くは、vychegeomaアルゴリズムの実装の「奇妙な」動作に遭遇しています：クラッシュと誤った結果。一般的に、これらの奇妙なことに驚くことはありません-これらは、浮動小数点演算の厳しい離散現実に連続ジオメトリを転送するコストです。アルゴリズムをデバッグして、魔法の定数を選択することでこのような問題を解決したことを提案します。ほとんどの場合、この方法で結果が得られた場合、おそらく一時的な結果になります。

この記事では、効率をほとんどまたはまったく損なうことなく、浮動小数点コンピューティングの欠点を取り除く方法を示します。記事の概要：

幾何学的述語「回転」;
ターンの「ナイーブな」実現の矛盾。
述語計算を簡素化するための区間演算の適用。
述語を計算するための長い算術およびいくつかの代替方法。
浮動小数点数で回転を計算する際の誤差の計算。

したがって、計算幾何学が「イプシロンの選択の科学」ではない理由と、幾何学的アルゴリズムを正しく効率的に実装する方法を知りたい場合は、クリックしてくださいこちら。

回す

一般に、離散構造としてのアルゴリズムは厳密に実装されます。述語の値がチェックされる条件付きブロックで問題が発生します（たとえば、ポイントが三角形の内側にあるかどうか、セグメントが四角形と交差するかどうかなど）。

たとえば、最も単純な幾何学的述語である回転を考えてみましょう。この入力述語は、平面上の3つの点を取ります

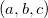cが有向セグメントabの左側にある場合は1を返します。 -1の場合、右側。 3つのポイントが同じライン上にある場合は0。述語は、ベクトル積を使用して実装されます。

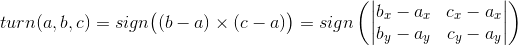
この述語は、その単純さにもかかわらず、非常に重要です。たとえば、セグメントのペアが交差するかどうか、ポイントが三角形の内側にあるかどうかなどをチェックするために使用できます。その実装を検討してください。

enum turn_t {left = 1, right = -1, collinear = 0}; double cross(point_2 const & a, point_2 const & b) { return ax * by - bx * ay; } turn_t turn(point_2 const & a, point_2 const & b, point_2 const & c) { double det = cross(b - a, c - a); if (det > 0) return left; if (det < 0) return right; return collinear; }

次の入力を使用してturn関数を呼び出すことを検討してください。

 point_2 a(3.0, 5.0); point_2 b = -a; point_2 c = a * (1LL << 52); turn_t res = turn(a, b, c); //  collinear

すべての点が1つの直線上にあるという事実にもかかわらず、結果は、浮動小数点演算の精度が限られているため、共線と等しくありません。多くの場合、ホットフィックスとして、ベクター製品が $v = (b - a)\times(c - a)$ 次の場合はゼロとみなすことができます $|v|$ 事前定義された定数e未満：

 double det = cross(b - a, c - a); if (det > e) return left; if (det < -e) return right; return collinear;

述部はすでに4つのポイントで互換性がないため、アイデアは失敗します。このような定数eの場合、述部が矛盾する結果を返すように4つのポイントを選択できます。たとえば、同じ直線セグメントabおよびcd上にない2つの平行線を考えます（図を参照）。

この図では、三角形 $v_1ab$ そして $v_2cd$ e / 2に等しい同じ面積を持ちます。三角形の2倍の面積は高さと底辺の積に等しいため、長いセグメントabのすべての点は、 cdに基づいて同じ面積の三角形を形成します。この領域は、 abとcdの頂点に基づいて同様に構成された三角形の領域よりも小さくなります。たとえば、特定の定数eの場合、セグメントabはセグメントcdと同一直線上にありますが、 cdはセグメントabと同一直線上にありません。

しかし、通常、共線性はかなりまれな結果です。ベクトル積を特定の定数と比較することにより、左と右のほとんどのターンを与え、効率の悪い、しかし正確な方法で（例えば、長い演算を使用して）答えの残りの部分を考慮することができれば、タスクが完了したと考えることができます。ターン計算時間は平均してわずかに長くなるためです。退屈な、しかし些細な計算を恐れない人のために、以下の付録で定数eの計算を行います。変更が行われた後、述部は次のようになります。

 double l = (bx - ax) * (cy - ay); double r = (cx - ax) * (by - ay); double e = (abs(l) + abs( r)) * std::numeric_limits<double>::epsilon() * 4; double det = l - r; if (det > e) return left; if (det < -e) return right; long_point_2 la(a), lb(b), lc( c); long_t ldet = cross(lb - la, lc - la); if (ldet > 0) return left; if (ldet < 0) return right; return collinear;

一般に、私たちはすでに完全に正しいかなり速い述語をすでに受け取っています。微妙な点が2つあります。第1に、もう少し加速できます。第2に、一般的な場合の定数eの公式の導出は、シンボリック算術（sympy、sageなど）の大きな助けにもかかわらず、かなり難しいタスクです。。）。インターバル演算を呼び出す時間です。

区間演算

区間演算の主な考え方は、浮動小数点境界を持つ特定のセグメントの実数を修正することです。浮動小数点演算で正確に表される数値は、縮退したセグメント（ポイント）で表されます。

2つの間隔を追加すると、それらの境界が追加されます。切り上げられた（プラスの無限大への）上限と、切り捨てられた（マイナスの無限大への）下限。次の考慮事項から残りの算術演算を決定するのは簡単です。実数の正確な値は不明であり、セグメント内の任意の値にすることができます。つまり、結果のセグメントには、オペランドセグメントの数値のすべてのペアに対する算術演算の結果が含まれている必要があります。

間隔演算には、ブースト/間隔など、いくつかの実装があります。

区間演算を使用すると、浮動小数点演算での述部計算の「信頼区間」をより正確に決定できます。明らかな理由で、区間演算は通常の演算よりも2〜5倍遅いですが、長い演算よりも約3〜4速いです。そのため、述語の実装では、従来の浮動小数点演算の後、長い演算を呼び出す前に信頼区間を明確にすることが理にかなっています。

 double l = (bx - ax) * (cy - ay); double r = (cx - ax) * (by - ay); double e = (abs(l) + abs( r)) * std::numeric_limits<double>::epsilon() * 4; double det = l - r; if (det > e) return left; if (det < -e) return right; interval_point_2 ia(a), ib(b), ic( c); interval<double> idet = cross(ib - ia, ic - ia); //     , , //    if (!zero_in(idet)) { if (idet > 0) return left; return right; } long_point_2 la(a), lb(b), lc( c); long_t ldet = cross(lb - la, lc - la); if (ldet > 0) return left; if (ldet < 0) return right; return collinear;

間隔の前に通常の算術演算を削除すると、計算速度は2〜5倍低下しますが、長い算術演算だけを残した場合のように3〜4桁は低下しません。場合によっては、この場合よりも述語の信頼区間を推定するのがはるかに困難であり、長い算術のパフォーマンスでは、それを計算の主要な手段として使用できません。この場合、区間演算は妥当な妥協案です。

ロング算術について

一般に、算術式の符号を正確に決定する方法は、長い演算だけではありません。 1.5のオーダーの長い演算よりも効率的なアルゴリズムがいくつかあります。これらはESSAおよび適応精度演算アルゴリズムです。インターネットでは詳細な説明を簡単に見つけることができるため、これらのアルゴリズムはここでは説明しません。デバッグ中に時間を節約できるコメントのみを行います：多くの場合、コプロセッサフラグは、計算が10バイト実数で実行されるように設定され、割り当てられたときに8または4バイト実数で丸められてプッシュされます。このため、計算の精度が向上しますが、これは前述のESSAおよびAdaptive Precision Arithmeticアルゴリズムに悪影響を及ぼします。それ以外の場合、これらのアルゴリズムは非常に移植性が高く、実装が非常に簡単です。

結論

この記事では、フィルター処理された述部の計算方法を紹介しました。フィルターの最初のステップ（浮動小数点演算）で、入力データのほとんどが効果的に選別されます。 2番目のステップ（間隔演算）では、最初のフィルターを通過した入力データの大部分が削除されます。 3番目のステップ（長い算術演算、ESSAまたは適応精度）では、前のステップを通過する残りのデータが処理されます。 1億個の入力データのテスト（正方形の均一分布）では、約20万個が区間演算に合格しました。長い算術演算に到達した入力はごくわずかであったため、このアプローチの有効性と単純性について楽観的な結論を導き出すことができます。このアプローチは一般的に受け入れられています。たとえば、計算幾何学のCGALライブラリで使用されます。タスクでは、入力データの性質に応じてフィルターを適切に使用できます。

参照資料

ご注意回転の定数eの計算

ここでは浮動小数点数について多くのことが書かれているので、いくつかの事実をリストします。

2進浮動小数点数は次のように表されます。 $a = \pm 1.a_1a_2a_3\dots a_{p - 1} \times 2^\gamma, a_i \in \{0, 1\}$ 。（実数に対する通常の操作とは対照的に）浮動小数点数にエラーがある操作は、通常次のように示されます。 $\oplus, \ominus, \otimes$ 。さまざまな著者がさまざまな方法で「マシンイプシロン」を定義していますが、この定義を使用します。 $\varepsilon = 2^{-p}$ 。たとえば、stlでは、イプシロンは2倍の大きさであることに注意してください。次に、最も近い値への丸めの対象となる操作のエラーは、次のように表現できます。

$a \oplus b = (a + b)(1 + \delta),\ |\delta| \leq \varepsilon$

$a \ominus b = (a - b)(1 + \delta),\ |\delta| \leq \varepsilon$

$a \otimes b = (a b)(1 + \delta),\ |\delta| \leq \varepsilon$

浮動小数点数で回転を計算します。

$\tilde{v} = (b_x \ominus a_x) \otimes (c_y \ominus a_y) \ominus (b_y \ominus a_y) \otimes (c_x \ominus a_x)$ 。

浮動小数点演算から実際の演算に移行しましょう。

$\begin{align*} \tilde{v} & = \bigl[(b_x - a_x)(c_y - a_y)(1 + \delta_1)(1 + \delta_2)(1 + \delta_3) \\ \quad{} & \quad{ } - (b_y - a_y)(c_x - a_x)(1 + \delta_4)(1 + \delta_5)(1 + \delta_6)\bigr](1 + \delta_7).\end{align*}$

次に、符号を正しく計算するための十分な条件を定式化します $\tilde{v}:\ |\tilde{v} - v| \leq e < |\tilde{v}|$ 。ある点を中心にボールを想像する $\tilde{v}$ および半径eを使用すると、この条件の正しさを確認できます。ボールにはゼロポイントが含まれないため、このボールのすべてのポイントは、ポイントvを含む同じ符号を持ちます。差係数を評価するために残っています $|\tilde{v} - {v}|$ 。デルタで括弧を開き、差分モジュールがモジュールの合計を超えず、製品モジュールがモジュールの製品と等しいことを思い出してください。

$|\tilde{v} - v| \leq \bigl(|(b_x - a_x)(c_y - a_y)| + |(b_y - a_y)(c_x - a_x)|\bigr) \times (4\varepsilon + 6\varepsilon^2 + 4\varepsilon^3 + \varepsilon^4).$

実数でeの下限を取得しましたが、 eは浮動小数点数です。に注意してください

$\begin{align*}\bigl(|(b_x - a_x)(c_y - a_y)| + |(b_y - a_y)(c_x - a_x)|\bigr) \times (1 -\varepsilon)^4 \leq\: \qquad{ } \\ \qquad{ } \leq \: |(b_x \ominus a_x)\otimes(c_y \ominus a_y)| \oplus |(b_y \ominus a_y)\otimes(c_x \ominus a_x)|.\end{align*}$

それはすぐに続きます：

$\begin{align*} |\tilde{v} - v| \leq \bigl(|(b_x \ominus a_x)\otimes(c_y \ominus a_y)| \oplus |(b_y \ominus a_y)\otimes(c_x \ominus a_x)|\bigr) \times\: \qquad{} \\ \qquad{} \times \: \frac{(4\varepsilon + 6\varepsilon^2 + 4\varepsilon^3 + \varepsilon^4)}{(1 -\varepsilon)^4}.\end{align*}$

上記から端数制限を取得するのは簡単です：

$\frac{(4\varepsilon + 6\varepsilon^2 + 4\varepsilon^3 + \varepsilon^4)}{(1 -\varepsilon)^4} \leq 8\varepsilon$

したがって、必要な定数eは次のように計算できます。

$e = \bigl(|(b_x \ominus a_x)\otimes(c_y \ominus a_y)| \oplus |(b_y \ominus a_y)\otimes(c_x \ominus a_x)|\bigr) \times 8\varepsilon.$

係数は2のべき乗であるため、実際の最後の乗算では、浮動小数点数のセットから数値が導出されないことに注意してください。

UPD。 タイプミスをしてくれたPortahとfsgsに感謝します。cross関数はpoint_2ではなくdoubleを返します。

UPD2。 Mrrlは、フィルターを再構築してパフォーマンスを向上させることが理にかなっている例を示しました。

幾何学的述語の正確な計算

回す

区間演算

ロング算術について

結論

参照資料

ご注意 回転の定数eの計算

More articles:

ご注意回転の定数eの計算