はじめに、または最初のAIを書いたとき
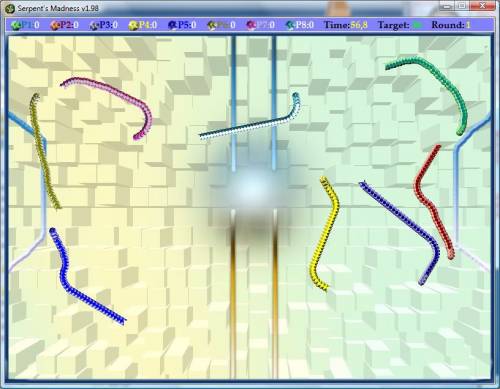
良い一日。 私が大学にいたとき、私は何年も前に私の最初の人工知能を書きました。 それはヘビの珍しいゲームであるヘビのAIでした- ヘビの狂気 (リンクは私のゲームWebサイトにつながります)で、後者は任意の方向に移動できます。 以下のスクリーンショットはこれを示しています。
そして、それは決定論的アルゴリズムでした。 アクションの明確なシーケンスを備えたアルゴリズム。各ステップで次に何が起こるかを正確に伝えることができます。 こんな感じでした (擬似コード):
rwarn = 0 //右側のヘビに対する危険
lwarn = 0 //左側のヘビに対する危険
すべての敵に対してop {
ポイントが敵の骨の中心である場合、opはヘビの半円内にあり、{
ポイントがヘビの右側にある場合、
rwarn ++;
ポイントがヘビの左側にある場合、
lwarn ++;
}
座標(xまたはy)の1つに沿った動きベクトルの最大偏差で、指定された距離以下で壁の1つに平行に移動する場合、{
壁がヘビの右側にある場合、
rwarn + = 100;
壁がヘビの左側にある場合、
lwarn + = 100;
}
rwarn!= 0およびlwarn!= 0の場合、{
rwarn> lwarnの場合、左に曲がります。 それ以外の場合は、右側に。
}
} //すべての対戦相手op
つまり このAIは、ヘビの特定の場所に対して常に同じことを行います。ヘビや壁が少ない側に向きを変えます。 はい、はい、マジックナンバー「100」を示しました。これは壁がある場合に危険を増加させます。 マジックナンバーは悪いプログラミングスタイルですが、当時は許されませんでした。 これは、ヘビが壁よりも他のヘビに頻繁に衝突するようにするためです。条件はかなり相対的です:ヘビの半円内に他のヘビの骨(=パーツ)が100を超える場合、アルゴリズムは壁に衝突することを選択します。 これにもかかわらず、アルゴリズムは非常にうまく機能しました.AIはさまざまな角度でヘビを一周し、壁を一周し(他のヘビがそれを強制しない限り、壁に衝突しませんでした)、実行する必要があるときに壁とヘビの間でバランスを取りました。
ただし、彼には2つの欠点がありました。
1)ヘビが壁の近くを移動していて、AIが壁とヘビの間にあったとき、どこかに行くべき場所があったとしても、次のことが定期的に発生しました:AIは混乱し、けいれんしました-左に少し、右に少し、左に少し...そして死にました。
2)ヘビから同じ所定の距離で、AIは常にターンを開始しました。 ヘビがAIから遠く離れていて、少し遅れて-はるかに短い距離(鋭くAIに向かっている)であることが判明した場合、AIはクラッシュしました。 彼が前に曲がることができるか、少なくとも曲がり始めることができれば。 大きな半径を持つ別の半円を導入することを考えていました。そのために「少し」回す必要があります。 それから私は自分にやめた アルゴリズムが複雑になってきたように思えます。 複雑にする場合は、確かにウェイポイントを入力してください-私は思った。
これらの2つの欠点は一言で表すことができます-場合によっては、ヘビは「痙攣」し、そのために時々死にました。
5年後、私はSerpent's Madnessをandroidに移植したとき、この欠点に対処することにしました。 そして、「ファジーロジック」がこれを助けてくれました。 ファジーロジックを、アルゴリズムに「ファジー」推論を導入するためのツールとして理解しています。 それでは、新しい視点からタスクを見てみましょう。
原理
Serpent's Madnessゲームのヘビは、左、右、または前方に移動できます。 彼女はまったく動けません。 したがって、AIには次の出力があります。
1)左に曲がる
2)右折
3)前進する
これに応じて、自然言語または人工言語のフレーズの意味をとることができる変数-言語変数を含む表を提示します。
| ヘビまでの距離 | ヘビ密度 | 壁までの距離 | 角を打つ | |
| 左側に | ||||
| 右へ | ||||
| 先に |
セルに用語があります。 用語では、変数のフレーズのまさに意味を意味します(言語学的)。
遠く、ちょうど近い-距離に関しては(列1および3)
いいえ、小、中、たくさん-ヘビの密度に関しては(列2)
いいえ、おそらく確かに-コーナーに入るとなると(列4)
各用語に対して、メンバーシップ関数が定義されています。 意味的には、これらは0から1までの「危険関数」であり、値が大きいほど、特定の方向に移動する危険が大きくなります。
行iごとに、セルm(i)の最大値を計算します。 それでは、与えられた方向のパラメーターに関して最大の危険性があるとしましょう。 次に、そのようなすべてのm(i)から最小値を見つけます。 少なくともこれが質問に対する答えになります-何をすべきか、左/右に曲がるか、まっすぐに進みます。
以下にいくつかの例を示します。 私は、数値解釈が例としてのみ与えられているという事実に注目します。 実際、開発されたシステムでは、他の値がある場合があります。
例1
| ヘビまでの距離 | ヘビ密度 | 壁までの距離 | 角を打つ | |
| 左側に | ちょうどいい | 少ない | いや | いや |
| 右へ | 遠く | いや | ちょうどいい | 確かに |
| 先に | 閉じる | たくさん | 遠く | いや |
結果は、左折する決定であるはずです。
計算から得られるもの:
min(max(0.5、0.33、0、0)、max(0、0、0.5、1)、max(1、1、0、0))= min(0.5、1、1)= 0.5 =左折
例2
| ヘビまでの距離 | ヘビ密度 | 壁までの距離 | 角を打つ | |
| 左側に | 閉じる | 中 | 遠く | いや |
| 右へ | 遠く | いや | 遠く | いや |
| 先に | 閉じる | 中 | 遠く | いや |
結果は右折の決定であるはずです。
min(max(1、0.75、0、0)、max(1、0.75、0、0)、max(0,0,0,0)= min(1,1,0)= 0 =右折
例3
| ヘビまでの距離 | ヘビ密度 | 壁までの距離 | 角を打つ | |
| 左側に | 閉じる | 中 | 遠く | いや |
| 右へ | 遠く | いや | 閉じる | いや |
| 先に | 閉じる | 中 | 遠く | いや |
その結果、決定を下すことは困難です-どこでも差し迫った死の危険があります。
ヘビが決めること:
min(max(1、0.75、0,0)、max(1、0.75、0、0)、(0,0、1、0))= min(1,1,1)= 1 =左折
私の観点では、次のことを論理に追加したいと思います。ヘビの同じ用語(近いとしましょう)は、壁よりも所属の度合いが低くなります。 これにより、差し迫った死で、壁ではなく、ヘビとのあらゆる方向の衝突を与えることができます-これはプレイヤーがより速くポイントを獲得できるようにするためです。
計算のルール
開発時には、次の点に注意します。 CPU時間を節約します。
1)max関数の項が計算され、1に等しい場合、残りを計算するポイントはありません。最大値は1になります。
2)min関数の項が計算され、0に等しい場合、残りを計算しても意味がありません。minは0を返します。
グラフィカルな解釈
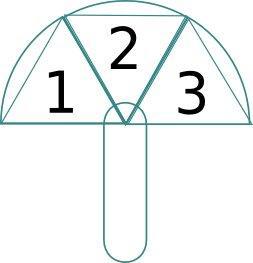
左、前、右-それぞれ1,2,3。 縦線はヘビのシンボルです。
これらは分析の領域です。 背後にあるものを分析することは意味をなさないので、エリア1と2は水平線で下に区切られます。 セクターを壁で「埋める」場合、使用されるのは(ヘビの骨の場合のように)円形セクターではなく、それに刻まれた三角形であることに注意してください。
用語のメンバーシップ関数の実装
次の3つの領域があることがわかります。
左、右、前。 これらのすべての領域は、円の半分、および個別にそれぞれ1/3のセクターになります。
セクターには以下が含まれます。
1)すべてのヘビの骨(ヘビ自体を含む-尾を回る必要があります)、すなわち、その座標と数
2)壁(最大2つ、角度に共通点がある場合)
このようなセクターは、「ヘビまでの距離」、「ヘビの密度」、「壁までの距離」、「コーナーを打つ」機能の入力に供給されます。 さらに帰属の度合いが戻ってきて、彼らと一緒に何をすべきかをすでに知っています。 関数自体も複雑ではありません。
最も難しい瞬間は、そのようなセクターを形成することです。
セクターの分野と責任
サークルセクタークラスCircleSector
動作:
1)ポイントがセクターに属していることを確認する
2)セクターが常に長方形の中央にあることに留意して、長方形との交点(0〜4ポイント)を見つけます。
3)ヘビの骨と壁に従って初期化する(上記の方法を使用)
4)分を見つける。 ヘビまでの距離(言語。変数1)
5)ヘビの密度を調べる(lingu。Trans。2)
6)分を見つける。 壁までの距離(ling。Trans。3)
7)角を打つ程度を調べる
8)最大の危険度を調べる
4から7-メンバーシップ関数の実装。
8-最大4-7を探します。
フィールド:
ポイント-ヘビの骨の座標(中心)
ポイント-壁セグメントの座標(0、2、3(角度)、4)
変更を加える
ファジーAIの最初のバージョンを実装した後、 Serpent's Madnessを起動すると、いくつかの欠点があります。
危険がないとき、蛇が回っていることが明らかになりました。
セクター内で同じ脅威値を持つminmax関数は、最初のセクターを返します。 そして、最初は正しいです。 最初の-フロントセクターを作りました。 これで、必要に応じて、デフォルトでヘビが前方に移動します。
私は、ヘビが壁に垂直に乗ると、壁に衝突することに気付きました。 この場合、分析は通常どおり続行されます(すべてが正しく初期化されます)。 垂直に移動する場合、すべてのセクターは1つの壁を等しく含み、前部セクターはそれぞれ「最も近い」と思われ、その中の脅威は最小限です。 これを修正し、前のセクターを他のセクターよりわずかに長くします。 その後、メンバーシップ関数は、壁に垂直に移動すると大きな脅威を返します。 他のセクターと比較して、セクターの半径がすでに1.1倍になっているため、このバグは軽減されます。
時々、ヘビは頭を一緒に、または4つもクラッシュさせます。 すべてのセクターが2倍に増加すると、衝突の頻度が少なくなることが実験的に確立されています。 しかし、その後、ヘビはあまりにも慎重になります-彼らが回す最小限の危険から遠く離れて、演奏はそれほど面白くなりません。 それでも、ヘビは「額」と衝突することがあります。 私の意見では、これはこの種の知性の問題です。次の時点で起こりうる敵の行動の分析をせずに、現時点では近くのエリアのみを分析します。
JavaおよびAndroid SDKリスト(v2.1)
そして今、私は動作中のコードを提供します。これは、何らかの理由で、ファジーロジックを使用した人工知能に関するほとんどの記事(私が見た)でめったに行われません。 長い蛇蛇の狂気でレベルをプレイすることで、このAIがどのように機能するかを明確に見ることができます。 記事の編集時、これは4番目のレベルです。
package com.iz.serpents.tools; import java.util.Collections; import java.util.LinkedList; import java.util.List; import android.graphics.RectF; import com.iz.serpents.model.Movement; import com.iz.serpents.model.Serpent; import com.iz.serpents.model.SerpentCollidable; /** * @author Deepscorn * There are three sectors, which in sum gives us one half of circle, * these sectors corresponds to aim, specified in constructor. * Each sector (LEFT, RIGHT, FORWARD) is 60 degrees. * So, sector is 1/6 of circle square. * */ public class CircleSector { /* * Checks if circle sector has the given point. * Algorithm is: * 1) check distance < radius * 2) check point is to the left of the first line * 3) check point is to the right of the second line */ public boolean hasPoint(Vector pt) { return (pt.qdist(O) < rad && pt.isOnLine(O, A)<0 && pt.isOnLine(O, B)>0); } /* * Creates sector * @param movementType - one of Movement.*, used in sector creation, different * movementTypes means different sectors * Note, that FORWARD sector will have radius greater, than specified in circleRadius. */ public CircleSector(float circleRadius, int movementType, Vector aim, Vector circleCenter) { if(movementType == Movement.FORWARD) rad = circleRadius * 1.1f; else rad = circleRadius; O = circleCenter; type = movementType; _ptBones = new LinkedList<Vector>(); _ptWalls = new LinkedList<Vector>(); Vector ortAim = (Vector) aim.clone(); ortAim.normalize(); Vector vC = ortAim.mul(rad); Vector vAC = null, vCB = null; if(type == Movement.LEFT || type == Movement.FORWARD) { vAC = (Vector) vC.clone(); vAC.qrotate(30, Movement.LEFT); } if(type == Movement.FORWARD || type == Movement.RIGHT) { vCB = (Vector) vC.clone(); vCB.qrotate(30, Movement.RIGHT); } switch(type) { case Movement.LEFT: Vector lo = (Vector) ortAim.clone(); lo.leftOrtogonalRotate(); A = O.add( lo.mul(rad) ); B = O.add(vAC); break; case Movement.FORWARD: A = O.add(vAC); B = O.add(vCB); break; case Movement.RIGHT: Vector ro = (Vector) ortAim.clone(); ro.rightOrtogonalRotate(); A = O.add(vCB); B = O.add( ro.mul(rad) ); break; } possibleBonesInside = (int) ((rad*rad)/ (6f*Serpent.boneRad()*Serpent.boneRad())); } /* * Fills sector with content */ public void addBones(List<? extends Serpent> serpents, int indAI) { _indAI = indAI; for(int j = 0;j<serpents.size();j++) { Serpent s = serpents.get(j); int start = 0; if(j==indAI) start = SerpentCollidable.afterNeckInd; for(int i=start;i<s.numBones();i++) { if(hasPoint(s.bone(i))) _ptBones.add(s.bone(i)); } } } /* * Gets number of bones in sector */ public int getNumBones() { return _ptBones.size(); } /* * Fills sector with content */ public void addWalls(RectF walls) { List<Vector> walls_points = new LinkedList<Vector>(); walls_points.add(Vector.create(walls.left, walls.top)); walls_points.add(Vector.create(walls.right, walls.top)); walls_points.add(Vector.create(walls.right, walls.bottom)); walls_points.add(Vector.create(walls.left, walls.bottom)); walls_points.add(Vector.create(walls.left, walls.top)); for(int i=0;i<walls_points.size()-1;i++) { Vector common; //left common = Vector.intersect(walls_points.get(i), walls_points.get(i+1), O, A); if(common!=null) _ptWalls.add(common); //right common = Vector.intersect(walls_points.get(i), walls_points.get(i+1), O, B); if(common!=null) _ptWalls.add(common); //forward common = Vector.intersect(walls_points.get(i), walls_points.get(i+1), A, B); if(common!=null) _ptWalls.add(common); //corner if(_ptWalls.size()==1) _ptWalls.add(walls_points.get(i+1)); } } /* * Gets number of wall's ends in sector: * 0 - no walls * 2 - one wall * 3 - two walls (corner) * 4 - two walls * wall is a line with two (!) ends */ public int getNumWallEnds() { return _ptWalls.size(); } /* * Gets distance to closest serpent in range [0;rad] * Attention! Distance = rad, when there actually * no serpents! */ public float distToClosestSerpent() { float res = rad; for(int i=0;i<_ptBones.size();i++) { float dist = _ptBones.get(i).qdist(O); if(dist < res) res = dist; } return res; } /* * Gets distance to closest wall in range [0;rad] * Attention! Distance = rad, when there actually * no walls! */ public float distToClosestWall() { float res = rad; for(int i=0;i<_ptWalls.size();i++) { float dist = _ptWalls.get(i).qdist(O); if(dist < res) res = dist; } return res; } //RELATION FUNCTIONS// //all relation functions returns value in ragne [0;1], //where 1 - is "the worst" or "the biggest" threat //and 0 - means no threat at all public float rel_distToClosestSerpent() { return 1 - distToClosestSerpent()/rad; } public float rel_serpentsStrength() { return ((float)getNumBones())/possibleBonesInside; } public float rel_distToClosestWall() { return 1 - distToClosestWall()/rad; } public float rel_inCorner() { float res = 0; if(getNumWallEnds()==4) res = 0.5f; if(getNumWallEnds()==3) res = 1f; return res; } public float rel_max_threat() { return Math.max( Math.max(rel_distToClosestSerpent(), rel_serpentsStrength()), Math.max(rel_distToClosestWall(), rel_inCorner())); } /* * Finds minimal threat and returns index of the element. * Keep in mind, that if all threats are equal, than the first * sector will be returned. */ public static int findMinThreatReturnIndex(ICircleSectorReadable sector[]) { float min = sector[0].rel_max_threat(); int result = 0; for(int i=1;i<sector.length;i++) { float cur = sector[i].rel_max_threat(); if(min>cur) { result = i; min = cur; } } return result; } //RELATION FUNCTIONS END// //sector geometry private Vector O; private Vector A; private Vector B; private final float rad; private final int type; private final int possibleBonesInside; //sector is presented as two lines: (O,A) - left line, (0,B) - right line, //O - is center of circle, which sector it is //rad - radius of circle, which sector it is //type is one of Movement.*, used in sector creation, different //movementTypes means different sectors //when working with walls there used triangular instead of circle center - for //performance reasons //initialed if necessary: //sector content private List<Vector> _ptBones = null; private List<Vector> _ptWalls = null; //sector owner private int _indAI; }
結果
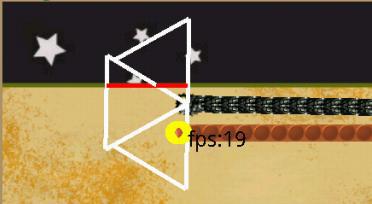
以下は、AIデバッグモードでのSerpent's Madnessのスクリーンショットです。
白はセクターの境界を示します-三角形(壁用、骨用-簡単に想像できます)。

セクターの骨は黄色で強調表示されます。

そして赤で-セクターの壁。
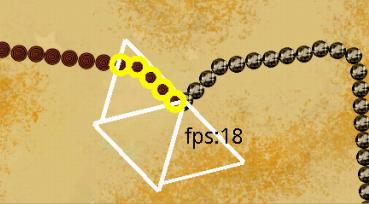
時には衝突します。 上で書いたように、これはセクターを増やすことで排除されます。 しかし、ゲームの一環として、無敵のAIは必要ありませんでした。
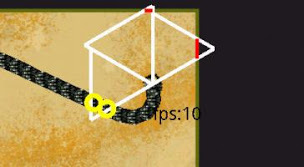
しかし、全体的に、AIは素晴らしいです。
これはAndroidプラットフォーム向けの最初の開発であり、ファジーロジックを備えた最初のAIです。提案やコメントがあれば、いつでも聞く準備ができています。 ご清聴ありがとうございました。 ゲームに興味がある場合は、Androidマーケットからダウンロードできます。
蛇の狂気