 しかし、逆の質問に興味がありました。たとえば、心臓のイメージをどのように持つか、グラフがこの心臓そのものになる関数の式をどのように取得するかです。
しかし、逆の質問に興味がありました。たとえば、心臓のイメージをどのように持つか、グラフがこの心臓そのものになる関数の式をどのように取得するかです。
フーリエ級数は覚えたくありませんでしたが、シンプルで美しいものが欲しかったのです。 この問題についてわかっている結果を思い出し始めました。 その結果、元の画像を幾分連想させる、画像に破線を生成するプログラムができました。 Woofという名前の子猫の例を使用すると、次のようになります(遠くからよく見えます)。
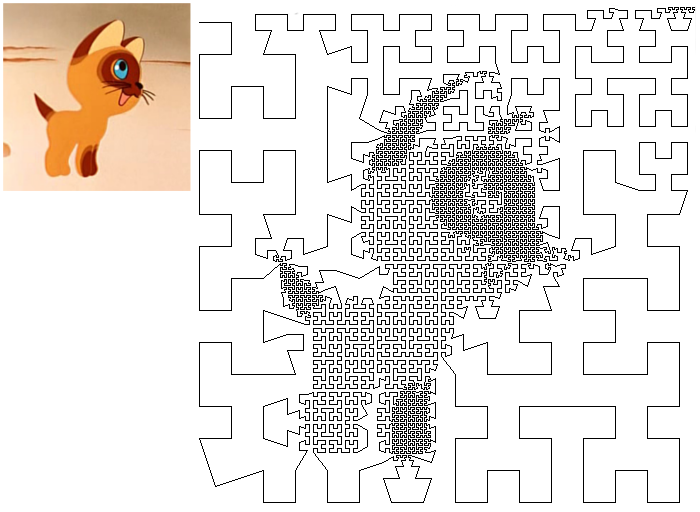
これを行う方法に興味があり、グラフが同じ数式である数式である麻の数式について学びたい場合は、habrakatへようこそ。 (多くの写真があります。)
それでは、いくつかの結果を思い出しましょう。
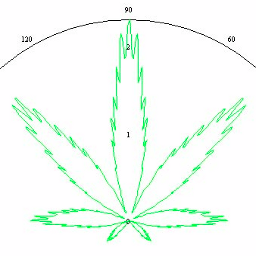
大麻式 。 2005年頃、ヘンプの処方が積極的に開発され、議論されました 。 フォームの極座標での単純な数式
- R ( t )=(1 + sin t )(1 + 0.9⋅cos 8 t )(1 + 0.1⋅cos 24 t )、
- R ( t )=(1 + sin t )(1-0.9⋅| sin 4t |)⋅(0.9 + 0.05⋅cos 200 t )、
- R ( t )=(1 + sin t )(1 + 0.9⋅cos 8 t )(1 + 0.1⋅cos 24 t )(0.5 + 0.05⋅cos 140 t )
アントン・スヒノフは何をしましたか? 彼は2005年にスイカフォーラムで次の複雑な式を提案しました(入力時に間違えなかった場合)。

次に、 F ( a 、 r )> 0のポイントのみを描画し、関数の値に応じて色を選択すると、次の画像が取得されます。

夢中になりませんか?
タッパー式 。 不平等を考慮する
 、数kを
、数kを
48584506361897134235820959624942020445814005879832445494830930850619347
04708809928450644769865524364849997247024915119110411605739177407856919
75432657185544205721044573588368182982375413963433822519945219165128434
83329051311931999535024137587652392648746133949068701305622958132194811
13685339535565290850023875092856892694555974281546386510730049106723058
93358605254409666435126534936364395712556569593681518433485760526694016
12512669514215505395545191537854575257565907405401579290017659679654800
64427829131488548259914721248506352686630476300
この不等式を満たし、0≤x≤106およびk≤y≤k + 17である点のセット( x 、y- k )は次のようになります。

そして、これは不平等そのものです。 もちろん、画像がkの間で単純に暗号化されていることは明らかですが、それでも結果は非常に美しく、そのようなものがどのように発明されたのかは明らかではありません。
詳細については、Wikipedia: Tupperの自己参照式を参照してください。特定の結果から大量メソッドに移行します。
反復可能な関数のシステム。 少なくともフラクタルの経験が少しでもある人なら誰でも、反復可能な関数のシステムが何かを知っているでしょう。 CIFでは、数十個の数字を使用して、実際の葉、木、枝に非常によく似た写真を取得できます。

与えられた画像からCIFを記述する一連の数値を取得するために、逆問題を解こうとする考えにより、マイケルバーンズリーはフラクタル圧縮を思いつくことができました。 フラクタル圧縮について話そうとするいくつかの試みは、すでにハブで行われています: フラクタル画像圧縮の基礎 。 しかし、詳細を理解したい人には、S。ウェルステッド著の「アクション中の画像を圧縮するためのフラクタルとウェーブレット」という本の前半をお勧めします。
フラクタルライン 。 実際、フラクタル圧縮アルゴリズムは、反復可能な関数のシステムではなく、いわゆる部分的な反復可能な関数のシステムを使用します。 それでも、CIFを思い付くのが簡単な画像のクラスがあります。 そのような画像はフラクタルラインです。 フラクタルラインは単語であり、各文字は特定の単語の縮小コピーなどで構成されます。 「HABR」という単語の例では、次のようになります。
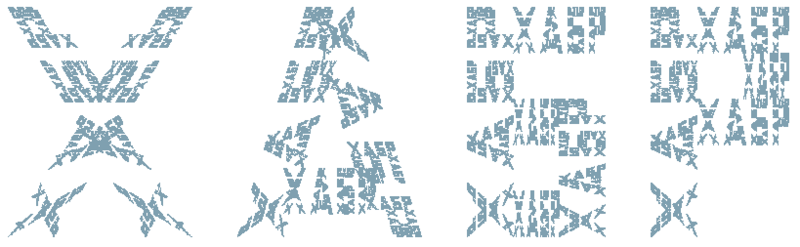
任意の単語に対してこれを行う方法を理解するのは簡単です。各単語を平行四辺形のセットとして表示するには少し時間をかけるだけで十分です。 少なくとも5年前にこれが行われました。 詳細な説明とコードは、記事Fractal Rowsにあります。
V.-J.の肖像 メラー。 フラクタル、カオス、べき法則の本をめくってください。 無限の楽園「M.シュレーダー」のミニチュア、次の図に出会えます。

それは非常に見栄えがよく、これが任意の画像で実行できることは明らかです。 この本は、それがどのように描かれたかを説明していませんが、自分で推測することは難しくありません。
まず、ヒルベルト曲線を作成するためのアルゴリズムを使用する必要があります。 しかし、Lシステムの助けを借りるのではなく、正直な再帰アルゴリズムを使用します。 そして、次のように変更します。 正方形の明るさが指定されたしきい値よりも大きく、4つのサブ正方形に曲線を描く必要がない場合、正方形自体に曲線を描く必要もないと仮定します。 おそらく、以下のコードから理解する方が簡単でしょう。
Point2D[] drawHilbertCurve(Point2D p, double size, int d) { Point2D q = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2), p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2)); if (size <= 2) { if (blockIsWhite(p, q)) { return null; } else { Point2D cc = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 2, p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 2); return new Point2D[]{cc, cc}; } } else { Point2D cl = new Point2D.Double( p.getX() + size * cos(PI * (d + 1) / 2) / 2, p.getY() + size * sin(PI * (d + 1) / 2) / 2); Point2D cc = new Point2D.Double( p.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 2, p.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 2); Point2D br = new Point2D.Double( p.getX() + size * cos(PI * d / 2), p.getY() + size * sin(PI * d / 2)); Point2D[] p1 = drawHilbertCurve(cl, size / 2, d - 1); Point2D[] p2 = drawHilbertCurve(cl, size / 2, d); Point2D[] p3 = drawHilbertCurve(cc, size / 2, d); Point2D[] p4 = drawHilbertCurve(br, size / 2, d + 1); if (p1 == null && p2 == null && p3 == null && p4 == null && blockIsWhite(p, q)) { return null; } else { if (p1 == null) { p1 = new Point2D[2]; p1[0] = p1[1] = new Point2D.Double( cl.getX() + size * sqrt(2) * cos(PI * (d - 0.5) / 2) / 4, cl.getY() + size * sqrt(2) * sin(PI * (d - 0.5) / 2) / 4); } if (p2 == null) { p2 = new Point2D[2]; p2[0] = p2[1] = new Point2D.Double( cl.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 4, cl.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 4); } if (p3 == null) { p3 = new Point2D[2]; p3[0] = p3[1] = new Point2D.Double( cc.getX() + size * sqrt(2) * cos(PI * (d + 0.5) / 2) / 4, cc.getY() + size * sqrt(2) * sin(PI * (d + 0.5) / 2) / 4); } if (p4 == null) { p4 = new Point2D[2]; p4[0] = p4[1] = new Point2D.Double( br.getX() + size * sqrt(2) * cos(PI * (d + 1.5) / 2) / 4, br.getY() + size * sqrt(2) * sin(PI * (d + 1.5) / 2) / 4); } drawLine(p1[0], p2[0]); drawLine(p2[1], p3[0]); drawLine(p3[1], p4[1]); } return new Point2D[]{p1[1], p4[0]}; } }
boolean blockIsWhite(Point2D p, Point2D q) { int l = (int) min(p.getX(), q.getX()); int r = (int) max(p.getX(), q.getX()); int t = (int) min(p.getY(), q.getY()); int b = (int) max(p.getY(), q.getY()); double c = 0; for (int i = l; i < r; ++i) { for (int j = t; j < b; ++j) { c += (srcImage.getRGB(i, j) & 0x0000FF) / 255.0; } } return c / ((b - t) * (r - l)) > threshold * (1 - log(2) / log(b - t)); }
画像がプログラムに送られる前に、グレーの色合いに変換され、実験的に明るさとコントラストが調整されました。 たとえば、プログラムがtuxに設定されたときに何が起こったのかを次に示します。

プログラムのソースコード 。
誰かが議論された領域から他の美しい結果を知っているなら、コメントでこれについて書いてください。