米国について簡単に:
- ルールと呼ばれる、ある部分文字列から別の部分文字列への置換のリストがあります
- リストの最初から、適用できる最初のルールを探し、最初のエントリに適用します
- そのようなルールが見つかった場合は、前の段落に戻って、最初にルールのリストを見てください
- ルールが最終的なものであれば、作業を完了します
- 適用できるルールがこれ以上ない場合は、作業を完了します。
それで、すべてが単純なように見えますか? しかし、米国でプログラムを書く方法は?
私自身のために、私はこの計画のようなものを作りました:
- 文字列のみを使用して通常のアルゴリズムを記述しようとしています
- 最後の置換が最初の置換と重複しないようにしてください
- アルゴリズムを裏返して、最後から最初に書き込みます
したがって、平方根の計算に戻ります。 数値の二乗は1から2n-1までの奇数の合計であるという単純な事実に基づいた「子供の」方法(算術でもあります)を使用します。
- 1 = 1 2 = 1
- 1 + 3 = 2 2 = 4
- 1 + 3 + 5 = 3 2 = 9
このプロパティに基づいてルート抽出を実装するにはどうすればよいですか? 数値がゼロより小さくなるまで、最初に1、次に3、次に5などのように、数値から順番に減算し、同時に減算の数をカウントします。 合計、すでに2つのカウンター+結果を保存するための1つの変数
米国の小さな特徴-ここに数字はありません。 そして、変数はありません。 したがって、それらをシミュレートする必要があります。 私は長い算術を書くのが面倒だったので(そして、それが人に可能だとは思わない)、単純な原則-インクリメントとデクリメントを使用して算術演算をしました。
私の文字列が{Result}の形式で保存されていることを確認することにしました。{Number} {Next Odd Number} {End of Line Indicator}
単項計算に奇数を格納し、ユニットを「#」として指定することにしました-作業がずっと簡単になります。
さて、データを失うことなく、数値から次の奇数をどのように引きますか? 奇数と行末インジケーターの間に、マーカー「a」を追加する必要があると判断しました。マーカー「a」は、番号を移動して、それを複製しますが、異なる形式(「-」で示されます)になります。 すべての短所を数字にシフトして、それらを削除します。 すべての数値を取り除いた後、結果を1つ増やす必要があります。
私の実装には小さな機能がありました-結果は常に切り上げられます。 このアルゴリズムを1でなく(説明のように)0.5の絶対精度で動作させることにしました。 行に初期値からマイナスが半分以上ある場合、結果を取得して削減する必要があります。
結果は、与えられた数の平方根を抽出する「ピンポン」です。
置換数の数への依存性は非常に興味深いように見えます。
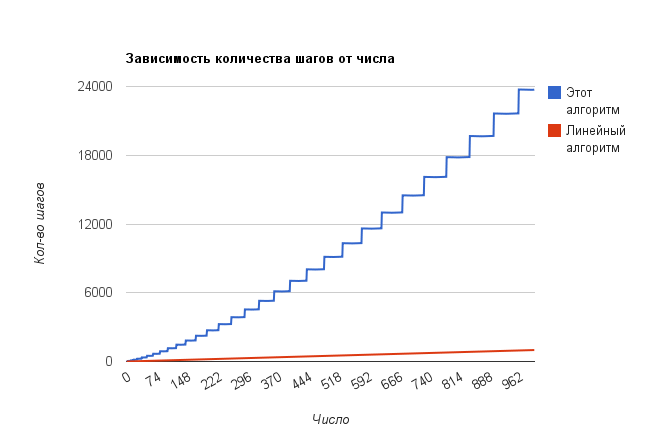
コードを表示: paste.org.ru/?3uweqh
実行例を表示: paste.org.ru/?34caeb
ダウンロードプログラム: sites.google.com/site/nsinreal/markovsqrt.zip