™️ 🙋🏾 🤜🏽 再び素数を見つけることについて ⬆️ 🧀 🧒🏻

このノートでは、素数を見つけるためのふるいアルゴリズムについて説明します。 エラトステネスの古典的なふるい 、一般的なプログラミング言語での実装の特徴、並列化および最適化を詳しく見てから、より現代的で高速なアトキンふるいについて説明します。エラトステネスのふるいに関する資料が主に初心者がレーキを定期的に歩くのを防ぐことを目的としている場合、アトキンのふるいアルゴリズムはHabrahabrで以前に説明されていませんでした。

写真は、スタンフォード大学のキャンパスに設置された抽象表現主義者のマーク・ディ・スヴェロの彫刻「エラトステネスのふるい」を示しています

はじめに

1つとそれ自体の正確に2つの異なる除数がある場合、その数は素数と呼ばれることを思い出してください。除数の数が多い数は複合と呼ばれます。 したがって、数値を因子に分解できる場合は、単純化のために数値をチェックすることもできます。たとえば、次のようなもの：

function isprime(n){ if(n==1) // 1 -    return false; //     2  sqrt(n) for(d=2; d*d<=n; d++){ //   ,   if(n%d==0) return false; } //    ,   return true; }

（以下、特に指定がない限り、JavaScriptのような擬似コードが提供されます）

このようなテストの実行時間は明らかにO （ ^n½ ）です。つまり、ビット長nに対して指数関数的に増加します。このテストは除数チェックと呼ばれます。

予想外に、除数を見つけることなく数の単純さをテストする方法がいくつかあります。多項式因数分解アルゴリズムが達成できない夢（RSA暗号化の強度に基づいている）である場合、2004年に開発されたAKS単純性テスト[ 1 ]は多項式時間で満たされます。さまざまな効果的な単純性テストが[2]にあります。

十分に広い間隔ですべての素数を見つける必要がある場合、最初の衝動はおそらく間隔からの各数を個別にテストすることです。幸いなことに、十分なメモリがある場合は、より高速な（そしてより単純な） ふるいアルゴリズムを使用できます。この記事では、そのうちの2つについて説明します。古代ギリシア人にも知られているエラトステネスの古典的なふるい 、およびこのファミリーの最も先進的な現代アルゴリズムであるアトキンふるいです。

エラトステネスのふるい

古代ギリシャの数学者エラトステネスは、与えられた数nを超えないすべての素数を見つけるために次のアルゴリズムを提案しました。長さnの配列Sを取り、単位で埋めます（ 非フレームとしてマークします ）。ここで、 k = 2から始まるS [ k ]の要素を順番に見ていきます。S[ k ] = 1の場合、 kの倍数であるすべての後続セルをゼロで埋めます（ クロスアウトまたはウィーブアウト ）。結果として、セル番号が素数である場合にのみ、セルに1が含まれる配列を取得します。

複合数がn未満の場合、除数の少なくとも1つが以下を超えないことに気付くと、多くの時間を節約できます。

、播種プロセスは終了するのに十分です

。ウィキペディアから取られたエラトステネスのふるいのアニメーションは次のとおりです。

同じ理由で、 2kからではなく数k ²から始めてkの倍数を消し始めれば、さらにいくつかの操作を保存できます。

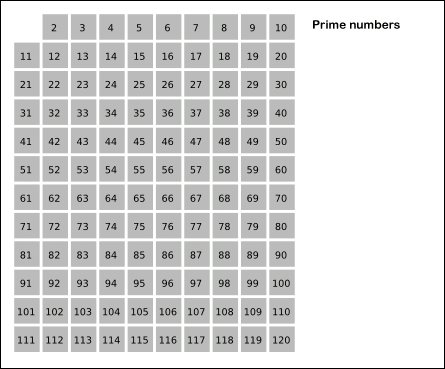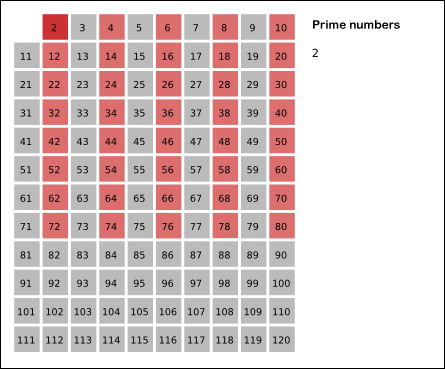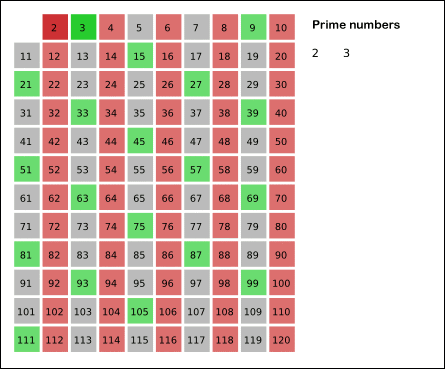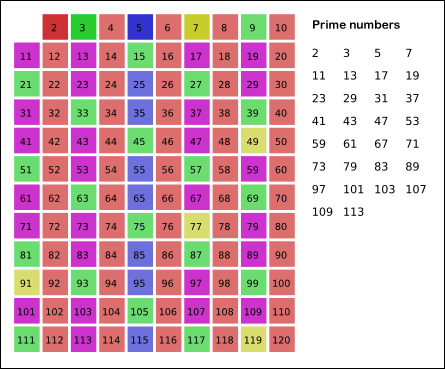
実装は次の形式を取ります。

 function sieve(n){ S = []; S[1] = 0; // 1 -    //    for(k=2; k<=n; k++) S[k]=1; for(k=2; k*k<=n; k++){ //  k -  ( ) if(S[k]==1){ //    k for(l=k*k; l<=n; l+=k){ S[l]=0; } } } return S; }

エラトステネスのふるいの有効性は、内部サイクルの極端な単純さによって引き起こされます。条件付き遷移、および除算や乗算などの「重い」操作は含まれていません。

アルゴリズムの複雑さを推定します。最初のストライクアウトにはn / 2アクション、2番目-n / 3、3番目-n / 5などが必要です。Mertensの式によると

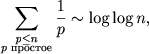
そのため、エラトステネスのふるいにはO （ n log log n ）操作が必要です。メモリ消費量はO （ n ）になります。

最適化と並列化

最初のふるいの最適化は、エラトステネス自身によって提案されました。すべての偶数のうち、2つだけが単純なので、メモリと時間の半分を節約しましょう。奇数のみを書き込み、播種します。アルゴリズムのこのような変更の実装には、表面的な変更（コード）のみが必要です。

より高度な最適化（いわゆるホイール因数分解 ）は、2、3、5を除くすべての単純なものが、次の8つの算術級数のいずれかにあるという事実に基づいています：30 k +1、30 k +7、30 k +11、 30 k +13、30 k +17、30 k +19、30 k +23および30 k +29。 nまでのすべての素数を見つけるには、事前に（ふるいを使用して）最大までのすべての素数を計算します

。 8つのシーブを構成します。各シーブには、 n未満の対応する算術級数の要素が含まれ、それぞれを別々のストリームにまきます。それだけです。メモリ消費とCPU負荷を削減するだけでなく（基本アルゴリズムと比較して4倍）、アルゴリズムの動作を並列化することもできます。

進行ステップとふるいの数を増やすことにより（たとえば、進行ステップが210の場合、48ふるいが必要になり、リソースをさらに4％節約できます）、 nの増加と並行して、log log n回アルゴリズムの速度を上げることができます。

セグメンテーション

すべてのトリックにもかかわらず、RAMが十分ではなく、アルゴリズムが恥知らずに「スワップ」する場合はどうすればよいでしょうか。 1つの大きなふるいを一連の小さなストレーナーに交換し、それぞれ個別に播種することができます。上記のように、簡単なリストを用意する必要があります

O （ ^n½-ε ）の追加メモリが必要です。ストレーナーの播種プロセスで見つかった単純なものを保存する必要はありません。すぐに出力ストリームに提供します。

同じO （ ^n½-ε ）エレメントよりも小さく、ストレーナーを小さくする必要はありません。したがって、メモリ消費の漸近的な動作では何も得られませんが、オーバーヘッドのために、パフォーマンスがますます失われ始めます。

エラトステネスふるいおよび単一ライン

Habrahabrは以前、さまざまなプログラミング言語の1行で、エラトステネスアルゴリズムの大規模な選択を公開しました（単一行10号）。興味深いことに、それらはすべてエラトステネスのふるいではなく、はるかに遅いアルゴリズムを実装しています。

事実は、条件でセットをフィルタリングすることです（たとえば、

 primes = primes.select { |x| x == prime || x % prime != 0 }

Rubyで）またはリスト内包表記ジェネレーターリスト（例：

 let pgen (p:xs) = p : pgen [x|x <- xs, x `mod` p > 0]

Haskellで）それらは、回避するためにふるいアルゴリズムと呼ばれるもの、つまり、分割可能性の要素ごとの検証を正確に呼び出します。結果として、アルゴリズムの複雑さは少なくとも次のように増加します。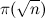

（これはフィルタリングの回数です）回

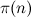（フィルタリングされたセットの最小要素数）、ここで

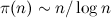-nを超えない単純な、つまりO （ n ^{3 /2-ε} ）アクションまでの数。

単線

 (n: Int) => (2 to n) |> (r => r.foldLeft(r.toSet)((ps, x) => if (ps(x)) ps -- (x * x to n by x) else ps))

Scalaでは、分割可能性チェックを回避するという点で、エラトステネスアルゴリズムに近いです。ただし、セットの差を構成する複雑さは、セットの大きい方のサイズに比例するため、結果は同じO （ n ^{3 /2-ε} ）操作になります。

一般に、エラトステネスのふるいは、不変変数の機能的パラダイムのフレームワーク内で効果的に実装することは困難です。関数型言語（OSamlなど）で許可されている場合、ルールに違反して可変配列を作成する価値があります。 [ 3 ]では、レイジーストライクアウトの手法を使用して、Haskellにエラトステネスのふるいを正しく実装する方法が議論されました。

エラトステネスとPHPのふるい

PHPでエラトステネスアルゴリズムを記述します。次のようなものが得られます。

 define("LIMIT",1000000); define("SQRT_LIMIT",floor(sqrt(LIMIT))); $S = array_fill(2,LIMIT-1,true); for($i=2;$i<=SQRT_LIMIT;$i++){ if($S[$i]===true){ for($j=$i*$i; $j<=LIMIT; $j+=$i){ $S[$j]=false; } } }

ここには2つの問題があります。これらの最初のものはデータ型システムに関連しており、多くの現代言語の特徴です。事実、エラトステネスのふるいは、メモリ内に連続して配置された同種の配列を宣言できる核施設で最も効果的に実装されています。次に、セルS [i]のアドレスの計算に必要なプロセッサー命令は2、3だけです。 PHPの配列は、実際には異種の辞書です。つまり、任意の文字列または数字によってインデックスが付けられ、さまざまなタイプのデータが含まれている場合があります。この場合、S [i]を見つけることは、はるかに時間のかかるタスクになります。

2番目の問題：PHPの配列はオーバーヘッドがひどいです。私の64ビットシステムでは、上記のコードの$ Sの各要素は128バイトを消費します。前述のように、ふるい全体をすぐにメモリに保存する必要はありません。部分的に処理できますが、そのようなコストは許容できないものとして認識される必要があります。

これらの問題を解決するには、より適切なデータ型-文字列を選択するだけで十分です！

 define("LIMIT",1000000); define("SQRT_LIMIT",floor(sqrt(LIMIT))); $S = str_repeat("\1", LIMIT+1); for($i=2;$i<=SQRT_LIMIT;$i++){ if($S[$i]==="\1"){ for($j=$i*$i; $j<=LIMIT; $j+=$i){ $S[$j]="\0"; } } }

現在、各要素はちょうど1バイトを使用し、ランタイムは約3倍減少しています。速度を測定するためのスクリプト。

アトキンふるい

1999年、アトキンとバーンスタインは、アトキンふるいと呼ばれる新しい合成数の播種方法を提案しました。次の定理に基づいています。

定理 nを、完全な正方形で割り切れない自然数とします。それから

nが 4 k +1として表現できる場合、式4 x ² + y ² = nの自然解の数が奇数である場合にのみ、それは簡単です。
nが6 k +1の形式で表現できる場合、式3 x ² + y ² = nの自然解の数が奇数である場合にのみ、それは単純です。
nが 12 k -1として表現できる場合、方程式3 x ² - y ² = nの自然解の数がx > yである場合にのみ、それは簡単です。

証明は[ 4 ]にあります。

素数理論から、すべての単純な大きな3は、12 k +1（ケース1）、12 k +5（再び1）、12 k +7（ケース2）、または12 k +11（ケース3）。

アルゴリズムを初期化するには、ふるいSをゼロで埋めます。次に、各ペア（ x 、 y ）について、

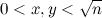、セルS [4 x ² + y ² ]、S [3 x ² + y ² ]、およびx > yの場合、S [3 x ² - y ² ]の値をインクリメントします。計算の終わりに、奇数を含む6 k ±1の形式のセルの数は素数であるか、または素数の平方に分割されます。

最後のステップとして、おそらく単純な数字を順番に調べ、それらの正方形の倍数を消します。

アトキンふるいの複雑さは、エラトステネスアルゴリズムのようにn log log nではなくnに比例することが説明からわかります。

著者の最適化されたCの実装はprimegenの形式で提示され、簡易版はWikipediaにあります。 Habrahabrでは、C＃のAtkinふるいが公開されました。

エラトステネスのふるいのように、ホイール因数分解とセグメンテーションを使用して、log logの漸近的複雑さをn倍、メモリ消費を最大O （ ^{n½+ o（1）} ）削減できます。

対数の対数について

実際、因子log log nは非常に大きくなっています。ゆっくり。たとえば、log log 10 10000≈10です。したがって、実用的な観点からは、一定であると想定でき、エラトステネスアルゴリズムの複雑さは線形です。単純な検索だけがプロジェクトの重要な機能ではない場合、エラトステネスのふるいの基本バージョンを使用して（偶数を保存）、これについて複雑にならないようにすることができます。ただし、単純なものを大きな間隔（2 ³²から）で検索する場合、ゲームはキャンドルの価値があり、アトキンの最適化とふるいは生産性を大幅に向上させることができます。

PSコメントはスンダラムのふるいを思い出させた。残念ながら、それは数学的な好奇心に過ぎず、エラトステネスとアトキンのふるい、または徹底的な除数によるチェックよりも常に劣っています。

文学

[1] Agrawal M.、Kayal N.、Saxena N. PRIMESはP. -数学の年報。 160（2）、2004。-P. 781–793。

[2] Vasilenko O. N.暗号の数論的アルゴリズム。 -M.、ICMMO、2003 .-- 328 p。

[3] O'Neill ME エラトステネスの本物のふるい。 -2008。

[4] Atkin AOL、Bernstein DJ Primeはバイナリ2次形式を使用してふるい分けします。 -数学。比較 73（246）、2003。-P. 1023-1030

再び素数を見つけることについて