
幸せを求めるのは無意味です。主なことは、あなたを見つける場所です。 私を含む一部の人は、この「幸福」のルートチケットをチェックする習慣になりました。最初の3桁の合計が他の3桁の合計と等しい場合、チケットは「幸福」と呼ばれます。 面白いですね、職業です。
しかし、時にはラッキーチケットが頻繁に出くわすことがあります。また、時には数か月間発生しないこともあります。 これは、任意のルートで1日1回旅行する場合です。
そして、ここには素晴らしい質問があります:「何枚の幸せなチケットが存在しますか?」そしてさらに良いことに、数学が同じように美しい質問を伴うとき:「幸せなチケットを購入する確率は?」
プログラミングの基礎を学んだ人にとって、この非常に多くの幸せなチケットを計算するプログラムを書くことは難しくありません-通常の列挙方法です。 結果を受け取って、55,251枚のチケットを受け取ったので、約18枚に1枚のチケットが幸せになります。
しかし今、指揮者のイメージを想像してみてください-数キログラムのささいなことと、彼が有料で順番に配るチケットのコイルを備えた首を通る男のバッグ。 そして、「010100」という番号のチケットの幸せな所有者になったらどうなりますか? そうです、指揮者がこのコイルを無くすまで、このルートには幸せなライダーはいません。
次に、この質問に数学的に答えてみましょう。
可能な最大のラッキーチケット「999999」のトライアド数は27 = 9 + 9 + 9 = 9 + 9 + 9です。 ラッキーディジットの合計が1に等しいチケットは9になります。これらはチケットです。
001001 010001 100001
001010 010010 100010
001100 010100 100100
ラッキーナンバーの合計が3に等しいチケットは36です。あなたは自分で計算できます-どんな方法でも。 そのような組み合わせごとにテーブルを作成しましょう。
トライアドの合計/グループ内のラッキーチケットの数
1/9
2/36
3/100
4/225
5/441
6/784
7/1296
8/2025
9/3025
10/3969
11/4761
12/5329
13/5625
14/5625
15/5329
16/4761
17/3969
18/3025
19/2025
20/1296
21/784
22/441
23/225
24/100
25/36
26/9
27/1
金額:55251
ラッキーチケットの最大数は、トライアドの合計が13または14のグループになります。

このようなコイルでは、1トライアドの2桁の合計が13 ... 14を超えるまで、9チケットごとにラッキーになります。 したがって、論理的には、このようなグループの18チケットごとに幸せになると想定できます。 そして、そのような「古典的な」分布を考慮して、000001から999999までのチケットのグループ全体で。
確率論の方法の1つを思い出して、計算します。
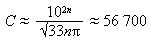
約3%の偏差で良好な精度で結果を取得します。
それでも、幸福のチケットは、この普遍的な幸福の急増を感じるために食べる必要があります。
幸せに!