もちろん、現代のすべてのプログラミング言語には、ランダム関数またはその類似物があります。 これらの関数は、ほとんどの場合、非常に優れた疑似乱数を生成しますが、これらの関数がどのように機能するのか、常に疑問に思っていました。
このトピックでは、線形合同法(ランダム関数で最もよく使用される)と、多項式カウンターを使用して乱数を取得する方法(機器をテストするためによく使用される)がどのように機能するかを説明します。
はじめに
均一な分布則でのみ乱数を生成するのが理にかなっているとすぐに言っておく価値があります。 他のすべての分布は、確率理論から既知の変換により、均一な分布から取得できます。
確率論を忘れているか、まだ理論を研究していない人のために、ゼロと1の均一に分布したシーケンスでは、ケースの50%で平均ゼロ(!)が発生することを思い出します。 しかし、これは、1000桁のシーケンスで正確に500個のゼロが存在することをまったく意味しません。 さらに、1000桁のシーケンスでは、999個のゼロが存在する可能性があり、1000番目の要素がゼロである確率は0.5のままです。 一見、これは逆説的なように見えますが、すべてのシーケンスが等しく発生する可能性があることを理解することが重要です。 そのようなシーケンスの十分に大きいセットを考慮すると、平均(!)でそれらのそれぞれに500個のゼロがあります。
理論を少し思い出して、歴史に移ります。 プレコンピューター時代には、バッグから多色のボールを引き出し、カードを引き、サイコロを投げることによって乱数が得られました。 この方法で本格的な研究を行うことは不可能であったことは明らかであるため、1927年にティペットは乱数の最初の表を公開しました。 少し後に、人々は何らかの形でこのプロセスを自動化しようとしました。 乱数を生成するマシンが現れ始めました。 現在、このようなデバイスも使用されており、エントロピーのソース(ジェネレーター)と呼ばれています。 このようなデバイスのみが真の乱数を生成できることに注意してください。 しかし、残念ながら、エントロピージェネレーターは非常に高価であり、すべてのPCにインストールすることはできません。 そのため、乱数を取得するアルゴリズムが必要です。
メモリ帯域幅を取得する最初の試み
乱数を取得するのは簡単だと思う人もいます。 彼らの意見では、このためには、元の数に対してランダムで複雑な数学演算を行うだけで十分です。 有名なKnutの2番目のボリュームを開くと、1959年にKnutもそのような考えに基づいてジェネレーターを構築しようとしたことがわかります。 彼のアルゴリズムは次のようになりました。
K1。 [反復回数を選択します。] Yに最大有効桁Xを割り当てます(ステップK2〜K13を正確にY + 1回実行します。つまり、ランダム化された変換をランダムな回数適用します)。
K2。 [ランダムなステップの選択]次に大きい有効桁Xを割り当てます。ステップK(3 + Z)、つまりプログラムでランダムに選択されたステップに進みます。
短絡。 [提供> 5 x 109] X <5,000,000,000の場合、XにX + 5,000,000,000の値を割り当てます。
K4。 [正方形の中央。] XをXの正方形の中央に置き換えます。
K5。 [乗算。] Xを数字(1001001001 X)mod 1010に置き換えます。
K6。 [疑似補数。] X <100000000の場合、Xに値X + 9814055677を割り当てます。 それ以外の場合は、Xを1010-Xに設定します。
K7。 [半分を再配置します。] 5つの低位文字を古い文字と交換します。
K8。 [乗算]ステップK5を実行します。
K9。 [数値を減らします。]数値Xの10進表現のゼロ以外の各桁を1つずつ減らします。
K10。 [99999に変更します。] A '<105の場合、X値を-X 2 +99999に割り当てます。 それ以外の場合は、XにX-99999の値を割り当てます。
K11。 [正規化](このステップでは、A 'をゼロに等しくすることはできません。)X <109の場合、Xに10を掛けます。
K12。 [二乗法の修正。] XをXの中央の10桁(X-1)に置き換えます。
K13。 [繰り返しますか?] Y> 0の場合、Yを1減らしてステップK2に戻ります。 Y = 0の場合、アルゴリズムは完了しています。 前の手順で取得した数値Xの値は、目的の「ランダムな」値になります。
明らかな複雑さにもかかわらず、このアルゴリズムはすぐに6065038420に収束しました。これは、わずかなステップを経て、それ自体に変換されました。 この話の教訓は、ランダムなアルゴリズムを使用して乱数を取得することはできないということです。
線形合同法
ほとんどのプログラミング言語では、このメソッドは乱数を取得するための標準関数で使用されます。 この方法は、1949年にレーマーによって最初に提案されました。 4つの番号が選択されています:
- モジュールm(m> 0);
- 係数a(0 <= a <m);
- 増分c(0 <= c <m);
- 初期値X 0 (0 <= X 0 <m)
シーケンスは、次の繰り返し式を使用して取得されます。Xn + 1 =(a * X n + c)mod m。
この方法は本当に良い擬似乱数を与えますが、m、a、cを任意に取ると、結果はおそらく失望するでしょう。 m = 7、X 0 = 1、a = 2、c = 4の場合、次のシーケンスが得られます:1,6,2,1,6,2,1、...
明らかに、このシーケンスはランダムの定義に完全には適合しません。 ただし、この失敗により、2つの重要な結論を導き出すことができました。
- 数字m、a、c、X 0はランダムであってはなりません。
- 線形合同法は、シーケンスを繰り返します。
実際、有限集合XをXにマッピングする関数は、周期的に繰り返される値を生成します。 T.O. 私たちのタスクは、シーケンスの一意の部分を可能な限り長くすることです(ところで、一意の部分の長さはmより大きくできないことは明らかです)。
証拠の詳細に立ち入らずに、次の3つの条件が満たされた場合にのみ、シーケンスの周期がmに等しくなると言います。
- 数字cとmは互いに素です。
- a-1は、mの約数である各素数pに対するpの倍数です。
- mが4の倍数である場合、a-1は4の倍数でなければなりません。
多項式カウンター(シフトレジスタ)に基づいて擬似乱数を取得する
ここで検討するアルゴリズムの基礎は、排他的OR演算(2を法とする合計)です。 念のため、この関数の真理値表がどのようなものかを思い出させてください:
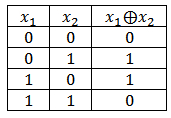
下図に示す回路は、最も単純な多項式カウンタです。 このようなスキームのゼロビットは排他的OR関数に基づいて計算され、他のすべてのビットは単純なシフトによって取得されます。 信号が排他的ORに送られるビットはタップと呼ばれます。
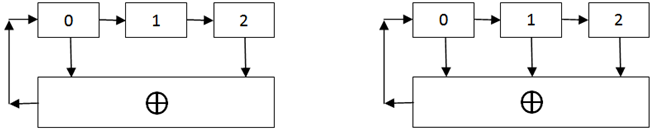
これらのレジスタの値が初期値001でどのように変化するかを検討してください。
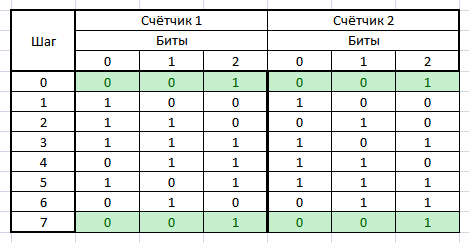
両方のレジスタは同じ値で機能し始めますが、レジスタによって生成された値はすぐに発散し始めます。 しかし、6つのステップの後、両方のレジスタは元の状態に戻ります。
これらのレジスタの両方が、ゼロ以外のすべての組み合わせを含む最長のシーケンスを生成したことを示すのは簡単です。 つまり レジスタのビット幅がmの場合、長さ2 m -1のシーケンスを取得できます。
任意の容量の多項式カウンターには、最大長のシーケンスを提供するタップの組み合わせがいくつかあります。誤った組み合わせを使用すると、短いシーケンスが生成されます。 個別のかなり難しいタスクは、これらの曲げの組み合わせを検索することです。
これらの組み合わせは必ずしも一意ではないことに注意してください。 たとえば、10ビットカウンタの場合、[6; 9]と[2; 9]の2つがあります。6桁のカウンタの場合、そのような組み合わせは28個あります。
これらの組み合わせを見つけるには、多項式の形式でカウンターを提示する必要があります。 この例のカウンターは、x 2 XOR 1およびx 2 XOR x XOR 1のようになります。
理論から、完全なシーケンスを生成するための必要十分条件は、特性多項式の原始性であることが知られています。 これは次のことを意味します。
- 特性多項式は、低次の多項式の積として表すことはできません。
- 特性多項式は、(δ= 2 m -1に対する多項式zδXOR 1の約数であり、δ<2 m -1の他の値の約数ではありません。
多項式カウンターの利点は、ソフトウェアとハードウェアの両方の実装が簡単である点、操作の速度、暗号強度です。
この記事がお役に立てば幸いです。