理論
近似関数f(x)の値がN + 1ノードf(x 0 )、...、f(x N ) で与えられるとします。 いくつかのパラメトリックファミリーF(x、c)から近似関数を選択します。ここで、 c =(c 0 、...、c n ) TはパラメーターのベクトルN> nです。
RMS近似問題と補間問題の根本的な違いは、ノードの数がパラメーターの数を超えることです。 この場合、ほぼすべてのノードで近似関数の値が近似関数の値と一致するようなパラメーターのベクトルはほとんどありません。
この場合、近似問題は、パラメーターc =(c 0 、...、c n ) Tのそのようなベクトルを見つける問題として提起されます。ノード。
グラフィカルに、問題は次のように表すことができます
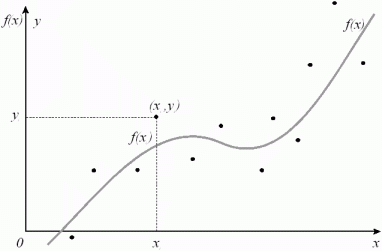
最小二乗法のrms近似基準を記述します。
J(c)=√(Σi = 0 N [f(x i )-F(x、c)] 2 )→min
ラジカル式は、近似多項式の係数に関する2次関数です。 c 0 、...、c nに関して連続で微分可能です。 明らかに、その最小値は、すべての偏導関数がゼロに等しい点にあります。 偏微分をゼロに等しくすると、最良近似の多項式の未知の(望ましい)係数の線形代数方程式系が得られます。
最小二乗法はさまざまなパラメトリック関数に適用できますが、工学の実践では、多項式が線形独立ベースで近似関数として使用されることがよくあります{ φk(x)、k = 0、...、n }:
F(x、c) =Σk = 0 n [ c kφk(x) ] 。
この場合、係数を決定するための線形代数方程式のシステムは非常に明確な形式になります。
a 00 c 0 + a 01 c 1 + ... + a 0n c n = b 0
a 10 c 0 + a 11 c 1 + ... + a 1n c n = b 1
...
a n0 c 0 + a n1 c 1 + ... + a nn c n = b n
a kj =Σi = 0 N [φk(x i )φj(x i )]、b j =Σi = 0 N [f(x i )φj(x i )]
このシステムに独自のソリューションを持たせるには、行列Aの行列式(グラム行列式)がゼロ以外であることが必要かつ十分です。 システムが独自の解をもつためには、基底関数系φk (x)、k = 0、...、nが近似ノードのセットに線形に独立していることが必要かつ十分です。
この記事では、パワー基底{ φk(x)= x k 、k = 0、...、n }の多項式による平均二乗近似について説明します。
例
それでは、例に移りましょう。 最小二乗法を使用して、表依存f(x)の経験式を導き出す必要があります。
| x | 0.75 | 1,50 | 2.25 | 3.00 | 3.75 |
| y | 2,50 | 1.20 | 1.12 | 2.25 | 4.28 |
近似関数として取ります
y = F(x)= c 0 + c 1 x + c 2 x 2 、つまり、n = 2、N = 4
係数を決定するための方程式系:
a 00 c 0 + a 01 c 1 + ... + a 0n c n = b 0
a 10 c 0 + a 11 c 1 + ... + a 1n c n = b 1
...
a n0 c 0 + a n1 c 1 + ... + a nn c n = b n
a kj =Σi = 0 N [φk(x i )φj(x i )]、b j =Σi = 0 N [f(x i )φj(x i )]
係数は次の式で計算されます。
a 00 = N + 1 = 5、a 01 =Σi = 0 N x i = 11.25、a 02 =Σi = 0 N x i 2 = 30.94
a 10 =Σi = 0 N x i = 11.25、a 11 =Σi = 0 N x i 2 = 30.94、a 12 =Σi = 0 N x i 3 = 94.92
a 20 =Σi = 0 N x i 2 = 30.94、a 21 =Σi = 0 N x i 3 = 94.92、a 22 =Σi = 0 N x i 4 = 303.76
b 0 =Σi = 0 N y i = 11.25、b 1 =Σi = 0 N x i y i = 29、b 2 =Σi = 0 N x i 2 y i = 90.21
連立方程式を解き、次の係数値を取得します。
c 0 = 4.822、c 1 = -3.882、c 2 = 0.999
このように
y = 4.8-3.9x + x 2
結果の関数のグラフ
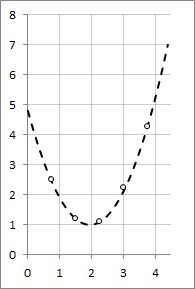
C#リリース
次に、そのようなマトリックスを作成するコードの作成方法に進みましょう。 そして、ここで判明したのは、すべてが非常に単純なことです。
private double[,] MakeSystem(double[,] xyTable, int basis) { double[,] matrix = new double[basis, basis + 1]; for (int i = 0; i < basis; i++) { for (int j = 0; j < basis; j++) { matrix[i, j] = 0; } } for (int i = 0; i < basis; i++) { for (int j = 0; j < basis; j++) { double sumA = 0, sumB = 0; for (int k = 0; k < xyTable.Length / 2; k++) { sumA += Math.Pow(xyTable[0, k], i) * Math.Pow(xyTable[0, k], j); sumB += xyTable[1, k] * Math.Pow(xyTable[0, k], i); } matrix[i, j] = sumA; matrix[i, basis] = sumB; } } return matrix; }
入力で、関数は関数値のテーブルを受け取ります。その行列の最初の列にはxの値、2番目にはyの値、およびべき乗基底の値が含まれます。
最初に、行列にメモリが割り当てられます。これには、連立一次方程式を解くための係数が書き込まれます。 次に、実際には、マトリックスを構成します-係数aijの値は、理論部分で上に示した式に従って、sumA、biB sumBに書き込まれます。
線形代数方程式のコンパイルされたシステムを解くために、私のプログラムはガウス法を使用しています。 プロジェクトのアーカイブはここからダウンロードできます 。
上記で解決した例を使用したプログラムのスクリーンショット:
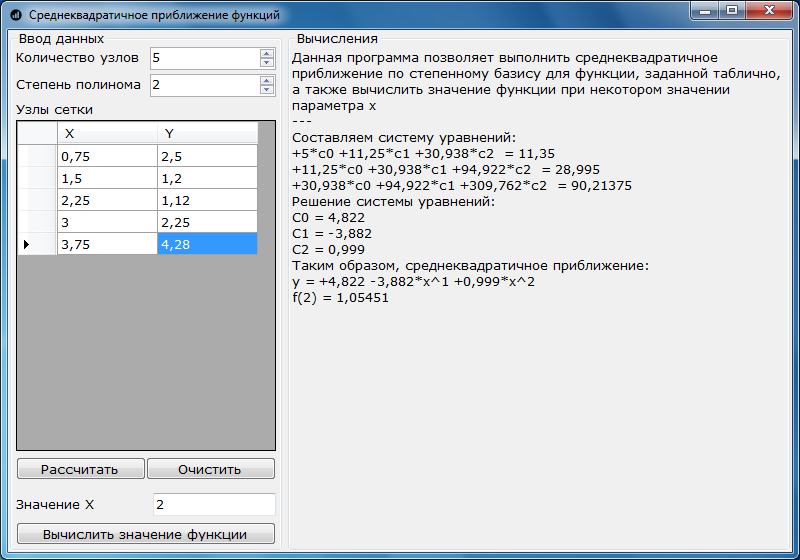
使用されたソース:
スリモバV.V. コース「計算ワークショップ」のガイドライン-Tula、TulSU、2009-65 p。