再循環ネットワークは、直接Y = f(X)と逆X = f(Y)の両方の情報変換によって特徴付けられます。 このような変換のタスクは、ベクトルXの最良の自動予測または自己再現性を実現することです。リサイクルニューラルネットワークを使用して、元の(逆変換)情報を圧縮(直接変換)および復元します。 そのようなネットワークは、その過程で自己組織化されます。 1988年に提案されました。 再循環ニューラルネットワークの理論的基礎は、主要コンポーネントの分析です。
主成分法
主成分分析の方法は、情報コンテンツを大幅に失うことなく情報を圧縮するために統計で使用されます。 これは、次元nの入力ベクトルXから次元pの出力ベクトルYへの線形直交変換で構成されます(p <n)。 さらに、ベクトルYの成分は無相関であり、変換後の総分散は変化しません。 入力パターンのセットは、マトリックスの形式で表示されます。
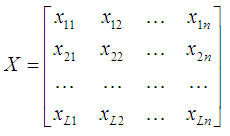
どこで
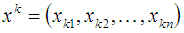
k番目の入力画像に対応し、Lは画像の総数です。
行列Xが中心にある、つまり数学的な期待ベクトルµ = 0であると仮定します。 これは、次の変換を使用して実現されます。
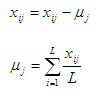
入力Xの共分散行列は次のように定義されます
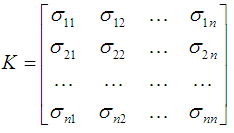
ここで、σijは、入力画像のi番目とj番目の成分間の共分散です。
共分散行列の要素は、次のように計算できます。
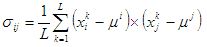
ここで、i、j = 1、...、n。
主成分の方法は、初期変数のそのような線形結合を見つけることから成ります
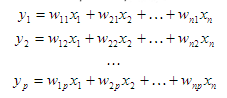
なに
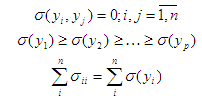
最後の式から、変数yiは相関関係がなく、分散が増加するように順序付けられ、入力画像の分散の合計は変化しません。 次に、最初のp変数yのサブセットが、分散全体の大部分を特徴付けます。 結果は、入力情報の表現です。
変数y、i = 1、...、pは、主要コンポーネントと呼ばれます。 マトリックス形式では、主要コンポーネントの変換は次のように表すことができます。
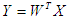
ここで、行列WTの行は直交性の条件を満たす必要があります。
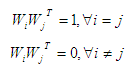
ベクトルWiは

主成分を決定するには、重み係数Wi、j = 1、...、pを決定する必要があります。
再循環ニューラルネットワークアーキテクチャ
再循環ニューラルネットワークは、双方向リンクで相互接続された2つの層のニューラル要素の組み合わせです。
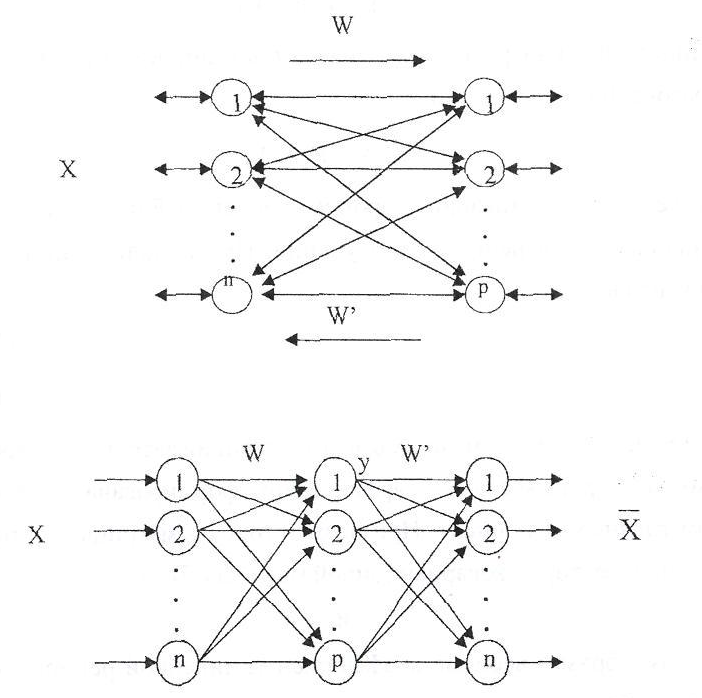
ニューラル要素の各レイヤーは、入力または出力として使用できます。 ニューラル要素の層が入力として機能する場合、分布機能を実行します。
それ以外の場合、レイヤーのニューラル要素が処理されています。 直接およびフィードバックに対応する重みは、重みの行列WおよびW 'によって特徴付けられます。 明確にするために、再循環ネットワークは拡張された形式で提示できます。
このようなネットワークの表現は同等であり、情報変換の完全なサイクルを特徴づけます。 この場合、ニューラル要素の中間層は入力データXをエンコード(圧縮)し、最後の層は圧縮情報Yを復元します。通信行列W directに対応するニューラルネットワークの層と、対応する通信行列W 'を逆に呼び出します。
再循環ネットワークは、データ圧縮と圧縮された情報の回復の両方のために設計されています。 データ圧縮は、次の式に従って情報を直接変換して実行されます。
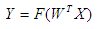
データの回復または再構築は、情報の逆変換中に発生します。

神経要素Fの活性化の関数として、線形関数と非線形関数の両方を使用できます。 線形アクティベーション機能を使用する場合:
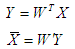
主成分法に従って重みが決定される線形再循環ネットワークは、SARネットワークと呼ばれます。
画像処理
再循環ニューラルネットワークを使用して、画像を圧縮および復元できます。 画像はブロックに分割されます。 ブロックは、再循環ニューラルネットワークが割り当てられるウィンドウと呼ばれます。 ネットワークの最初の層のニューロンの数は、ウィンドウの次元に対応します(ピクセルの数。各色が異なる場合があります)。 ウィンドウを使用して画像をスキャンし、ニューラルネットワークに送信することにより、入力画像を圧縮できます。 圧縮された画像は、情報の後方拡散を使用して復元できます。
ニューラルネットワークの例を以下に示します。

左側は元の画像、右側は圧縮後に復元された画像です。 3 x 3ピクセルのウィンドウを使用し、2番目のレイヤーのニューロン数は21、最大許容誤差は50でした。圧縮率は0.77でした。 ニューラルネットワークのトレーニングには129回の反復が必要でした。
ソースコードはここにあります (またはこちらはより高速なバージョンです)。