1)境界を強調、強化、強調する。
2)輪郭を自動的に作成します。
境界割り当ておよび非線形の既知の線形アルゴリズム。 線形フィルタリングで使用されるマスクと同様のマスクを最初のマスクとして引用できます。 違いは、正負両方の境界を強調するために異なる記号の重みが使用されることです。
たとえば、画像の水平または垂直処理(選択、増幅)のためのマスクの使用:
 そして
そして 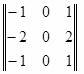
画像の単色領域では、すべてのポイントがほぼ同じ輝度を持ち、輝度レベルの勾配は低く、結果の画像では、そのような領域は単純に暗くなります。 違いがある場合(シャープトランジション、エッジ)、輝度の変化の急峻さが高く、そのような場所の最終画像に明るい線が表示されます。
別のオプションは、非線形アルゴリズムです。 これらには、ロバーツとソベルの開口部、シャーなどが含まれます。 アルゴリズムなど
ソーベル演算子
Sobelオペレーターは世界中でよく知られており、多くのタスクに使用されています。 Sobel演算子は、画像の勾配をより不正確に近似しますが、多くの問題で実際に使用するには十分な品質です。 より正確には、演算子は各ピクセルの3×3付近でのみ強度値を使用して対応する画像勾配の近似値を取得し、重み付き輝度係数の整数値のみを使用して勾配を推定します... [Sobel operator wiki]
Sobel演算子の式:
GxとGyは2つの行列であり、各点にはxとyに関する近似導関数が含まれます。 これらは、マトリックスGxとGyを乗算し、両方のマトリックスを合計することにより、次のように計算されます。その結果、結果は新しいイメージの現在のxおよびy座標に書き込まれます。
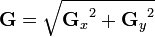
行列GyおよびGx:
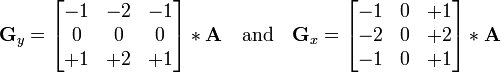
プレウィット演算子
Prewitt演算子のアルゴリズムは、異なる行列を使用することを除いて、Sobel演算子のアルゴリズムに似ています。
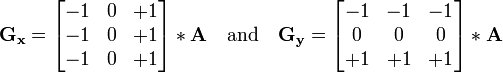
[Prewitt operator Wiki]
オペレーターシャラ
Sharr演算子aのアルゴリズムは、別の行列を使用することを除いて、Sobel演算子のアルゴリズムに似ています。

[オペレーターShcharra Wiki]
ロバーツクロスオペレーター
ロバーツのクロス演算子は、対角線方向に隣接するピクセル間の差の二乗和を計算する最も初期の境界抽出アルゴリズムの1つです。 これは、イメージを2つのコアで畳み込むことで実行できます。
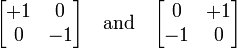
離散的な2次元微分演算を使用した結果、新しい値が取得され、新しい写真に記録されます。
[クロス演算子ロバーツ]
微分境界
この方法は、さまざまな勾配ベクトルの方向で2次導関数のゼロを検出するために微分アプローチを使用することから成ります。
マトリックスの係数の前にある係数を使用して、差を増減することが提案されました。 係数の範囲[0.1; 1.5]。 オペレーターの結果は、いくつかの写真で以下に示されています。
0.1、0.4、0.8、1.0、1.2、および1.5という名前の数字は、係数を使用したSobel演算子の結果です。
1.0に等しい係数の場合-ソーベル演算子。
ブレストショット

キャプチャ

シュレック

また、二値化のしきい値を適切に使用すると、非常に良い利益を達成できます。アイデアを持っている人なら誰でも聞いて(読んで)喜んでいるでしょう。