はじめに
プログラミングのモナドは世紀の謎になったようです。 そして、これには2つの理由があります:- カテゴリー理論の知識不足;
- 多くの著者はカテゴリーにまったく言及しないようにしています。
カテゴリーとファンクターの簡単な紹介から始め、次にモナドの定義、カテゴリー内のモナドの簡単な例、最後にプログラミング言語で使用されるモナドの用語を説明します。
モナドはカテゴリに関してほとんど初歩的であると確信しています。
内容
カテゴリー
カテゴリは、 オブジェクトとそれらの間の射で構成されます。 「モーフィズム」という用語は完全に正しいわけではありません(何かを変換する必要はありません)。したがって、しばしば、その抽象的な本質を示すために、モーフィズムは「矢印」と呼ばれます。すべての場合に「矢印」という用語を使用します。さらに、矢印が特定の機能を示す場合、「モーフィズム」と呼びますが、私にとっては依然として矢印のままです。
オブジェクトや矢印が何であれ、次のプロパティのみが重要です。
オブジェクト間に矢印が描画されます(この場合、オブジェクトは同じものにすることができます)。 これは次のように表されます。f:a→b 、ここでfは矢印、 aとbはオブジェクトです。
- 矢印f:a→bおよびg:b→cの場合 、 合成と呼ばれる矢印h: a→cが存在します: h = g°f 。

- 各オブジェクトaには、 単位矢印 、 id a :a→aがあり 、任意のf:a→bに対して次のことが当てはまります。
f°id a = fおよび任意のg:c→a id a °g = gです。 - 組成は連想的です: f°(g°h)=(f°g)°h
備考 このエントリの非常に抽象的な性質を考慮すると、「すべてのオブジェクト」または「aからbへのすべての矢印」がセットを形成することは期待できません。 セットであるカテゴリは、「小」または「局所的に小」と呼ばれます。
カテゴリーの例
「クラシック」カテゴリの例:- セットは、すべてのセットのカテゴリです。 オブジェクトはすべてセットであり、射はセットに対する関数です。
- Setfは、すべての有限集合とそれらの間の関数のカテゴリです。
- Relは、オブジェクトがすべてセットであるカテゴリであり、二項関係が射の役割を果たします。 構成は、内部結合によってマージされます。
- 部分は、すべての集合のカテゴリであり、射としての部分関数です。 XからYへの部分関数は、X o⊂XからYのサブセットからの関数です。
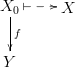
- Topは、すべてのトポロジ空間とそれらの間の連続関数のカテゴリです。
- どのグループもカテゴリと見なすことができます。要素のグループは、単一のオブジェクトの射です。
恒等関数は、グループの中立的な要素です。 そして、構成は乗算です。 - 部分的に順序付けられたセットは、カテゴリとして表すことができます。 セットの要素はオブジェクトです。 各ペアa、bに1つの矢印a→bを追加し、a <bおよびaごとに単位矢印a→aを追加します。
オブジェクトの各ペアには矢印が1つしかなく、半順序が推移的であるため、合成( a <b、b <c => a <c )があります。つまり、その結合性について心配することはできません。 - 前の例の特殊なケースとして、整数のセット[N ... M]はカテゴリと見なすことができます。
- パスを矢印と見なすと、任意の有向グラフをカテゴリに変換できます。 空のパスは単一の射であり、パスの連結は構成になります。
- オブジェクトとしての自然数、矢印としての行列。 マトリックスNxMは矢印N→Mになります。 行列乗算は合成の役割を果たし、単位行列NxNは単位矢印N→Nになります。
追加資料
カテゴリで同型を定義するだけです-それは反転を持つものです。 つまり、 f:a→bおよびg:b→aがあり、 f°g = id bおよびg°f = id aが満たされている場合です。 この定義は後で必要になります。 単相性とエピモルフィズムを定義することもできますが、これはやや複雑で、この記事の範囲外です。前章のオブジェクト[0 ... N]を覚えていますか? 特別なカテゴリがあります: 1 = [0]および2 = [0 ... 1] 。 最初は単一の射を持つ1つのオブジェクト、2番目は2つのオブジェクトと3つの射です。
カテゴリー自体がカテゴリーを形成していますか? はい。ただし、それらの間の矢印を定義する必要があります。 それらは二次矢印であり、ファンクターと呼ばれます。
ファンクター
ファンクターは、あるカテゴリーを別のカテゴリーにマップします。 これを行うには、最初のカテゴリから2番目にオブジェクトをマッピングし、最初のカテゴリから2番目のカテゴリの矢印に一貫した方法で矢印(射)をマッピングする必要があります。どのような一貫性が期待されますか? XとYを2つのカテゴリにします。 ファンクターFを定義します:X→Y オブジェクトをXからYにマッピングする必要があります。Xの各aにはYのオブジェクトF(a)があり、 Xの各矢印fにはYの矢印F(f)が必要です。
一貫性を保つために、次の規則に従う必要があります。
- f:a→bの場合、 F(f):F(a)→F(b) -ドメインとコードネームが保存されます。
- id a :a→a F(id a )= id F(a) :F(a)→F(a) -ユニットが保存されます。
- f:a→bおよびg:b→c F(g°f)= F(g)°F(f)の場合、組成は保持されます。
ファンクターの例
- カテゴリXのアイデンティティファンクタ。 アイデンティティX→Xはオブジェクトと矢印を変更せずに保持しますが、それでもファンクターです。
- Setf SetはSetにSetfを含むファンクターで、関数と同様に有限セットをそれ自体にマッピングします。 これは同一のファンクターではないことに注意してください。
- Set→Topは前の例と同様で、このファンクターはSetをTopの一部にします。 各セットは、離散トポロジ空間にマッピングされます。
- 任意のセットAに対して、次のファンクターを定義できます。
(-xA): セット → セット -任意のセットXをデカルト積X×Aにマッピングします。
- 任意のセットAに対して、ファンクタP Aを定義できます。 セット → セット 、これは任意のセットXをX Aにマップします— AからXへの関数のセット。
- セットパーツは、部分的な機能を持つセットにセットを導入します-セットとその中の機能を表示します。
- 項目6の逆は、ファンクター+ヌル: パーツ → セット -このファンクターは、各セットX↦(X +ヌル)に 「 ヌル拡張」を追加し、部分関数X→Yが関数(X +ヌル)→(Y + Null) 。
エクササイズ 。 部分関数に対して同じ拡張子を定義します。
小さなカテゴリとそのファンクタを見てみましょう。
- グループをカテゴリとすると、ファンクタはどうなりますか? ファンクターは、単一の形態と構成を維持する必要があります。 したがって、ファンクターはグループ準同型です。
- 2つの部分的に順序付けられたセット間の順序(いわゆるモノトーン)を保持する関数は、ファンクターです。
- 一対の指向グラフとエッジを保持するマップを取ります。 このマッピングを、あるグラフから別のグラフのパスにマッピングする関数に拡張できます。 この関数は、定義により、リンクと空のパスを保存するため、グラフによって作成されたあるカテゴリから別のカテゴリへのファンクタです。
- カテゴリー1を覚えていますか? それで、 1からカテゴリCまでのファンクターはどのように見えるでしょうか? 1にはオブジェクトが1つだけあり、同一の射があります。 したがって、このファンクターの定義は、 Cからオブジェクトを選択することと同じです。カテゴリCのオブジェクトXに対しては、ファンクターポイントXを定義できます: 1 → C
自然な変換
これは最も難しい部分でなければなりません。 2つのファンクターF、Gがあると仮定します: X → Y。 自然変換η:F→Gは 、各オブジェクトx∈XにYに矢印η(x):F(x)→G(x)があり、次のプロパティがある場合に定義されます。- すべてのf:a→bについて、等式が成り立ちます: G(f)°η(a)=η(b)°F(f) 。
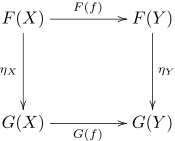
したがって、それは「自然」と呼ばれます-矢印上のファンクターの動作と一貫して動作します。
自然な変換の例
- ポイントファンクタを覚えていますか? したがって、カテゴリCに矢印f:a→bがある場合、この矢印は点aから点bへの自然な変換を定義します。 これは、ポイントファンクタトランスフォームとカテゴリ矢印の間の1対1の関係です。
- AとBの 2つのセットと関数fを取ります:A→B この関数は、ファンクター(-xA)、(-xB)間の自然な変換を定義します: Set → Set 。 (-xf):(-xA)→(-xB)次の式に従って: (x、a)↦(x、f(a)) 。
この定義は次の形式で記述できます。(define (cartesian f) (lambda (x a) (list x (f a))))
, :
(define (return x) (lambda (a) (x)))
C T: C → C : η: 1 → T μ: T ° T → T. T(η): T → T ° T , T η T(μ): (T ° T) ° T → T ° T.
:
- T(η) ° μ T → T
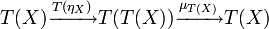
- T(μ) ° μ μ ° μ:
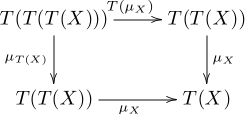
- C , .
- , G. MG Set. :
X ↦ X × G.
u(X): X → X × G x (x, e), e .
MG(MG(X)) = (idX, mG), mG . - Set. , List, X (x1, x2, x3...) X, . , u m. uX: X → List(X) x ∊ X mX: List(List(X)) → List(X) .
. , «computer science».
, - , , ?
( ) C: X → X , ∀ x ∊ X x <= C(x) C(C(x)) = C(x).
, , - , , - . - .
Part. A :
PlusNull: X ↦ (X+Null)
, Part Set. Set Part, .
? uX: X → (X+Null) mX: ((X+Null)+Null) → (X+Null).
, Null Null. Lisp :
(define (ux x) x)
(define (mx x) x)
Set. A :
X ↦ (X × A)A
A , , (X × A)A X X, A → (A × X), , X.
? uX: X → (A × X)A x ∊ X , A x X.
Lisp:
(define (ux x)
(lambda (a) (list a x)))
mX: (A × (A × X)A)A → (A × X)A?
mX: (A × (A × X)A)A, A , ( A , X ). , , A?
Lisp:
(define (mx f)
(let (tr1 out1)
((car f) (cadr f))) ; f: A → (A × (A × X))^A
(lambda (a)
(let a1 (tr1 a)) ;
(let f2 (out1 a)) ;
(let (tr2 out2) ((car f2) (cadr f2))) ;
(list (tr2 a1) (out2 a1))))
. , .
, f: X → Y, X «», Y «».
, ; , 100% , . , « » .
, , .
NullObject NaN.
, X, (Y+Null), .
, , .
IO Haskell
Haskell IO, , .. , . , A , , X .
. A String, «», «».
, , getc, , , putc, .
, .
- .
- , , .
- “Comprehending Monads” Frederik Eaton — .
- Haskell u return, m join
- Haskell List .
- map/reduce Google.