ゲームのルール
カードのデッキは慎重にシャッフルされ、2人のプレイヤーに均等に配られます(各18枚のカード)。 プレイヤーは同時に一番上のカードを引き、それを持っている人は両方を取りますが、6人はエースよりも高いと見なされます。 カードが等しい場合、両方のプレイヤーがもう1枚のカードを引いて(存在する場合)、それらを閉じたカードに入れ、その後、彼らはさらにもう1枚のカードを引き出して比較します。別の反復が実行されます。
テーブルからのカードはデッキの底の下に置かれ、同時にシャッフルされることが重要です(ループの可能性を排除するため)。
カードの配布
プログラムの実装中に、6からエースのカードと呼ばれる、0から8の数字を持つカードと呼ばれるカードから可能な限り抽象化しようとしました。スーツは完全に無視されました。 テスト結果は、取引の質に大きく依存します-プレーヤーのデッキのカードがどれくらいランダムであるかに依存します)。 ただし、慎重にシャッフルしても絶対的なランダム性は保証されないため、プログラムで何も発明しなかったので、デッキからランダムに選択したカードを1000回交換しました。
void generateMap(QList* player1, QList* player2)
{
int a[36];
for ( int i = 0; i < 36; i++)
a[i] = i / 4;
int temp, i1, i2;
for ( int i = 0; i < 1000; i++)
{
i1 = random() % 36;
i2 = random() % 36;
temp = a[i1];
a[i1] = a[i2];
a[i2] = temp;
}
for ( int i = 0; i < 18; i++)
{
player1->append(a[i]);
player2->append(a[i+18]);
}
}
ゲームプレイ
アルゴリズムは、誰もがカードを持っている間、両方のプレイヤーがゲームの繰り返しを繰り返すというものです。誰かが手にカードを持ち、競合がある場合(両方のカードが同じで、移動がまだ行われていない)、プレイヤー、可能であれば、彼らは1-2枚のカードを捨て、額面で判断して、誰がすべてのカードを捨ててテーブルに置くかを決定します...
int Process(QList* player1, QList* player2)
{
QList* temp = new QList();
int p1, p2, k;
int counter = 0;
while ((player1->count() > 0) && (player2->count() > 0))
{
p1 = -1; p2 = -1;
while ((p1 == p2) && ((player1->count() > 0) || (player2->count() > 0)))
{
for ( int i = 0; i < 1 + (p1 >= 0); i++)
if (player1->count() > 0) {
p1 = player1->first();
temp->append(p1);
player1->removeFirst();
}
for ( int i = 0; i < 1 + (p2 >= 0); i++)
if (player2->count() > 0) {
p2 = player2->first();
temp->append(player2->first());
player2->removeFirst();
}
}
QList* winner;
if ((p1 > p2) || ((p1 == 0) && (p2 == 8))) {
winner = player1;
} else {
winner = player2;
}
while (!temp->isEmpty())
{
k = random() % temp->count();
winner->append(temp->at(k));
temp->removeAt(k);
}
temp->clear(); counter++;
if (counter > 100000) player1->clear();
}
delete temp;
return counter;
}
結果表示
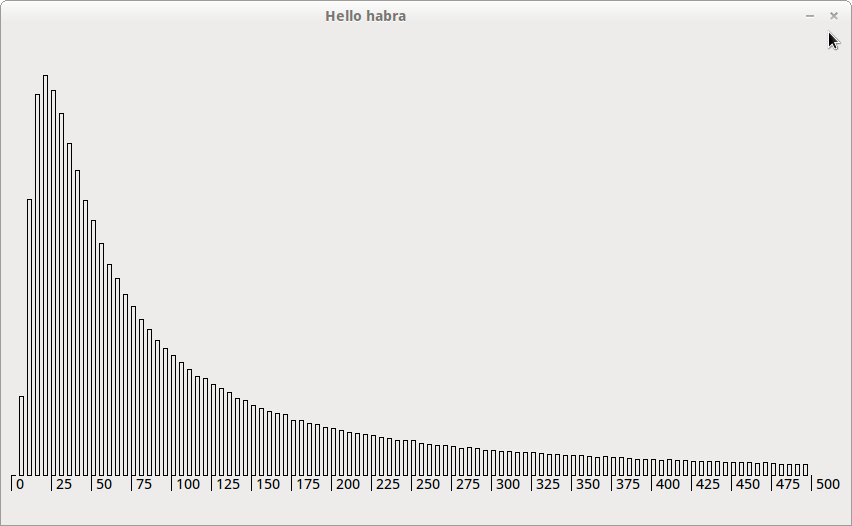
グラフは、ゲームを完了するために必要な動きの数のランダム変数の確率密度を示しています。
void CChart::paintEvent(QPaintEvent *){
QPainter painter( this );
for ( int i = 0; i < 21; i++) {
painter.drawText(QRect(i*40+15,450,30,20),QString::number(i*25));
painter.drawLine(10+i*40, 465, 10+i*40,450);
}
for ( int i = 0; i < 100; i++){
int h = this ->counts[i] * 400 / this ->max;
painter.drawRect(10 + i*8, 450-h, 4, h);
}
}
結論
E8400は100秒で1つのスレッドで1,000,000回の試行を完了しました。 スケジュールは私をとても驚かせました、それはゲームのほとんどが25手で終わることがわかりました。 そして時々さらに...しかし、マットの計算の結果を見ています。 期待と分散、落ち着いて、すべてが順調です:
マット予想:Mx = 255.054;
分散:Dx = 319726.545;
マットによって判断される合計。 あなたがこのゲームをプレイするために取る場合、30分でカウントします。そして、あなたがこのゲームをプレイするために取る場合、差異から判断して、何かに頼ることさえ考えないでください)。
更新する
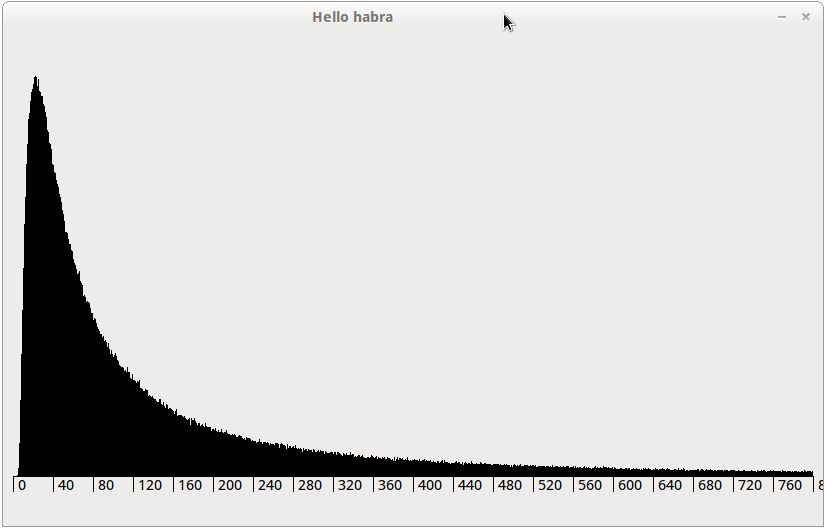
もう少し詳細な密度チャート。
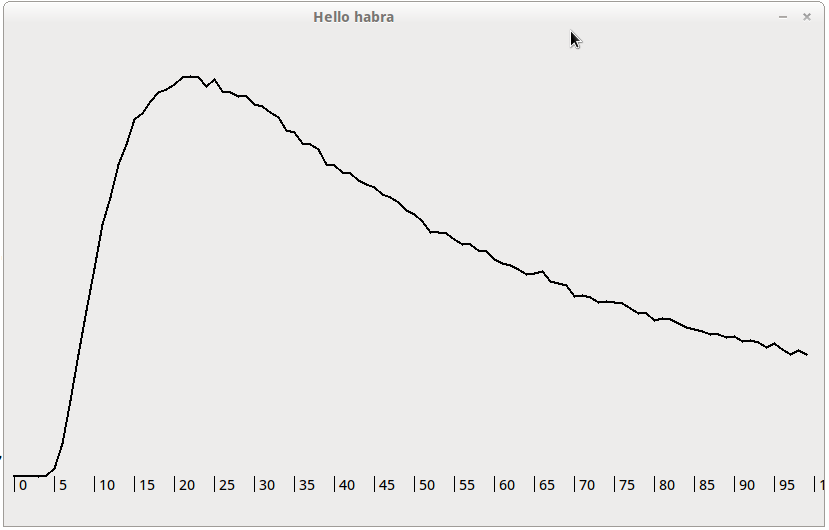
「本体」の「増加」。

OLSの要求に応じたLN(f)
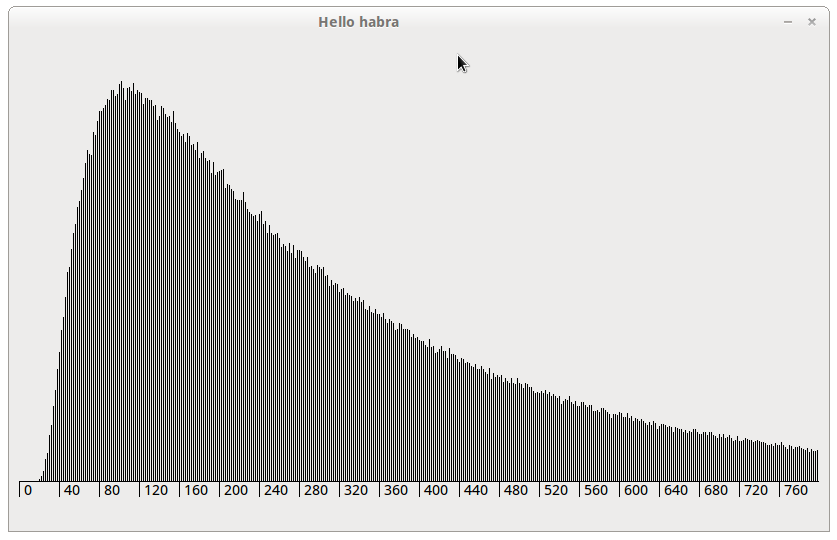
ゲームの連続バージョン(カードは0..1の数字)では、違いは分布パラメーターのみであり、すべてのペアになっていないxについてf(x)= 0です。 ボディグリムの要請により作成
さらにいくつかのプロパティ:
中央値:90;
ファッション:25;
信頼区間:80%-6〜316。
更新2
申し訳ありませんが、コードは結果を大きく歪めるいくつかの迷惑なエラーを見つけました。 この更新はn回再チェックされます 。テストの正確性は、 こちら 、 こちら 、 こちらで確認できます 。

最終結果:
マット 期待: 187 ;
分散: 23044 ;
中央値: 142 ;
ファッション: 62 。
C1-行われた移動の数。
c2-いずれかのプレイヤーのカードの数(それぞれがペアまたはペアでないカードの数を同時に持っています)。
唯一無二の状況が、ペアになっていない動きでゲームを完了させます-プレイヤーの1人がカードのペアを選択すると、ゲームが完了します。 これは、ゲームの終了時にのみ発生する可能性があります( 例) 。
改めておlogび申し上げます。 エラーを指摘してくれてありがとう