1972年、IBMのスーパープログラマーであるHarlan Millsは、プログラムのエラー数を推定するために次の方法を提案しました。 プログラムを作ってみましょう。 N個のエラーがあるとします。 私たちはそれらを自然と呼びます。 追加のM 人為的エラーを導入します。 プログラムをテストしましょう。 テスト中にn個の自然エラーとm個の人為的エラーが検出されるようにします。 検出の確率は、自然エラーと人為的エラーで同じであると仮定します。 その後、関係が満たされます。
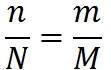
同じ割合の自然および人為的エラーが見つかりました。 したがって、プログラム内のエラーの数:

検出されないエラーの数は(Nn)です。
たとえば、20の人為的エラーをプログラムに導入すると、テスト中に12の人為的エラーと7つの自然的エラーが検出されました。 プログラムのエラー数の次の推定値を取得します。

検出されないエラーの数は(Nn)= 12-7 = 5です。
上記のミル法には重大な欠点があることがわかります。 100%の人為的エラーが見つかった場合、これは100%の自然なエラーが見つかったことを意味します。 しかし、人為的なミスを少なくすればするほど、それらすべてを見つける可能性が高くなります。 唯一の人為的エラーを紹介し、それを見つけ、これに基づいてすべての自然なエラーを発見したことを発表します! この問題を解決するために、ミルズはNの値の仮説をテストするために設計されたモデルの2番目の部分を追加しました。
プログラムにN個の自然エラーがあると仮定します。 M人為的なエラーを導入します。 すべての人為的エラーが見つかるまで、プログラムをテストします。 この瞬間までにn個の自然エラーが見つかったとします。 これらの数値に基づいて、 Cの値を計算します。
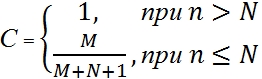
Cの値は、モデルの信頼性の尺度を表します。 これは、モデルが誤った仮定を正しく拒否する可能性です。 たとえば、プログラムに自然なエラーがないことを考えてみましょう(N = 0)。 プログラムに4つの人為的エラーを導入します。 すべての人為的エラーが見つかるまで、プログラムをテストします。 単一の自然エラーが見つからないとします。 この場合、(プログラムにエラーがないという)仮定の信頼度は80%(4 /(4 + 0 + 1))になります。 これを90%にするには、人為的エラーの数を9に増やす必要があります。自然なエラーがないという次の5%の信頼度は、10個の追加の人為的エラーになります。 Mは19にする必要があります。
プログラムに3つ以下の自然誤差(N = 3)があると仮定した場合、6つの人為的エラー(M = 6)を追加し、すべての人為的エラーと、1つ、2つ、または3つ(しかしもう!)モデルの信頼度は60%(6 /(6 + 3 + 1))になります。
NおよびMのさまざまな値に対する関数Cの値(パーセント):
表1-1ずつ増加。
表 2-5の増分。
信頼度の計算式から、結果の推定値に必要な信頼度を得るためにプログラムに入力する必要がある人為的エラーの数を計算する式を簡単に取得できます。

Nのさまざまな値に対して目的の信頼度を達成するためにプログラムに導入する必要がある人為的エラーの数:
表3-1ずつ増加。
表 4-5の増分。
Millsモデルは非常に単純です。 その弱点は、エラーを見つける可能性が等しいという仮定です。 この仮定を正当化するために、人為的エラーを導入する手順には、ある程度の「インテリジェンス」が必要です。 もう1つの弱点は、 すべての人為的エラーを確実に見つけるためのMillsモデルの2番目の部分の要件です。 そして、これは長い間起こらないかもしれません。