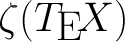TeX-wayの数論

TeXに数論関数計算機を組み込むことにより、TeXマクロを記述するいくつかの機能を示します。

問題の声明

時々、別のテキストを入力する必要があります。それには、数論関数の計算例が含まれます。 オイラー関数φ 、 除数関数τ 、 カーマイケル関数λです。 以前は、これは次のように行われていました。お気に入りの電卓（私の選択はPARI / GP ）を実行し、その中のすべてをカウントし、計算をTeXにコピーします。 初期データが変更されました-再び計算機に、またはその逆。 多くの大騒ぎ、ある種の中間結果を置き換えることを忘れる多くの機会。 そして、マウスで退屈しました。 最も一般的な機能であっても、このプロセスを自動化して、

$\phi(1001)=\Phi(1001)$
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

印刷される





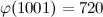
最も一般的な解決策は、外部プリプロセッサを使用することです。これは、数式の必要なフラグメントを噛み、それらを外部計算機に渡し、結果を取得してドキュメントに貼り付けます。 主な欠点は、もちろん、互換性の損失です。 以前は、メールでtexファイルを転送するだけでした。 さて、もう一方の端でpdfにコンパイルできるように、必要なプリプロセッサと計算機を示す詳細な指示も必要です。 この段階では、受信者が別のOSやタンバリンとのダンスを必要としないことがほぼ確実にわかります。 プランBに進みます。

プランb

TeX独自の手段で取得してみましょう。ご存知のように、そのマクロはチューリング完全言語を構成します。 Brainfuckほど難解ではありませんが、Cライクな構文や、さらに悪いことにセマンティクスからはほど遠いものです。



最初に注意することは、マクロは引数を取ることができますが、値を透過的に返すことはできないということです。 パスカリストは、マクロは関数としてではなく、手続きとして振る舞うと言うでしょう。 たとえば、2つの数値を合計するマクロを作成する方法は次のとおりです。

 \newcount\s\def\addition#1#2{\s=#1\advance\s by#2 \number\s}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

混乱した？ コメントとスペースのみでもう一度試してみましょう。

 \newcount\s %    \def\addition#1#2{ %      \s=#1 %   s   \advance\s by#2 %    \number\s %    }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

いま

 2+3=\addition{2}{3}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

「2 + 3 = 5」という印刷が得られます。



（ 数学関数のさらにいくつかの例 ）

部門全体

もっと複雑なものを書きましょう。 私たちの最初の目標は、ある数値が別の数値で割り切れるかどうかをチェックする関数です。

 \newif\ifdivisible %    \newcount\testMod@n %    \def\testMod#1#2{ %      \testMod@n=#1 %   testMod@n   \divide\testMod@n by#2 %      \multiply\testMod@n by#2 %      \ifnum#1=\testMod@n %       , \divisibletrue %    , \else %   \divisiblefalse %  \fi% }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このマクロは、除算が余りなく通過した場合は割り切れるtrueを、そうでない場合はfalseを置きます。 私たちはチェックします：

 \testMod{6}{3} \ifdivisible 1 \else 0 \fi \testMod{6}{4} \ifdivisible 1 \else 0 \fi
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

出力は「1 0」になります。6は3で除算されますが、4で除算されません。



このコードをファイルに保存し、 texを使用して収集した場合、「TeX容量を超えました」というエラーがすでに表示されている可能性があります。 実際には、マクロや変数の名前で有効な通常の文字と見なされるように@を求めるのを忘れていました。 次のコマンドでこれを行うことができます

 \catcode `\@11
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

（これは、LaTeXがエイリアス\ makeatletterで使用しているものと同じマクロです。）



一般に、TeXは変数とマクロのスコープで動作できますが、通常のプログラミング言語で通常行われているものとは大きく異なります。 たとえば、

 \def\addition{\newcount\s}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

マクロ内で変数を宣言すると失敗します：「\ aの定義をスキャン中に禁止された制御シーケンスが見つかりました」。 いくつかの回避策が考えられますが、「ローカル」（実際にはグローバル）変数に<関数名> @ <個人名>という名前を付けて、すっきり（！）にすることに同意すれば十分です。 すべてのマクロ定義の後、再び@を特殊文字で作成します

 \catcode `\@12
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これにより、後のドキュメントからこれらの変数に直接アクセスできなくなります。



コードテスト\ testMod

ユニタリ除数とべき乗

次のステップ：1つの数値の最大次数を計算するマクロを作成します。これは、もう一方の整数を分割します（ dが素数の場合、これはユニタリ除数です ）。

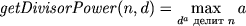
 \newcount\divisorpower %      , \newcount\getDivisorPower@m %   - n/d^a \def\getDivisorPower#1#2{ \getDivisorPower@m=#1 %   \divisorpower=0 % \testMod{\getDivisorPower@m}{#2} % ,    d \loop\ifdivisible % while-,   divisible \advance\divisorpower by1 %  a  1 \divide\getDivisorPower@m by#2 %   d \testMod{\getDivisorPower@m}{#2} %  ,    d \repeat %     }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Cでは、このコードは次のようになります（意図的に不器用に記述しています）。

 int divisible; int a; int m; void getDivisorPower(int n, int d){ m = n; a = 0; divisible = (m % d == 0); while(divisible){ a++; m /= d; divisible = (m % d == 0); } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

今、完全に軽いマクロ：

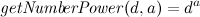
 \newcount\numberpower %        \newcount\getNumberPower@pow %   -      \def\getNumberPower#1#2{ \numberpower=1 %   \getNumberPower@pow=#2 \loop\ifnum\getNumberPower@pow>0 %   \multiply\numberpower by#1 \advance\getNumberPower@pow by-1 \repeat }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

再びCで：

 int numberpower; int pow; void getNumberPower(int d, int a){ numberpower = 1; pow = a; while(pow > 0){ numberpower *= d; pow--; } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

より効率的なべき乗アルゴリズムを実装することもできますが、これで十分です。



チェックを行う時間です：

 \getDivisorPower{600}{2} \number\divisorpower \getDivisorPower{600}{3} \number\divisorpower \getDivisorPower{600}{5} \number\divisorpower \getDivisorPower{600}{7} \number\divisorpower
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

「3 1 2 0」を出力する必要があります。

 \getNumberPower{5}{0} \number\numberpower \getNumberPower{6}{1} \number\numberpower \getNumberPower{7}{2} \number\numberpower
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

「1 6 49」が得られます。



コードテスト\ getDivisorPowerおよび\ getNumberPower

次は？

パート2では 、オイラー関数を考慮するマクロを作成します。 最もせっかちな人のために- マクロの作業バージョン 。 TeXはn〜10 ⁹での計算に簡単に対応します。



第3部では、TeXでの数学計算のさらに洗練された例と、もちろんベンチマークがあります。