外部輪郭を使用して画像にすばやくマークを付ける

記事では、バイナリラスタ上の接続オブジェクトをすばやくリストする方法を説明します。 このアルゴリズムを画像とテキストの認識に使用しました。 処理速度が速い（最大3200x2400までの写真で、一部の予約ではミリ秒で解決する）ことと理解しやすいこと（C ++の知識があること）で類似のものとは異なります。 元の画像はアルゴリズムによって「読み取り専用」として解釈されることに注意してください（他の方法で処理できるものを台無しにする理由）。これに関連して、アルゴリズムには少量の追加メモリが必要です。 さらに、外側の輪郭は、画像の分析とベクトル化に役立つオブジェクトです。





そのため、タスク：元の画像（画像ポイントの配列）をアウトラインのリストに変換します。 パスは、画像の接続部分の外部ポイントのセットです。 たとえば、塗りつぶされた円の輪郭は、すべての外部ポイントから取得された円です。



8つの連結性が使用されます。つまり、2つのポイントが、上下左右方向および対角線上で隣接している場合、それらが接続されます。 したがって、各ポイントには最大8つの隣接ノードを含めることができます。

ちょっとした準備

次の構造を使用して、オブジェクトの指定された初期外部ポイントから非常に効率的に輪郭を取得するアルゴリズムの構築を開始します。

class Contour : public Points

{

// references to the constructor params

const Image& SourceImage;

ImageMap& CurrentImageMap;



public :

/* here we assume that image is coherent in any of 8 ways,

* so if the pixel will not have neighbor in any of 4 diagonal and 4 straight directions

* then it will be considered as separate image part */



// extract contour and mark all coherent points on image map

Contour( const Image& img, ImageMap& map, const Point& start);



private :

// private methods for contour pass implementation only

void passDownLeft(Point& p, bool InvertedAxis = false );

Point movePoint( const Point& src, int x, int y, bool InvertedAxis = false );

Point commitPoint( const Point& p);

};

以下に、検討する必要のあるすべてのオブジェクトとメソッドを示します。 コンストラクターは間違いなくSourceImageです。



ImageMapとは何ですか？ 実際、輪郭を構築するためのアルゴリズムは、それらの繰り返しの訪問を防ぐために、何らかの方法でポイントをマークする必要があります。したがって、考慮されるポイントは、それらが属するオブジェクトの番号でマークされます。



これには、元の画像が占有するメモリと同じ量のメモリが必要と思われますが、より効率的な構造を使用します。 輪郭に属さない、または輪郭内にあるポイントにメモリを浪費することは意味がないので、小さなオーバーヘッドで境界ポイントのみを保存し、それらにすばやく対処できるようにします。





この構造は、STEP ²サイズの画像ブロックのインデックスに基づいています。 インデックス自体は、サイズX / STEP * Y / STEPのブロックへのリンクの配列です。XとYは元の画像の解像度です。 書き込みのためにブロックにアクセスすると、そのブロックはメモリに割り当てられ、対応するインデックス要素がそのポインターでマークされます。 最悪のシナリオでは、各（n * STEP、m * STEP）ポイントがマークされている場合、画像のサイズに等しいメモリ使用量を取得しますが、平均してメモリの50〜90％を節約します。 ご想像のとおり、インデックス付けは単に座標をSTEPで除算することで行われます。STEPが2の累乗の場合、これは非常に高速に機能します。



ところで、アルゴリズムを実行した後、ImageMapは画像上のオブジェクトをリストするタスクの結果です。



commitPointメソッドを使用して、輪郭にポイントを追加し、ImageMapを現在の輪郭に関連付けます。

Point Contour::commitPoint( const Point& p)

{

if (!CurrentImageMap.isAssigned(p) && SourceImage.isFilled(p))

{

CurrentImageMap.assignSegment(p, this );

push_back(p);

}

return p;

}



もちろん、これらは実装の詳細ですが、ここではすべてがシンプルで再利用できます。 movePoint関数も非常にシンプルで、指定された増分をポイントに追加するだけです。

Point Contour::movePoint( const Point& src, int x, int y, bool InvertedAxis)

{

Point p = src;

if (InvertedAxis)

{

x = -x;

y = -y;

}

pX += x;

pY += y;

return p;

}



InvertedAxisパラメーターは、ご想像のとおり、増分を反対に変更するだけです（これは後で便利になります）。

アルゴリズムコア

さて、今面白い。 実際には、バイパス関数自体：passDownLeft。 与えられた開始点に対して、 可能であれば 、オブジェクトを下に向かって左に移動します 。



オブジェクト内にいる間（つまり、現在のポイントの色は背景色と等しくありません）：

• 現在のポイントに対して1ポイント下に行きましょう。
• 左のポイントが、新しい現在のポイントに対して満たされている場合、幸運なことに、「ストップまで」左に移動します。 左端のポイントの上のポイントがいっぱいになったら、自己交差点を見つけて迂回を終了します。
• 塗りつぶされていない場合は、塗りつぶされたポイントに到達するまで右に移動します。

単純に聞こえますが、正確な実装はもう少し複雑に見えます。

void Contour::passDownLeft(Point& p, bool InvertedAxis)

{

while (SourceImage.isInside(p))

{

commitPoint(p);



// step one point down

p = movePoint(p, 0,1, InvertedAxis);



// select one of neighbors which is filled, prefer left one...

Point left = movePoint(p, -1,0, InvertedAxis);

if (SourceImage.isFilled(left))

{

p = commitPoint(left);

// ...and shift left as many as possible

while (SourceImage.isInside(p))

{

Point left = movePoint(p, -1,0, InvertedAxis);

if (!SourceImage.isFilled(left))

break ; // no more left neighbors



p = commitPoint(left);



Point up = movePoint(p, 0,-1, InvertedAxis);

if (SourceImage.isFilled(up))

return ; // crossed inside area

}

}

else

{

// selection still unfilled...

while (SourceImage.isInside(p) && !SourceImage.isFilled(p))

{

// ...shift right by connected points and test again

Point right = movePoint(p, 1,0, InvertedAxis);

Point rightUp = movePoint(right, 0,-1, InvertedAxis);

if (!SourceImage.isFilled(rightUp))

return ; // no more bottom right neighbors

commitPoint(rightUp);

p = commitPoint(right);

}

}

}

}

isInside関数は、境界を越えないように、ポイントが画像内にあるかどうかをチェックします。



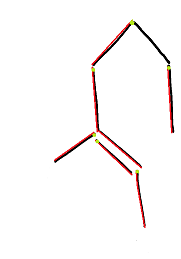テスト画像上でこのバイパスを起動すると（各オブジェクトをバイパスするための開始点は薄緑色のポイントです）、構築プロセスは各オブジェクトの最低点に基づいているため、輪郭は得られません。 したがって、そのような機能の1つでは不十分です。 ただし、この場合に提供されるInvertedAxisフラグを使用して簡単に取得できるので、上下に移動することで輪郭を補足できます！ したがって、最後に特別に残されたコンストラクターは、輪郭構築アルゴリズムに追加されます。

ontour::Contour( const Image& img, ImageMap& map, const Point& start)

: SourceImage(img), CurrentImageMap(map)

{

bool doneSomething = true ;

Point p = start;

for ( int iter = 0; doneSomething; iter++)

{

size_t count = size();

passDownLeft(p, iter % 2 == 1);

doneSomething = size() > count;

}

}



これにより、新しいポイントがパスに追加されるまで、左下と右上のラウンドが交互に行われます。



したがって、特定の画像オブジェクトの外部輪郭のすべての点をリストする作業方法があり、この輪郭の点の数に対して線形時間で作業します。

開始点の列挙

残っているのは、ソースイメージから輪郭を作成するためのすべての開始点を見つけることだけです。

void Vectorization::getContours()

{

Point p(0,0); // line-by-line scan to extract contours of objects

for (pY = 0; pY < SourceImage.getHeight(); p.Y++)

{

for (pX = 0; pX < SourceImage.getWidth(); p.X++)

{

if (SourceImage.isFilled(p) && !ImageMap.isAssigned(p))

{

// that pixel is unprocessed yet, so extract the contour starting from it

Contour* c = new Contour(SourceImage, ImageMap, p);

// add new contour

ContoursStorage.push_back( c );

}

}

}

}

これまでのところ、これはアルゴリズムの最も遅い部分です。結局のところ、画像のすべてのポイントを回る必要があります。



しかし、その最適化も実際には表面上にあります。ImageMapを保存するときと同じインデックス構造を使用し、イメージをサイズSTEP ^2のブロックに分割します。

void Vectorization::getContoursOptimized()

{

Point pIndex(0,0); // step-by-step scan

for (pIndex.Y = 0; pIndex.Y < SourceImage.getHeight(); pIndex.Y += STEP)

{

for (pIndex.X = 0; pIndex.X < SourceImage.getWidth(); pIndex.X += STEP)

{

if (!SourceImage.isEmptyIndex(pIndex))

{

Point pLocal = pIndex;

for (pLocal.Y = pIndex.Y ; pLocal.Y < STEP; pLocal.Y++)

{

for (pLocal.X = pIndex.X ; pLocal.X < STEP; pLocal.X++)

{

if (SourceImage.isFilled(pLocal))

{

if (Map.isAssigned(pLocal))

{

pLocal.X = dynamic_cast<Contour*>(Map.getSegment(pLocal))->getMaxX(pLocal.Y);

break ; /* skip already processed points by getting the max contour X for the specified Y */

}

// that pixel is unprocessed yet, so extract the contour starting from it

Contour* cntr = new Contour(SourceImage, Map, pLocal);

// add new contour

ContoursStorage.push_back( cntr ) ;

}

}

}

}

}

}

}

このアルゴリズムの複雑さは、画像オブジェクトの外部輪郭の点の数に比例します。

キャッチ

最後の事実から、この方法は、接続されたポイントのグループが実質的にない画像では一般的にあまり良くありませんが、ポイントで塗りつぶすことは可能な限り完全に近いです（25％-各座標ごとに2番目のポイントが塗りつぶされ、残りは-いいえ）。



しかし、画像処理の問題の観点からすると、そのような写真は単なるノイズであり、予備フィルターによって簡単にカットされます。 だから、すべてがうまくあります:)