問題の声明
長さNの配列Aが与えられ、数値K≤Nが与えられたとしましょう。この配列の長さKのサブセグメントで最大(最小、合計...)を見つける必要があります。 これはRMQ問題(範囲最小クエリ)の特殊なケースですが、追加の制限があり、検索セグメントの長さが一定です。 このソリューションでは、タスクは配列の要素を変更する可能性を意味しません。 明確にするために、最大値を見つけることを検討します。
長所と短所
このアルゴリズムでは、O(N)の前処理を使用して、O(1)の固定長サブセグメントの最大値を見つけることができます。 この場合、補助メモリには2 * Nが必要です。 しかし、主な利点は、非常に単純な実装と理解可能性と考えることができます。 欠点は、アルゴリズムが元の配列の要素を変更するように適合されていないことです。 つまり 変更は可能ですが、このためには、O(K)アクションの順序を実行する必要があります。
解決策
前処理
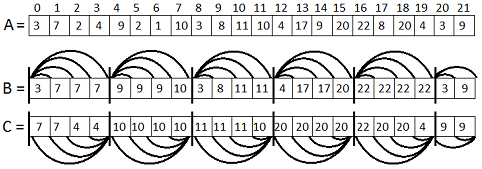
元の配列Aを長さK-1のブロックに分割します(K-1が少し低いと理解する理由)。 次に、2つの追加配列BとCを次のように計算します。
B [i]には、現在のブロックの先頭からi番目の要素までの間隔の最大値が格納されます。
C [i]では、i番目の要素から現在のブロックの最後までの間隔の最大値を格納します。
たとえば、B [2]ではA [0]からA [2]までの最大値を保存し、C [2]ではA [2]からA [3]までの最大値を保存します。 この操作はO(n)で実行できることは明らかです。 次の図は、N = 22、K = 5の例を示しています。
リクエスト処理
さて、この単純な構造の助けを借りて、長さKのセグメントの最大値を簡単に見つけることができます。クエリのエッジが常に2つの隣接するブロックに収まるように、長さK-1のブロックを作成しました。 したがって、要求があると、境界線には2ブロックの境界線が含まれます。 これをTと呼びます。セグメントの左端はlで、右端はrです。 ここで、最大値を取得するには、最大値(C [l]、B [r])を取得するだけです。 実際、C [l]はlからTまでの区間の最大値であり、B [r]はTからrまでの最大値です。したがって、C [l]およびB [r]の最大値はlからtまでの区間で最大になりますr。
実装
以下は、C ++での最も単純な実装です。
vector< int > B, C; void build(const vector< int > A, int k) { int n = A.size(); B.resize(n); C.resize(n); k--; // B for(int i = 0; i < n; i++) { if(i % k) B[i] = max(A[i], B[i - 1]); else B[i] = A[i]; } // C C.back() = A.back(); for(int i = n - 2; i >= 0; i--) { if((i + 1) % k) C[i] = max(A[i], C[i + 1]); else C[i] = A[i]; } } int GetMax(int l, int k) { return max(C[l], B[l + k - 1]); }
適切な操作のためには、buildおよびGetMax関数の入力に供給されるKが同じであることも必要です。
明らかに、ビルド関数のこの実装は最適ではありませんが、最も単純で簡単です。 次の各ステップで、前の値に基づいて新しい値が計算されます。 以下は、より高速な実装です。
void build(const vector< int > A, int k) { int n = A.size(); B.resize(n); C.resize(n); B.front() = A.front(); C.back() = A.back(); k--; for(int i1(1), i2(n - 2); i1 < n; i1++, i2--) { B[i1] = (i1 % k) ? max(A[i1], B[i1 - 1]) : A[i1]; C[i2] = ((i2 + 1) % k) ? max(A[i2], C[i2 + 1]) : A[i2]; } }
まとめ
ご覧のとおり、アルゴリズムは実装と理解の両方の点で非常に単純です。 与えられた長さのサブセグメントの最大値を見つけるために、O(1)の漸近的に良い推定値を与えます。 この構造は、最小値または量を見つけるために簡単に変更できます。 さらに、可能なオプションの最大数はNKと等しくなります。つまり、この構造を使用すると、可能なすべての組み合わせをO(n)として計算できます。 各瞬間に、長さKの2つの隣接ブロックのみをメモリに保存する必要があります。これにより、より高度な実装でメモリサイズが削減されます。
アルゴリズムの作成者はVan Herkに属します。
参照資料
RMQチャレンジ-1.静的RMQ
RMQ問題-2.ラインツリー
スタックの変更による同じ問題の解決策(e-maxx)
RMQ(e-maxx)についてもう少し
大量の情報(英語)